Análisis Hidrodinámico de las Diferentes Posiciones del Dedo Pulgar en Natación
Victor Machado Reis2,3, António José Silva2,3, Abel Rouboa3, Daniel Almeida Marinho1,2,3, Francisco B Alves4, João P Vilas-Boas5 y Leandro Machado5
1University of Beira Interior. Department of Sport Sciences, UBI, Covilha, Portugal.
2Centre of Research in Sports, Health and Human Development, CIDESD, Vila Real, Portugal.
3University of Trás-os-Montes and Alto Douro. Department of Sport Sciences, UTAD, Vila Real, Portugal.
4Technical University of Lisbon. Faculty of Human Kinetics, FMH-UTL, Lisbon, Portugal.
5University of Porto, Faculty of Sport (FADEUP), Porto, Portugal.
Artículo publicado en el journal PubliCE del año 2010.
Publicado 31 de agosto de 2009
Resumen
Palabras clave: dinámica de fluidos computada, ingeniería reversa, mano, dedo, arrastre, elevación
INTRODUCCION
En la actualidad la técnica de simulación numérica es una de las herramientas numéricas más reconocidas en el campo de la ingeniería biomecánica. Esta metodología se ha utilizado en el análisis computado del flujo de fluidos en varios campos de investigación, tales como la medicina, la biología, la industria y el deporte (por ejemplo, Boulding et al., 2002; Dabnichki y Avital, 2006; Guerra et al., 2007; Marshall et al., 2004). Esta herramienta numérica es una rama de la mecánica de fluidos que resuelve y analiza problemas que implican un flujo de fluidos por medio de simulaciones mediante una computadora. Por lo tanto, uno de los beneficios más importantes es que responde con rapidez muchas preguntas que implican suposiciones. Es posible evaluar muchas variantes para buscar un resultado óptimo, sin una prueba experimental con seres humanos. Por medio de una computadora el usuario puede crear un modelo de cualquier campo de flujo, siempre que se conozca la geometría del objeto y se prescriban algunas condiciones iniciales del flujo. Esto puede proporcionar respuestas e información útil acerca de problemas que no se han podido determinar ni resolver con costos muy elevados (utilizando técnicas de evaluación físicas o experimentales). Así, se puede considerar que las técnicas de simulación numérica llenan el vacío entre la dinámica de fluido teórica y la experimental.
En el ámbito del deporte, los resultados más importantes sugieren que el análisis numérico podía brindar información útil acerca del rendimiento. De hecho, la utilización de las técnicas de simulación numérica ha producido mejoras significativas en el diseño de equipos y prescripción técnica en áreas como la práctica de navegación a vela (Pallis et al., 2000), carreras de Formula 1 (Kellar et al., 1999) y deportes de invierno (Dabnichki y Avital, 2006). En la natación, esta metodología se ha utilizado para el estudio de las fuerzas de propulsión producidas por la mano y el antebrazo al nadar (Bixler y Schloder, 1996; Gardano y Dabnichki, 2006; Lecrivain et al., 2008; Marinho et al., 2009a; Rouboa et al., 2006; Silva et al., 2005) y la magnitud de las fuerzas de arrastre que se oponen al movimiento hacia adelante (Marinho et al., 2008a; Silva et al., 2008; Zaidi et al., 2008). No obstante, aún existe una debilidad común: prácticamente todos los modelos que se han desarrollado se basan en representaciones analíticas aproximadas de las estructuras humanas y nunca se ha discutido sobre su precisión geométrica. Este método se ha adoptado con frecuencia, por ejemplo, para reducir el coste computacional de requerimientos de memoria (Aritan et al., 1997). Una de las razones más importantes de estas limitaciones es la dificultad de diseñar un auténtico modelo digital de las extremidades humanas. En la mayoría de los casos, los autores utilizaron modelos en dos dimensiones (Bixler y Schloder, 1996; Rouboa et al., 2006; Silva et al., 2005; 2008; Zaidi et al., 2008). Cuando se utilizaron modelos en tres dimensiones, éstos fueron representaciones muy simples y reduccionistas de las extremidades humanas (Gardano y Dabnichki, 2006). Gardano y Dabnickki (2006) utilizaron figuras geométricas tridimensionales estándar para representar el miembro superior, lo cual dio como resultado diferencias significativas entre el miembro humano y el modelo digital. Estas diferencias entre los modelos auténticos y computarizados podrían tener como consecuencia resultados numéricos menos precisos (Candalai y Reddy, 1992). De hecho, Candalai y Reddy (1992) llevaron a cabo una simulación del efecto de la geometría de la tuberosidad isquiática sobre el estrés de corte y compresión en los glúteos y demostraron que la influencia de la geometría en la magnitud del estrés podía ser significativa. Se halló una posible variación de más de 60% en el estrés de corte. A pesar de las diferencias entre los objetivos del trabajo de Candalai y Reddy (1992) y los estudios de natación, se debe reconocer la validez ecológica de la información que se ha obtenido, enfatizando la relevancia de los modelos explorados en lugar de la utilización de representaciones analíticas. Además, se debería tener en cuenta que la generación de una malla, primer escalón de las simulaciones numéricas, es un procedimiento difícil, en especial cuando se resuelven problemas en tres dimensiones. Por lo tanto, debería basarse en la información anatómica obtenida directamente (Aritan et al., 1997; Lecrivain et al., 2008; Marinho et al., 2008b; Marinho et al., 2009b).
Las imágenes obtenidas por resonancia magnética, las exploraciones por tomografía computada y láser parecen ser un buen método para diseñar auténticos modelos humanos (Aritan et al., 1997; Lecrivain et al., 2008; Marinho et al., 2008b; Marshall et al., 2004). El objetivo general de este método, también llamado proceso de ingeniería reversa, es construir un modelo virtual geométricamente idéntico a un objeto existente. La exploración y el manejo de la información son las dos partes principales en este proceso. En pocas palabras, se debe reunir la información necesaria de un objeto tridimensional y luego editar la información y traducirla en formatos más apropiados tales como los modelos de superficie (Lecrivain et al., 2008).
Al utilizar un modelo auténtico del cuerpo humano es posible mejorar la calidad de las técnicas de simulación numérica y proporcionar información útil a algunas cuestiones que permanecen poco claras en la técnica del nado. La posición relativa del pulgar durante el ciclo subacuático de la brazada es una de estas cuestiones. Se puede observar una gran variabilidad inter-sujeto en relación con las posiciones del pulgar que adoptan los nadadores de elite. Algunos nadadores mantienen el pulgar en aducción, otros mantienen el pulgar en abducción y otros lo mantienen en abducción parcial. De hecho, queda mucho por aprender sobre el efecto de la posición del pulgar y mientras tanto se han obtenido resultados similares a través de diferentes métodos de evaluación (Takagi et al., 2001). Schleihauf (1979) demostró que el pulgar en abducción parcial permite una mayor propulsión. Berger et al. (1997) hallaron que los modelos con diferentes abducciones/aducciones del pulgar mostraron muy pocas consecuencias en las fuerzas de arrastre pero sí tuvieron un efecto sobre las fuerzas de elevación. Takagi et al. (2001) informaron que la aducción y la abducción del pulgar tuvieron una influencia sobre la fuerza de elevación. El pulgar en abducción pareció ser una ventaja para generar la fuerza de elevación cuando el pulgar es el borde de ataque y el pulgar en aducción pareció ser una ventaja cuando es el meñique el que lidera el movimiento (Takagi et al., 2001). Para nuestro conocimiento, no existe ninguna investigación publicada que utilice un método numérico sobre la repercusión de la abducción / aducción del pulgar y con información antropométrica de la mano de los nadadores de elite.
Por lo tanto, el objetivo del presente estudio ha sido analizar las características hidrodinámicas de un modelo auténtico de la mano de un nadador con el pulgar en diferentes posiciones, utilizando técnicas de simulación numérica.
METODOS
Modelo Tridimensional
Exploración
Se llevaron a cabo exploraciones de sección cruzada de la mano derecha mediante la utilización de un escáner de tomografía computada Toshiba® Aquilion 4, utilizando una configuración V2.04 ER001. El sujeto fue un nadador masculino de nivel olímpico que participó en los Juegos Olímpicos del 2004 en Atenas. El sujeto permaneció recostado con el brazo derecho extendido hacia arriba, el antebrazo hacia abajo y el pulgar en tres posiciones: en abducción completa, en abducción parcial y en aducción (Figura 1). En la posición del pulgar en abducción completa el ángulo entre el índice y el pulgar fue de 68° y en la posición del pulgar en abducción parcial el ángulo entre estos dos dedos fue de 30°. La longitud de la mano, de la palma y el ancho de la mano del nadador era de 20.20 cm, 9.50 cm y 8.90 cm respectivamente. Este protocolo ha sido aprobado por el comité de ética pertinente de la institución en la que se realizó el estudio y el sujeto dio su consentimiento por escrito para participar en este trabajo.
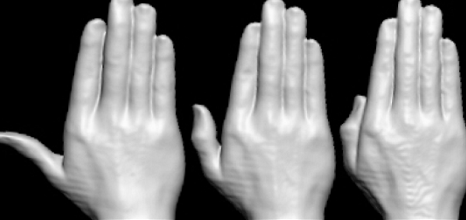
Figura 1. Modelos de la mano con el pulgar en diferentes posiciones: pulgar en abducción completa, en abducción parcial y en aducción.
Manipulación de los Datos
La transformación de los valores de las exploraciones por tomografía computada a coordenadas nodales en un sistema de coordenadas apropiado exige la utilización de técnicas de procesamiento de imágenes. El programa de procesamiento de imágenes utilizado en este estudio fue el Anatomics Pro®, que permitió obtener los límites de los segmentos humanos, creando una reconstrucción tridimensional de la mano del nadador.
En un primer lugar se prepararon los datos antes de llevar a cabo los procedimientos de procesamiento y conversión, es decir se observaron los datos obtenidos con la tomografía computada y se borraron las partes no relevantes del modelo anatómico. Este paso también se llevó a cabo utilizando el software FreeForm Sensable®. Por último, los datos se transformaron a formato IGES (*.igs), que pudieron leerse mediante el software Gambit/Fluent® para definir el método de elementos finitos a través de las superficies tridimensionales (Figure 2).

Figura 2. Modelo de la mano con el pulgar en abducción completa dentro del dominio (Ángulo de ataque = 0o, Ángulo de barrido hacia atrás = 0o).
Análisis Computacional de la Dinámica de Fluidos
La mayoría de los procedimientos para el análisis computacional de la dinámica de fluidos se dividen en tres etapas sucesivas: procesamiento previo, simulación y post-proceso. La etapa de procesamiento previo incluye la creación de un dominio computarizado donde se produzca la simulación de fluido, limitándolo a las condiciones externas y diferenciándolo en una cuadrícula de malla adecuada. La solución del problema de flujo está definida en los nodos dentro de cada celda. La certeza de una solución y su costo con respecto a la memoria necesaria para la computadora y el tiempo de cálculo dependen de la calidad de la cuadrícula. Las mallas óptimas a menudo no son uniformes: son más finas en las áreas de altos gradientes de presión y velocidad, y más bastas en las áreas con cambios relativamente pequeños. La simulación se realiza a través de un algoritmo iterativo hasta la convergencia. Luego las variables de interés (por ejemplo, las fuerzas hidrodinámicas) se extraen del campo del flujo computarizado (Lecrivain et al., 2008). Para obtener más detalles matemáticos puede referirse al apéndice.
Procesamiento Previo
Todo el dominio se colocó en una malla con 200.000 celdas. La cuadrícula era una malla híbrida compuesta de prismas y pirámides. Se utilizó un mallado adaptable para lograr un refinamiento óptimo de la malla. Por lo tanto, se realizaron esfuerzos significativos para asegurar que el modelo proporcionara resultados precisos, se disminuyó el nodo de separación de la cuadrícula en las áreas de altos gradientes de presión y velocidad.
Resolución del Flujo Estable
Se analizaron las simulaciones numéricas de un modelo tridimensional de la mano de un nadador según las condiciones de fluido fijo utilizando el código Fluent®. En el presente estudio se calcularon las fuerzas de fluido hidrodinámico producidas por la mano, de elevación (L) y de arrastre (D). Estas fuerzas son funciones de la velocidad del fluido, y se determinaron mediante la aplicación de las ecuaciones 1 y 2.
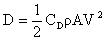 (1)
(1)
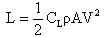 (2)
(2)
En las ecuaciones 1 y 2, V es la velocidad del agua, CD y CL son los coeficientes de arrastre y elevación, respectivamente, ρ es la densidad de fluido y A es el área de proyección del modelo para los diferentes ángulos de ataque utilizados en este estudio. Se define a la fuerza de arrastre como la fuerza que actúa paralela a la dirección del flujo y la fuerza de elevación yace perpendicular a la fuerza de arrastre.
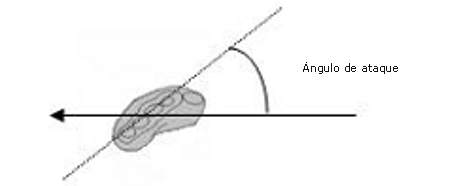
Figura 3. Ángulo de ataque (Schleihauf, 1979). La flecha representa la dirección del flujo.
El ángulo entre la mano y la dirección del flujo se define como ángulo de ataque (Figura 3) y el borde de ataque de la mano relativo al flujo es el ángulo de barrido hacia atrás (Figura 4). Para los cálculos se utilizaron ángulos de ataque de los modelos de mano de 0°, 45° y 90°, con un ángulo de barrido hacia atrás de 0° (el pulgar como borde de ataque) (Schleihauf, 1979). Las fuerzas medidas en los modelos de mano se analizaron en coeficientes de arrastre (CD) y de elevación (CL), utilizando las ecuaciones 1 y 2 y el coeficiente de arrastre resultante se calculó a través de la suma del CD y del CL, utilizando el teorema de Pitágoras.
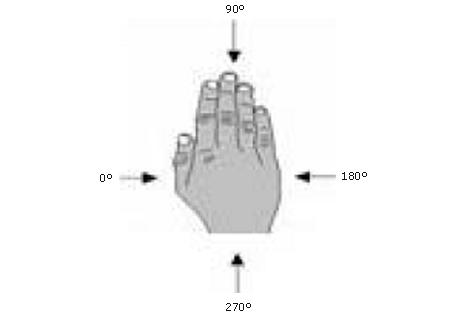
Figura 4. Ángulo de barrido hacia atrás (Schleihauf, 1979). La flecha representa la dirección del flujo.
Del lado izquierdo del acceso del dominio (Figura 2), el componente x de la velocidad se escogió de modo que estuviera dentro del rango de velocidades propias de la mano durante la trayectoria subacuática del nado en estilo crol: de 0.50 m-s-1 a 4.00 m-s-1, con incrementos de 0.50 m-s-1 (Lauder et al., 2001; Rouboa et al., 2006). Se supuso que los componentes de velocidad y y z eran igual a cero. Del lado derecho, la presión fue igual a 1 atm, pre-requisito fundamental para prevenir el reflejo del fujo. Alrededor del modelo, los tres componentes de la velocidad se consideraron iguales a cero para permitir la adhesión del fluido al modelo. Asimismo se consideró la acción de la fuerza de gravedad (g = 9.81 m-s-2), como también el porcentaje de turbulencia de 1% con 0.10 m de longitud (Bixler y Riewald, 2002; Marinho et al., 2008a). El fluido que se tuvo en cuenta fue agua, incompresible con la densidad (p = 996.6 x 10-9 kg-mm-3) y la viscosidad (|i= 8.571 x 10-7 kg/mm/s).
Las ecuaciones de Reynolds-Averaged Navier-Stokes incompresibles con el modelo k-épsilon estándar (k-ε) se tuvieron en cuenta y se implementaron en el código comercial Fluent®, como se mostró anteriormente (Moreira et al., 2006).
RESULTADOS
En las Figuras 5, 6 y 7 se presenta la evolución de los valores del CD y del CL de acuerdo a la velocidad del fluido y el ángulo de ataque para cada posición del pulgar. Para las tres posiciones del pulgar, el CD y el CL permanecieron casi constantes en todas las velocidades del fluido que se probaron (0.50-4.0 m-s-1). Sin embargo, fue posible notar una pequeña disminución en los coeficientes de fuerza, en especial de 0.50 a 1.50 m-s-1.
En las Figuras 8 y 9 se presentan los valores del CD y el CL que se obtuvieron para los diferentes ángulos de ataque y para las diferentes posiciones del pulgar para una velocidad del fluido de 2.0 m-s-1.
Es posible notar que los valores del CD se incrementaron con el ángulo de ataque. De hecho, el valor máximo del CD se produjo a un ángulo de ataque de 90°, presentando un valor de alrededor de 1.0 en los tres modelos.
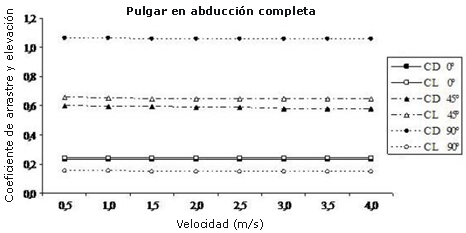
Figura 5. Coeficientes de arrastre y elevación vs velocidad del fluido para cada ángulo de ataque en la posición de pulgar en abducción completa.
Además, los valores del CD fueron casi similares en las tres posiciones diferentes del pulgar, aunque la posición con el pulgar en aducción presentó valores un poco más elevados en 0o, 45° y 90°.
El CL presentó los valores máximos en un ángulo de ataque de 45° (CL ≈ 0.6). Los valores del CL en los ángulos de ataque de 0o y 90° parecieron ser idénticos (CL ≈ 0.15). Además, la posición con el pulgar en abducción completa y con el pulgar en abducción parcial presentaron valores de CL más elevados cuando se la comparó con la posición del pulgar en aducción en ángulos de ataque de 0o y 45°. Sin embargo, la posición con el pulgar en abducción completa presentó valores más elevados cuando se la comparó con la posición del pulgar en abducción parcial en 0o y 45°. En un ángulo de ataque de 90° los valores del CL fueron idénticos sin tomar en consideración la posición del pulgar.
Al analizar el coeficiente de fuerza resultante (Figura 10), se puede notar que la posición del pulgar en abducción presentó valores más elevados que las posiciones con el pulgar en abducción parcial y en aducción en ángulos de ataque de 0° y 45°. No obstante, en un ángulo de ataque de 90° la posición del pulgar en aducción presentó el valor más elevado de coeficiente de fuerza resultante.
DISCUSION
El objetivo del presente estudio ha sido analizar las características hidrodinámicas de un modelo auténtico de la mano de un nadador con el pulgar en diferentes posiciones utilizando técnicas de simulación numérica.
En esta investigación se ha intentado mejorar los estudios previos que aplicaron las técnicas numéricas al análisis de la propulsión del nado, utilizando un modelo más realista de la mano de un nadador. De hecho, las exploraciones por tomografía computada permitieron la creación de un auténtico modelo anatómico digital de la mano de un nadador (Aritan et al., 1997).
Uno de los beneficios más importantes de los procedimientos de simulación numérica es que le permite al usuario modificar las entradas en el modelo para determinar cómo afectan sus cambios a las condiciones de flujo resultantes. Con respecto a la natación, los cambios en la técnica se pueden examinar utilizando el modelo, en lugar del método de “ensayo y error” que se utiliza normalmente.
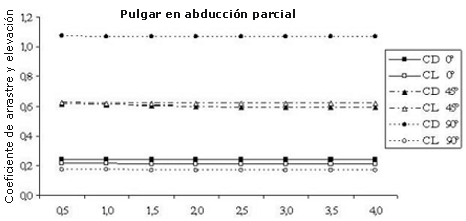
Figura 6. Coeficientes de arrastre y elevación vs velocidad del fluido para cada ángulo de ataque en la posición de pulgar en abducción parcial.
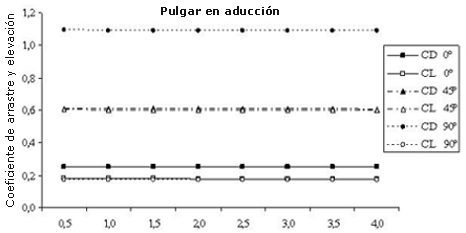
Figura 7. Coeficientes de arrastre y elevación vs velocidad del fluido para cada ángulo de ataque en la posición de pulgar en aducción.
En el presente trabajo se han analizado las fuerzas hidrodinámicas producidas por la mano del nadador con el pulgar en diferentes posiciones como lo utilizan los nadadores de alto nivel.
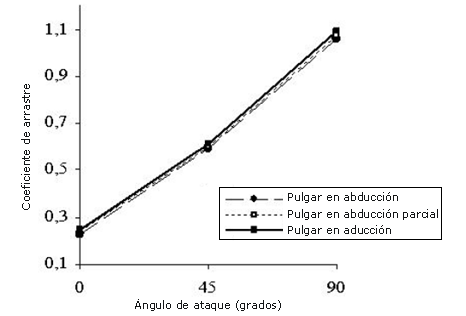
Figura 8. Valores del coeficiente de arrastre que se obtuvieron para los diferentes ángulos de ataque y para las diferentes posiciones del pulgar. Ángulo de extensión hacia atrás = 0° y velocidad del fluido = 2.0 m-s-1.
Para las tres posiciones del pulgar, los valores de CD y el CL permanecieron casi constantes en todas las velocidades del fluido que se probaron. Ya se ha reportado de una observación similar en otros estudios numéricos (Alves et al., 2007; Bixler y Riewald, 2002; Rouboa et al., 2006; Silva et al., 2005). Sin embargo, en el presente estudio, se observó una pequeña disminución en los CD y CL, en especial de 0.50 a 1.50 m-s-1. Berger et al. (1995) y Bixler y Riewald (2002) observaron una tendencia similar para las velocidades más bajas, en un experimento llevado a cabo en un canal de ensayos (towing tank) y utilizando técnicas numéricas, respectivamente. En las velocidades más bajas, al incrementar la velocidad se produjo una disminución muy pequeña de los valores de los coeficientes de fuerza. No obstante, desde un punto de vista práctico, los coeficientes se consideraron constantes puesto que las fuerzas a estas velocidades son relativamente bajas (Bixler y Riewald, 2002).
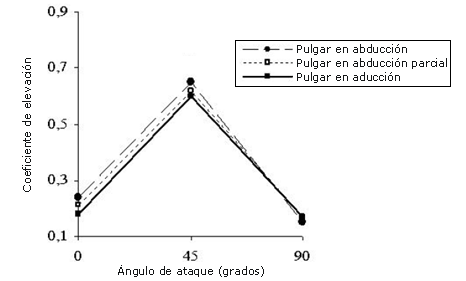
Figura 9. Valores del coeficiente de elevación que se obtuvieron para los diferentes ángulos de ataque y para las diferentes posiciones del pulgar. Ángulo de extensión hacia atrás = 0° y velocidad del fluido = 2.0 m-s-1.
Los valores del CD que produjo la mano del nadador fueron muy similares en relación con las tres posiciones del pulgar. Sin embargo, la posición del pulgar en aducción presentó valores apenas más elevados en los ángulos de ataque que se probaron en el presente estudio. Además, los valores del CL cambiaron con la posición del pulgar en ángulos de ataque de 0° y 45°, aunque en un ángulo de ataque de 90° los valores de las diferentes posiciones del pulgar fueron idénticos. En 0° y 45°, la posición con el pulgar en abducción completa presentó los valores más elevados de CL.
Schleihauf (1979) estudió los cambios en los valores del CL como una función de la posición del pulgar (pulgar en abducción de 100%, en abducción de 75% y en abducción de 50%). No obstante los autores no estudiaron el CD ni la posición del pulgar en aducción. En el estudio de Schleihauf (1979), la posición con el pulgar en abducción completa mostró un máximo del CL en un ángulo agudo de ataque de 15°, mientras que los modelos con el pulgar en abducción parcial mostraron un valor máximo del CL en ángulos de ataque mayores (45°-60°). En estos ángulos de ataque la posición con el pulgar en abducción parcial presentó valores más elevados cuando se la comparó con la del pulgar en abducción completa. Berger et al. (1997) informaron que la posición del pulgar determinó las fuerzas de elevación, aunque las fuerzas de arrastre fueron influenciadas por la abducción/aducción del pulgar. Además, Takagi et al. (2001) calcularon las fuerzas de arrastre y elevación de las mediciones directas de las diferencias de presión entre el dorso y la palma de la mano en un modelo de resina con el pulgar en abducción y aducción. Los resultados experimentales revelaron que la posición del pulgar influenció la fuerza del fluido en toda la mano, en especial en la fuerza de elevación. Para un ángulo de barrido hacia atrás de 0° (como se utilizó en el presente estudio), el modelo con el pulgar en abducción pareció ser ventajoso para generar la fuerza de elevación, mientras que para un ángulo de barrido hacia atrás de 180° (el meñique como borde de ataque), pareció preferible el pulgar en aducción. Sin embargo, en el estudio de Takagi et al. (2001), el CD presentó valores similares en las dos posiciones del pulgar para un ángulo de movimiento hacia atrás de 0°. Para un ángulo de movimiento hacia atrás de 180°, la posición del pulgar en aducción presentó valores más elevados.
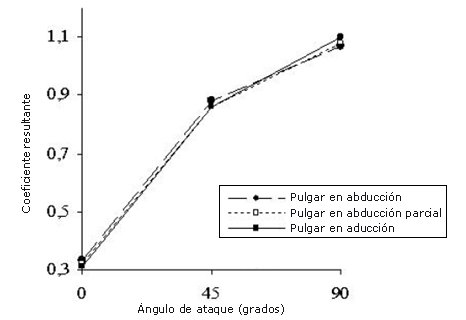
Figura 10. Valores del coeficiente de fuerza resultante que se obtuvieron para los diferentes ángulos de ataque y para las diferentes posiciones del pulgar. Ángulo de extensión hacia atrás = 0° y velocidad del fluido = 2.0 m-s-1.
A pesar de algunas diferencias en los resultados de distintos estudios, parece ser que cuando el pulgar lidera el movimiento (ángulo de barrido hacia atrás de 0°) sería preferible una posición de mano con el pulgar en abducción en el plano de la mano a una posición con el pulgar en aducción. En este caso, es posible que se sugiera que durante la fase de barrido abajo-afuera de la trayectoria subacuática en las técnicas de mariposa, pecho y crol, y en la fase de salida de la técnica de espalda la posición con el pulgar en abducción podría resultar beneficiosa para los nadadores. Por otro lado, en base al estudio de Takagi et al. (2001) solamente, cuando el meñique lidera el movimiento (ángulo de barrido hacia atrás de 180°), durante la fase de salida en mariposa y pecho, y en algunas partes de la fase de barrido hacia abajo en espalda y de subida en crol, parecería que es preferible la posición con el pulgar en aducción. Una posible explicación puede estar relacionada con el cambio en el flujo alrededor de la mano debido a la posición del pulgar: la fuerza de elevación mejora debido a un incremento de la presión sobre la palma de la mano y una disminución de la presión sobre el dorso de la misma (Colwin, 1992; Takagi et al., 2001).
En el presente estudio sólo se ha analizado el ángulo de barrido hacia atrás de 0°. Por lo tanto estas consecuencias técnicas deben tomarse con seriedad. De hecho, se garantizan más estudios que analicen la posición del pulgar con diferentes ángulos de barrido hacia atrás y una mayor variedad de ángulos de ataque. Además, se debe tener cuidado al generalizar estos resultados puesto que cada nadador tiene una forma diferente de la mano y los principales hallazgos podrían variar entre los diferentes sujetos. No obstante, al parecer, la posición del pulgar puede jugar un papel importante en la optimización de la técnica de nado. Al analizar el coeficiente de fuerza resultante, se descubrió que la posición del pulgar en abducción presentó valores más elevados que las posiciones con el pulgar en abducción parcial y en aducción en ángulos de ataque de 0° y 45°. Con un ángulo de ataque de 90° la posición del pulgar en aducción presentó el valor más elevado de coeficiente de fuerza resultante. Esta información parece corroborar los hallazgos previos ya mencionados. Para las posiciones de mano en las que la fuerza de elevación puede ser importante (Figuras 5, 6 y 7), la abducción del pulgar puede resultar beneficiosa para los nadadores. Además, con ángulos de ataque mayores, en los que la fuerza de arrastre es la dominante, puede ser preferible la aducción del pulgar. La información sobre el coeficiente de fuerza resultante mostró que los mayores valores se produjeron cuando el ángulo de ataque fue de 90°. Sanders (1997) observó que las mayores fuerzas resultantes se produjeron cuando la mano tuvo un ataque de alrededor de 90°, sin tener en cuenta el ángulo de barrido hacia atrás. Estos resultados son interesantes en vista de que los nadadores utilizan movimientos de remo en lugar de tirar la mano directamente en oposición a la dirección de movimiento deseada con ángulos de ataque cercanos a los 90° para mejorar la eficacia del movimiento (Sanders, 1999). Por otro lado, continúa el interrogante sobre si esta fuerza resultante se puede utilizar para propulsarse en la dirección deseada. Por lo tanto, en el futuro parece importante analizar la fuerza de propulsión efectiva que produce la mano del nadador en la trayectoria subacuática.
En todas las posiciones del pulgar el CD obtuvo el valor más elevado en un ángulo de ataque de 90°, es decir, donde el plano de la mano fue directamente perpendicular a la dirección del flujo. Otros que utilizaron métodos experimentales (Berger et al., 1995; Sanders, 1999) y numéricos (Alves et al., 2007; Rouboa et al., 2006) reportaron el mismo resultado, indicando la contribución del área de superficie de la mano al incremento del CD.
El CL pareció tener una influencia residual en la fuerza de propulsión que generó la mano para ángulos de ataque de 0° y 90°, pero es importante en un ángulo de ataque de 45°. Estos hallazgos son similares a aquellos que se encontraron en estudios experimentales (Berger et al., 1995; Sanders, 1999; Schleihauf, 1979; Wood, 1977) y numéricos (Alves et al., 2007; Bixler y Riewald, 2002), que informan sobre el importante papel de la fuerza de elevación para la producción de la fuerza de propulsión general de la mano en las fases subacuáticas de las brazadas cuando el ángulo de ataque es cercano a los 45° (por ejemplo, en la fase de barrido abajo-afuera). De hecho, aunque el CD y el CL fueron muy similares en las tres posiciones del pulgar en ángulos de ataque de 0° y 45°, fue posible observar que para las posiciones con el pulgar en abducción completa y en abducción parcial el CL presentó valores mayores que el CD en un ángulo de ataque de 45°. Por lo tanto, parece esencial reforzar la necesidad de analizar un rango mayor de ángulos de ataque y ángulos de movimiento hacia atrás, intentando aclarar la verdadera importancia de la fuerza de elevación para la producción de la fuerza de propulsión. La fuerza de elevación cumple un papel importante en otros ángulos de ataque más que en el de 45°, como informó Schleihauf (1979) en un ángulo de 15° y Sanders (1999) en ángulos de movimiento hacia atrás en lugar de 0°.
En el presente estudio, a pesar del hecho de que sólo se hicieron modelos de los coeficientes de arrastre y elevación bajo condiciones de fluido estable, se tiene en cuenta que el método numérico que se llevó a cabo es altamente satisfactorio. En primer lugar, la utilización de un modelo auténtico tridimensional de la mano de un nadador pareció ser un paso importante para la convergencia entre la información experimental y la computarizada. En segundo lugar, fue posible variar la posición del pulgar e investigar el efecto en el CD y el CL producidos por la mano del nadador. Sin embargo, esta línea de investigación debe mejorarse teniendo en cuenta los efectos inestables del movimiento, tales como las aceleraciones, desaceleraciones y rotación de los segmentos de propulsión. De hecho, Sanders (1999), Bergeret al. (1999) y Rouboa et al. (2006) demostraron que los movimientos estables e inestables pueden llevar a resultados diferentes, llegando a la conclusión de que los efectos inestables deberían tenerse en cuenta a la hora de buscar estimaciones precisas de las fuerzas del nado. Por consiguiente, el efecto de la posición del pulgar en las características hidrodinámicas de la mano de un nadador se debe continuar investigando mediante análisis numéricos que dependan del tiempo con funciones definidas por el usuario y mallas móviles.
CONCLUSION
La posición con el pulgar en aducción presentó valores del coeficiente de arrastre apenas más elevados en comparación con la del pulgar en abducción (aunque los valores fueron muy similares). Además, la posición con el pulgar en abducción completa permitió incrementar el coeficiente de elevación de la mano en ángulos de ataque de 0° y 45°. En un ángulo de ataque de 90° los valores del coeficiente de elevación fueron idénticos, sin tomar en consideración la posición del pulgar.
La combinación de los coeficientes de arrastre y fuerza resultante (coeficiente de fuerza resultante), mostró que la posición del pulgar en abducción completa presentó valores más elevados que las posiciones con el pulgar en abducción parcial y en aducción en ángulos de ataque de 0° y 45°. No obstante, en un ángulo de ataque de 90° la posición del pulgar en aducción presentó el valor más elevado del coeficiente de fuerza resultante. Estos resultados sugirieron que, para las posiciones de mano en las que la fuerza de elevación puede resultar importante, la abducción del pulgar puede ser beneficiosa, mientras que en ángulos de ataque más elevados, en los que la fuerza de arrastre es la dominante, para los nadadores puede resultar preferible la aducción del pulgar.
Puntos Clave
- Las técnicas de simulación numérica pueden brindar respuestas a problemas que hubieran sido imposibles de obtener mediante la utilización de métodos experimentales.
- Las exploraciones por tomografía computada permitieron la creación de un auténtico modelo anatómico digital de la mano de un nadador.
- La posición con el pulgar en aducción presentó valores apenas más elevados del coeficiente de arrastre que las posiciones con el pulgar en abducción.
- La posición con el pulgar en abducción completa permitió incrementar el coeficiente de elevación de la mano en ángulos de ataque de 0 y 45 grados.
- Para las posiciones de mano en las que la fuerza de elevación puede resultar importante, puede ser mejor la abducción del pulgar, mientras que en ángulos de ataque más elevados, en los que la fuerza de arrastre es la dominante, para los nadadores puede resultar preferible la aducción del pulgar.
AGRADECIMIENTOS
El presente trabajo ha sido financiado por el gobierno portugués por medio de las Subvenciones de la Fundación de Ciencia y Tecnología (SFRH/BD/25241/2005; POCTI/DES/58872/2004).
Se agradece al personal del Departamento de Radiología del Hospital de Sao Joao, en Porto, Portugal, y personalmente a la directora del departamento, la Profesora Isabel Ramos por las importantes contribuciones. Asimismo se expresa gratitud a Med Mat Innovation Company, en Maia, Portugal, en especial al Profesor José Domingos Santos y al ingeniero Bruno Sá por sus contribuciones.
APENDICE
La metodología de las técnicas de simulación numérica consiste en un modelo matemático aplicado al flujo de fluidos en un determinado dominio que reemplaza las complejas ecuaciones de flujo de fluidos de Navier-Stokes con expresiones algebraicas discretizadas. Estas ecuaciones pueden resolverse mediante cálculos iterativos. Se utilizó el código Fluent® para desarrollar y resolver estas ecuaciones utilizando el método de volumen finito, donde las ecuaciones están integradas en cada volumen de control. Por consiguiente, la ecuación de continuidad, las ecuaciones de conservación de impulso y las ecuaciones de conservación de energía turbulenta y disipada (k-s) (para un flujo incompresible en ejes cartesianos) se escribieron de manera conservadora como:
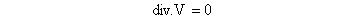 (3)
(3)
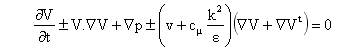 (4)
(4)
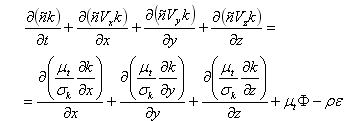 (5)
(5)
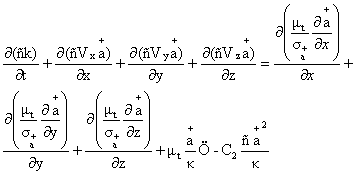 (6)
(6)
Donde k es la energía cinética turbulenta y ε es el índice de disipación de la energía cinética turbulenta. Vx, Vy y Vz representan los componentes de la x, y y z de V. μt es la viscosidad turbulenta y ρ representa la densidad del flujo. υ es la viscosidad cinemática, Φ es la tensión de la presión, C2, Cμ, σε y σk son las constantes del modelo, 1.92, 0.09, 1.30 y 1.00, respectivamente (Silva et al., 2008).
Referencias
1. Alves, F., Marinho, D., Leal, L., Rouboa, A. and Silva, A (2007). 3-D computational fluid dynamics of the hand and forearm in swimming. Medicine and Science in Sports and Exercise 39(Suppl. 1), S9
2. Aritan, S., Dabnichki, P. and Bartlett, R (1997). Program for generation of three-dimensional finite element mesh form magnetic resonance imaging scans of human limbs. Medical Engineering and Physics 19(8), 681-689
3. Berger, M.A., de Groot, G. and Hollander, A.P (1995). Hydrodynamic drag and lift forces on human hand arm models. Journal of Biomechanics 28(2), 125-133
4. Berger, M.A., de Groot, G. and Hollander, A.P (1997). of hand shape on force generation during swimming. In: Proceedings of the XII FINA World Congress on Sports Medicine. Eds: Eriksson, B.O. and Gullstrand, L. Goteborg: Chalmers Reproservice. 389-396
5. Berger, M.A., Hollander, A.P. and de Groot, G (1999). Determining propulsive force in front crawl swimming: a comparison of two methods. Journal of Sports Sciences 117, 97-105
6. Bixler, B.S. and Riewald, S (2002). Analysis of swimmers hand and arm in steady flow conditions using computational fluid dynamics. Journal of Biomechanics 35, 713-717
7. Bixler, B.S. and Schloder, M (1996). Computational fluid dynamics: an analytical tool for the 21st century swimming scientist. Journal of Swimming Research 11, 4-22
8. Boulding, N., Yim, S.S., Keshavarz-Moore, E., Ayazi Shamlou, P. and Berry, M (2002). Ultra scaledown to predict filtering centrifugation of secreted antibody fragments from fungal broth. Biotechnology and Bioengineering 79(4), 381-388
9. Candalai, R.S. and Reddy, N.P (1992). Stress distribution in a physical buttock model: effect of simulated bone geometry. Journal of Biomechanics 15, 493-504
10. Colwin, C.M (1992). Swimming into the 21st century. Leisure Press, Illinois
11. Dabnichki, P. and Avital, E (2006). Influence of the position of crew members on aerodynamics performance of two-man bobsleigh. Journal of Biomechanics 39(15), 2733-2742
12. Gardano, P. and Dabnichki, P (2006). On hydrodynamics of drag and lift of the human arm. Journal of Biomechanics 39, 2767-2773
13. Guerra, D., Ricciardi, L., Laborde, J.C. and Domenech, S (2007). Predicting gaseous pollutant dispersion around a workplace. Journal of Occupational and Environmental Hygiene 4(8), 619-633
14. Kellar, W.P., Pearse, S.R.G. and Savill, A.M (1999). Formula 1 car wheel aerodynamics. Sports Engineering 2(4), 203-212
15. Lauder, M., Dabnichki, P. and Bartlett, R (2001). Improved accuracy and reliability of sweepback angle, pitch angle and hand velocity calculations in swimming. Journal of Biomechanics 34, 31-39
16. Lecrivain, G., Slaouti, A., Payton, C. and Kennedy, I (2008). Using reverse engineering and computational fluid dynamics to investigate a lower arm amputee swimmers performance. Journal of Biomechanics 41, 2855-2859
17. Marinho, D.A., Reis, V.M., Alves, F.B., Vilas-Boas, J.P., Machado, L., Silva, A.J. and Rouboa, A.I (2008). The hydrodynamic drag during gliding in swimming. Journal of Applied Biomechanics, in press
18. Marinho, D.A., Reis, V.M., Vilas-Boas, J.P., Alves, F.B., Machado, L., Rouboa, A.I. and Silva, A.J (2008). Design of a three-dimensional hand/forearm model to apply Computational Fluid Dynamics. Brazilian Archives of Biology and Technology, in press
19. Marinho, D.A., Rouboa, A.I. and Silva, A.J (2009). The study of swimmers hand and forearm using Computational Fluid Dynamics. Science et Sports, in press
20. Marinho, D.A., Barbosa, T.M., Reis, V.M., Kjendlie, P.L., Alves, F.B., Vilas-Boas, J.P., Machado, L., Silva, A.J and Rouboa, A.I (2009). Swimming propulsion forces are enhanced by a small finger spread. Journal of Applied Biomechanics, in press
21. Marshall, I., Zhao, S., Papathanasopoulou, P., Hoskins, P. and Xui, Y (2004). MRI and CFD studies of pulsatile flow in healthy and stenosed carotid bifurcation models. Journal of Biomechanics 37, 679-687
22. Moreira, A., Rouboa, A., Silva, A.J., Sousa, L., Marinho, D., Alves, F., Reis, V., Vilas-Boas, J.P., Carneiro, A. and Machado, L (2006). Computational analysis of the turbulent flow around a cylinder. Portuguese Journal of Sport Sciences 6(Suppl. 1), 105
23. Pallis, J.M., Banks, D.W. and Okamoto, K.K (2000). 3D computational fluid dynamics in competitive sail, yatch and windsurfer design. In: The Engineering of Sport: Research, Development and Innovation. Eds: Subic, F. and Haake, M. Oxford: Blackwell Science. 75-79
24. Rouboa, A, Silva, A., Leal, L., Rocha, J. and Alves, F. (2006). The effect of swimmers hand/forearm acceleration on propulsive forces generation using Computational Fluid Dynamics. Journal of Biomechanics 39(7), 1239-1248
25. Sanders, R.H (1997). Hydrodynamic characteristics of a swimmer hand with adducted thumb: implications for technique. In: Proceedings of the XII FINA World Congress on Sports Medicine. Eds: Eriksson, B.O. and Gullstrand, L. Goteborg: Chalmers Reproservice. 429-434
26. Sanders, R.H (1999). Hydrodynamic characteristics of a swimmers hand. Journal of Applied Biomechanics 15, 3-26
27. Schleihauf, R.E (1979). A hydrodynamic analysis of swimming propulsion. In: Swimming III. Eds: Terauds, J. and Bedingfield, E.W. Baltimore: University Park Press. 70-109
28. Silva, A., Rouboa, A., Leal, L., Rocha, J., Alves, F., Moreira, A., Reis, V. and Vilas-Boas, J.P (2005). Measurement of swimmers hand/forearm propulsive forces generation using computational fluid dynamics. Portuguese Journal of Sport Sciences 5(3), 288-297. (In Portuguese: English abstract)
29. Silva, A.J., Rouboa, A., Moreira, A., Reis, V.M., Alves, F., Vilas-Boas, J.P. and Marinho, D.A (2008). Analysis of drafting effects in swimming using computational fluid dynamics. Journal of Sports Science and Medicine 77(1), 60-66
30. Takagi, H., Shimizu, Y., Kurashima, A. and Sanders, R (2001). Effect of thumb abduction and adduction on hydrodynamic characteristics of a model of the human hand. In: Proceedings of Swim Sessions of the XIX International Symposium on Biomechanics in Sports. Eds: Blackwell, J. and Sanders, R. San Francisco: University of San Francisco. 122-126
31. Wood, T.C (1977). A fluid dynamic analysis of the propulsive potential of the hand and forearm in swimming. Master of Science Thesis, Dalhouise University Press, Halifax, NS
32. Zaidi, H., Taiar, R., Fohanno, S. and Polidori, G (2008). Analysis of the effect of swimmers head position on swimming performance using computational fluid dynamics. Journal of Biomechanics 41, 1350-1358