Estadística aplicada al Fútbol. Parte II.

Organización de los datos. Parte II.

En la Parte I del Blog anterior, mencionábamos que ordenar los datos en una columna de mayor a menor por ejemplo, era una forma sencilla de organizar los valores cuando el número de datos del que disponíamos era pequeño (aproximadamente 20 o menos).

Pero imaginemos que queremos procesar un mayor número de datos, por ejemplo 100 determinaciones, como podría pasar si evaluáramos a las divisiones inferiores de un club. En este caso ya no es tan cómodo tener una visión en una sola hoja del comportamiento de los datos. Claro que podemos hacerlo, pero tendremos 100 filas con los datos individuales de cada medición que abarcarán bastante espacio. En estos casos, además de la confección de un listado, podemos organizar los datos a través de una Tabla de Distribución de Frecuencias.

El número de veces que un valor de la medida se repite en nuestra lista de datos se denomina como “frecuencia absoluta” (fa). Además de la fa, también podemos tener listada la “frecuencia relativa” de los datos (fr). En este caso, obtenemos información acerca de la “proporción” con la que los datos se presentan. Para obtener la fr no tenemos mas que dividir la fa de cada dato por el total (n) de observaciones que disponemos: (fr: fa/n). El resultado de esa proporción nos informará un valor entre 0-1, y multiplicando por 100 el resultado anterior, obtendremos el dato de la frecuencia relativa porcentual del los datos (fr%), que entonces nos informará un resultado en un intervalo de 0-100%. En futuros Blog, veremos la importancia que tiene la frecuencia relativa para obtener los percentiles, un cálculo de gran utilidad especialmente en el área de las ciencias biológicas.

En general, los datos que procesamos de las evaluaciones de los planteles de fútbol se encuentran en unidades de medida de tiempo, distancias, etc. con lo que es poco probable que tengamos dentro de un plantel un grupo que haya recorrido “exactamente” la misma cantidad de metros durante un test, sumado a la heterogeneidad de valores que podemos encontrar debido a las diferentes posiciones de cada jugador en la cancha. Es decir, que el numero de veces que se repite un dato es baja (o sea, baja fa). Esto significaría que nuestra tabla de organización de datos no se acotaría demasiado si listáramos la frecuencia de los datos, debido a la variabilidad de los valores que tenemos.

Qué podemos hacer en estos casos para tener los datos en una sola tabla donde podamos visualizar de manera global y compacta los valores obtenidos?

Una buena herramienta seria elaborar la misma Tabla de Distribución de Frecuencias que mencionamos anteriormente pero la organizamos por Intervalos. Es decir, organizaremos nuestros datos en una tabla, pero agruparemos por intervalos las distancias recorridas y le calcularemos su frecuencia de aparición de manera absoluta y relativa entre el total de las determinaciones.

Por ejemplo, aquí se presentan datos de la distancia recorrida en el test de Yo-Yo de recuperación intermitente nivel 1 en 35 jugadores de fútbol (datos ya ordenados de menor a mayor):

1240 1320 1480 1560 1600 1600 1640

1760 1840 1880 1880 1920 1920 1960

2000 2160 2160 2360 2360 2400 2560

2560 2600 2680 2800 2800 2840 2880

2920 2920 3000 3080 3160 3160 3240

No hay una regla específica para la construcción de los intervalos, todo dependerá del detalle que queramos dar a los datos, pero debemos asegurarnos que todos los valores que medimos queden incluidos en un intervalo. En general, el numero de intervalos suele variar entre 5-15 (Di Rienzo y cols 2008) o entre 10-20 (Vincent 2005). Si hacemos pocos intervalos, el numero de datos que tendremos en cada intervalo será muy grande, es decir que habrá una gran concentración de datos y eso podría llegar a sesgar nuestra idea de lo que realmente ocurre con la distribución de los datos. Si realizamos una gran cantidad de intervalos, probablemente la información se diluya y se divida demasiado y la tabla nuevamente vuelva a ser muy larga, con pocos o ningún dato en algunos intervalos.

Veamos un ejemplo de la tabla de distribución de frecuencias para esos 35 datos, agrupada en 10 intervalos:

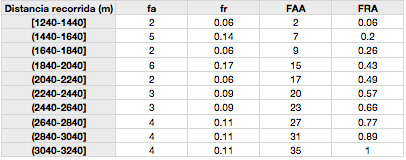
Tabla de distribución de frecuencias agrupada en 10 intervalos para la distancia recorrida durante el test YoYo de recuperación intermitente nivel 1 en 35 jugadores de fútbol. fa: frecuencia absoluta, fr: frecuencia relativa, FAA: frecuencia absoluta acumulada, FRA: frecuencia relativa acumulada.

En la columna de la fa registramos el numero de jugadores que recorrieron distancias en el test dentro de cada intervalo, mientras que en la columna de fr registramos la proporción de jugadores que recorrieron distancias en cada intervalo. Por ejemplo, si observamos la primera fila de las fa y fr podemos decir que 2 jugadores de 35 recorrieron una distancia entre 1240-1440 m en el test de Yo-Yo de recuperación intermitente nivel 1, lo que representa de manera relativa porcentual un 6% (0.06 *100). Pero también podemos ver que otro 6% completó distancias entre 1640-1840 m y entre 2040-2240 m.

Si observamos la primera columna de los intervalos, encontramos que el valor de los extremos de la derecha es el mismo que el valor del extremo de la izquierda del intervalo. Que ocurre si un jugador recorrió por ejemplo 1440 m, en que intervalo lo ubicamos? En este caso la representación con un corchete significa que ese valor esta incluido en ese intervalo (intervalo cerrado), mientras que si usamos los paréntesis, implica que el valor no esta incluido (intervalo abierto). Uno puede elaborar el intervalo como lo desee, abierto por izquierda y cerrado por derecha o viceversa, pero tiene que definirlo previamente para asegurar que los datos sean ubicados en el intervalo correcto.

En los siguientes gráficos se representan los resultados de la fa y fr que obtuvimos en la tabla de distribución de frecuencias agrupadas por intervalos.

Es importante aclarar que si bien la variable que estamos analizando (distancia recorrida) es una variable numérica continua y su representación grafica debería realizarse a través de un histograma (veremos en futuros blogs este concepto), las variables continuas pueden ser tratadas como discretas cuando se las trabaja mediante intervalos (Di Rienzo y cols 2008) y así graficarlas mediante un gráfico de barras como se ha hecho en este blog:

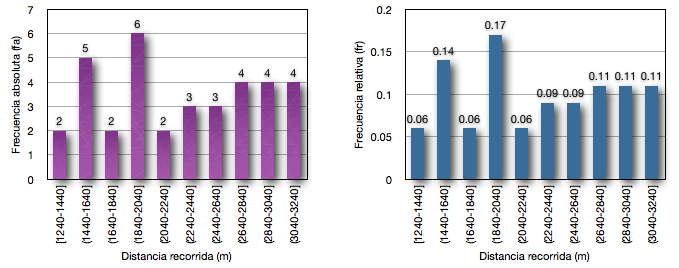
Gráfico 1. A (Izquierda) Distribución de la frecuencia absoluta, y B (Derecha) distribución de la frecuencia relativa en 35 jugadores de fútbol de la distancia recorrida durante el test YoYo de recuperación intermitente nivel 1.

Si observamos las ultimas dos columnas de la tabla, tenemos listados dos nuevos cálculos: la Frecuencia Absoluta Acumulada (FAA) y la Frecuencia Relativa Acumulada (FRA). Las frecuencias acumuladas, nos revelan de manera rápida cuantos jugadores recorrieron una distancia igual o menor que un determinado intervalo de distancia, y del mismo modo que en el caso anterior podemos decir lo mismo pero de manera relativa (FRA) y relativa porcentual.

Para calcular las frecuencias acumuladas, simplemente tenemos que ir sumando en la columna el valor de la fila precedente, tanto de la fila de la columna de la fa como de alguna de las fr (fr o fr%), de allí su nombre de “acumulada”.

Gráficamente podemos observar los valores acumulados:

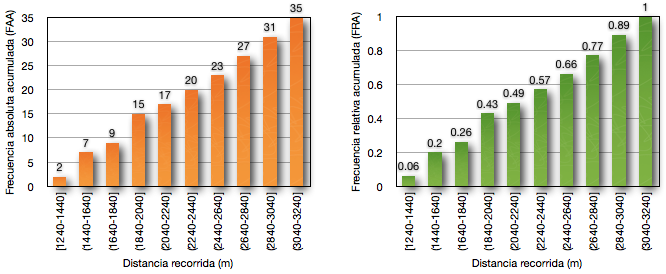
Gráfico 2. A (Izquierda) Distribución de la frecuencia absoluta acumulada, y B (Derecha) distribución de la frecuencia relativa acumulada en 35 jugadores de fútbol de la distancia recorrida durante el test YoYo de recuperación intermitente nivel 1.

De estos gráficos podemos ver de manera absoluta por ejemplo, que 20 jugadores de 35 recorrieron distancias entre 2240 – 2440 m o menos, o que 9 jugadores de 35 recorrieron distancias entre 1640 – 1840 o menos. Del mismo modo, visto de manera relativa acumulada, el 57% de los jugadores recorrieron distancias entre 2240 – 2440 m o menos, o que el 26% de los jugadores recorrieron distancias entre 1640 – 1840 m o menos.

En los gráficos que siguen (gráficos 3 y 4), simplemente les dejo la misma información pero agrupada por medio de diferentes intervalos. En el primer caso (gráfico 3) he agrupado los 35 jugadores en 5 intervalos, mientras que en el segundo caso (gráfico 4) en 16 intervalos, para que observen como los mismos datos pueden analizarse de manera diferente en cada caso. Mientras menos intervalos tenemos mayores fa en cada intervalo, mientras que si el numero de intervalos se hace mayor, claramente pude verse que el numero de casos en cada intervalo de distancia recorrida se hace mas pequeño.

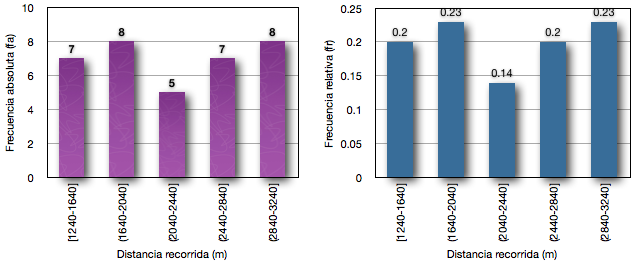
Gráfico 3. A (izquierda) Distribución de la frecuencia absoluta, y B (Derecha) distribución de la frecuencia relativa en 35 jugadores de fútbol de la distancia recorrida durante el test YoYo de recuperación intermitente nivel 1. Datos agrupados en 5 intervalos.

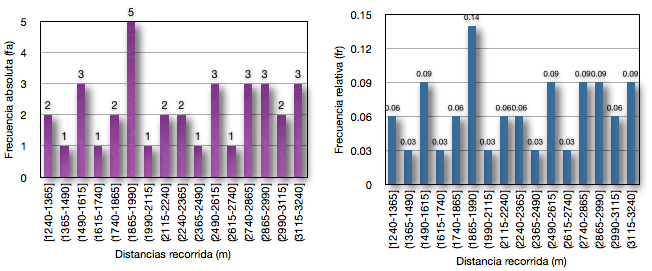
Gráfico 4. A (izquierda) Distribución de la frecuencia absoluta, y B (derecha) distribución de la frecuencia relativa en 35 jugadores de fútbol de la distancia recorrida durante el test YoYo de recuperación intermitente nivel 1. Datos agrupados en 16 intervalos.

Esta forma de organizar los datos a través del uso de tablas de distribución de frecuencias por intervalos es particularmente importante cuando el numero de datos es grande, ya que podemos agruparlos y analizar su comportamiento de una manera globalmente representada ya sea en una tabla o en un gráfico. Si bien esta herramienta es muy útil comparativamente con la lista individual de datos, tiene la desventaja que al tener los datos agrupados, perdemos información de los datos individuales de cada medición en esa representación.

Referencias

Di Rienzo JA, Casanoves F, Gonzalez LA, Tablada EM, Díaz MP, Robledo CW, Balzarini MG (2008). Estadística para las Ciencias Agropecuarias. 7 Edición, primera impresión. Editorial Brujas.

Vincent WJ (2005). Statistics in kinesiology. 3rd Edition. Human Kinetics.