Estadística Aplicada al Fútbol. Medidas de Posición. Parte I. Uso de la Media.

Uso de la Media para Datos No Agrupados

En los blogs anteriores hemos analizado como podemos organizar un reducido y un elevado numero de datos.

Ahora bien, una vez que los datos están listados, también podemos verlos y analizarlos de una manera aun mas condensada que en una tabla. Esta manera mas resumida es a través de los que se conoce en estadística como medidas de posición, localización o de tendencia central. Como ejemplo de estas medidas mas utilizadas hallamos a la media muestral, la mediana muestral, los cuantiles, y la moda muestral. Esas medidas nos van a permitir expresar mediante un valor único, el comportamiento del conjunto de datos que tenemos.

La media muestral, media aritmética, promedio o simplemente “la media” es una medida con la cual nos encontramos muy familiarizados en la vida cotidiana. Tenemos un conjunto de datos y simplemente los sumamos y los dividimos por la cantidad de valores que tenemos y eso nos da una idea del “comportamiento promedio de nuestros registros”. (Promedio = Sumatoria x/n). Dónde x representa el valor de cada dato y n el numero total de datos.

Si tomamos como ejemplo los valores aislados sin agrupar del Yo-Yo test de recuperación intermitente que vimos en la parte II del blog, podemos fácilmente calcular la media:

1240 1320 1480 1560 1600 1600 1640

1760 1840 1880 1880 1920 1920 1960

2000 2160 2160 2360 2360 2400 2560

2560 2600 2680 2800 2800 2840 2880

2920 2920 3000 3080 3160 3160 3240

Promedio = 80240 / 35 = 2292.6 m

Distancia recorrida Promedio = 2293 m

El promedio que calculamos, es una especie de “centro de gravedad” de la distribución de los datos. En este caso, si analizamos la siguiente figura, podemos observar que cada distancia recorrida durante el test realizado se halla representada por un punto, y que las distancias que se repitieron mas de una vez, poseen mas puntos. Las distancias de 1600, 1880, 1920, 1960, 2160, 2560, 2800, 2920 y 3160 tuvieron una frecuencia absoluta (fa)=2. Para que esa distribución permanezca equilibrada, el centro de gravedad se halla en 2293 m, que seria la media. El valor de la media, no es necesariamente un valor de una distancia recorrida realmente durante el test, sino el punto de equilibrio de las distribución.

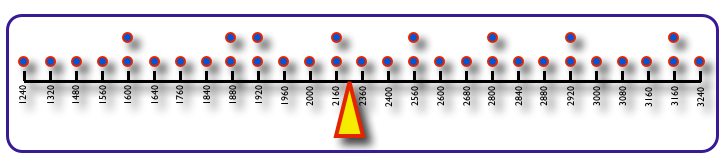
Figura 1. Representación gráfica de las distancias recorridas durante el tets Yo-Yo de recuperación intermitente nivel 1. Cada punto representa una distancia recorrida (m), y el triángulo al centro de gravedad de la distribución, la media.

El cálculo del promedio, es muy sensible a los valores extremos que podamos tener en una distribución de datos. Esto quiere decir que si tenemos uno o mas valores de distancia recorrida muy pequeños o muy grandes, eso repercutirá sobre el valor de la media y el centro de gravedad deberá desplazarse hacia derecha o izquierda para equilibrar la distribución.

Uso de la Media para Datos Agrupados en Intervalos

Ahora bien,

Si tuviéramos los datos agrupados por intervalos como en el blog anterior, cómo podemos proceder para calcular el promedio de la distancia recorrida durante el test?

En este caso, deberemos tener en consideración el numero de veces que se repite cada intervalo (fa) y multiplicarlo por lo que se denomina Marca de Clase o MC, que no es otra cosa que el promedio de cada intervalo (columna 3 de la Tabla):

MC = (Limite inferior del intervalo + Limite superior del intervalo) / 2

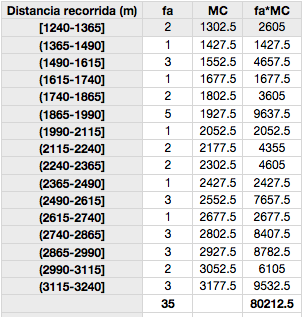
Tabla 1. Frecuencias absolutas (fa), Marcas de clase (MC) y productos de ambas variables (fa*MC) para cada intervalo de distancia recorrida (m) durante el Yo-Yo test de recuperación intermitente nivel I.

Una vez que tenemos la MC, multiplicaremos esa MC*fa, ya que tenemos que considerar el numero de veces que se repitió cada intervalo, por que no disponemos de los valores aislados.

Finalmente sumamos todas las MC*fa (columna 4, Tabla 1) y las dividimos por todas las fa (columna 2).

Por lo tanto, el promedio = 80212.5 / 35

Distancia recorrida Promedio = 2292 metros

Como observamos, es posible calcular el valor promedio tanto a partir de los datos sin agrupar como a través de los datos agrupados, siempre y cuando tengamos el dato de la frecuencia absoluta de cada intervalo.

Si tuviéramos que resumir las características de la media en términos de ventajas y desventajas, podríamos decir que su cálculo es ampliamente utilizado como medida de tendencia central, es muy sensible a cualquier variación que exista en los datos que registramos y que puede ser utilizada para otros cálculos estadísticos. Por otra parte, debido a que la media es una medida muy sensible a los valores extremos, no es recomendable utilizarla en aquellas distribuciones que sean muy heterogéneas, ya que obtendremos un valor que si bien es el centro de gravedad de la distribución, no representa el comportamiento real de gran parte de la distribución.

REFERENCIAS

Callegri-Jacques Sidia M (2008). Bioestadística. Principios y Aplicaciones. Editorial Artmed.

Di Rienzo JA, Casanoves F, Gonzalez LA, Tablada EM, Díaz MP, Robledo CW, Balzarini MG (2008). Estadística para las Ciencias Agropecuarias. 7 Edición, primera impresión. Editorial Brujas.

Vincent WJ (2005). Statistics in kinesiology. 3rd Edition. Human Kinetics.