Aplicación Biomecánica del Concepto de Fuerza en el Deporte y la Actividad Física

1.Introducción

Dentro de la cuantificación del movimiento deportivo según Gowitzke & Milner, (1981), Widule, C, (1994), Zatsiorsky V, (1994), Acero J. (2002) , Grabiner, M.(1993) y Nelson R. (1993) se establece una apertura muy estratégica por la diferencia entre describir un movimiento mismo e identificar las fuerzas que producen y controlan el movimiento. La descripción del movimiento sin consideración de las manifestaciones de las fuerzas generadoras es conocida como la cinemática. La valoración del movimiento con respecto a las fuerzas relacionadas es conocida como cinética. En otras, palabras nuestros movimientos son esencialmente de carácter cinemático y cinético.

Cuando nuestro cuerpo se mueve desde el ángulo de la cinemática cinco variables primarias son tenidas en cuenta: (1) las características temporales, (2) la posición o localización, (3) el desplazamiento o que movimiento ha ocurrido, (4) la velocidad o que tan rápido un cuerpo se mueve y (5) la aceleración o como la velocidad del cuerpo ha cambiado. La valoración de la cinemática del cuerpo humano puede ser vista en dos dimensiones (cinemática planar: x,y) tridimensionalmente (cinemática espacial: x,y, z) o en cuatridimensionalmente 4D (cinemática espacial: x,y, z y la integración del tiempo) (Acero, 2013)

La descripción del movimiento es un primer paso muy importante en concebir el movimiento humano pero esta está limitada a describir la geometría espacial del movimiento sin investigar las manifestaciones de las fuerzas que generan estos resultados. Debido a que la fuerza es el agente causal en el movimiento, la cinética es un área importante de consideración. Conceptos tales como: masa e inercia, fuerza, centro de masa y centro de gravedad, presión, torques, momentos de masa inercial, leyes del movimiento de Newton, equilibrio, trabajo y potencia, energía, colisiones, fricciones y fluidos son elementos fundamentales en el entendimiento del movimiento humano.

Ahora, las fuerzas que actúan en el sistema locomotor humano y que se relacionan con la actividad física y el deporte son las que permiten al ser humano realizar diferentes niveles de movimiento en términos de aceleración de masas, deformaciones de tejidos suaves y estructuras semirrígidas, para el desarrollo y crecimiento de los tejidos biológicos y para evitar o producir las lesiones por trauma o crónicas. Sin embargo, el término fuerza y sus contextos cinéticos deben ser aplicados más apropiadamente en el cuerpo humano y sus movimientos.

Nuestros cuerpos y los objetos que nosotros manipulamos están continuamente sujetos a fuerzas de diferente tipo. Esto permite al deportista o a la persona que realiza actividad física empezar movimientos, mantener la movilidad, parar, cambiar de dirección y permanecer en estados de balance y/equilibrio. Es por eso que la aplicación de las leyes del movimiento de Newton debe ser comprendida y utilizada analíticamente para entender el comportamiento de las fuerzas, como producir fuerzas resultantes, como resolver las fuerzas en sus componentes y como las fuerzas actúan en la resolución del equilibrio.

Usualmente en el entrenamiento deportivo y a la actividad física regulada se le dedica un tiempo importante a la preparación física de la denominada fuerza y sus diferentes manifestaciones y es por eso que se necesita entender más profundamente la importancia de la fuerza y su contexto cinético que tienen mucho que ver con la medición y la interpretación de los resultados. Una serie de artículos serán publicados a través de este portal con el fin de ilustrar científica y prácticamente esta parte de la biomecánica del movimiento

2.Concepto Fundamental de la Fuerza

Fuerza es una cantidad que no puede ser definida en si misma (Nigg, 2000) es igual que el tiempo, la masa, y la distancia sin embargo los efectos biológicos y mecánicos producidos por las fuerzas pueden ser descritos.

Si “algo” es capaz de mantener un resorte deformado, este “algo” es llamado una fuerza en un sentido estático. Si “algo” es capaz de acelerar una masa, este algo es llamado una fuerza en un sentido dinámico (Nigg, 1999). (Ver figura 1)

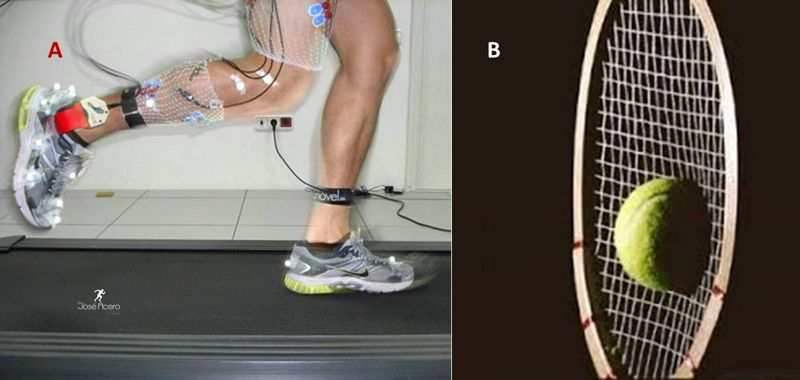
Figura 1. Ejemplos de los efectos de la fuerza. En el lado A se manifiesta un resorte deformado por compresión de una fuerza externa que lo mantiene. En el B el cuerpo (masa corporal) de este jugador es acelerado por su proceso interno neuromuscular hasta alcanzar su máxima distancia vertical

Existen dos formas de movimiento en el deporte en que se pueden visualizar los efectos de la fuerza: El empuje y el jalonamiento (halar). (Ver figura 2)

Figura 2. Ejemplos del empuje y jalonamiento encontrados en el deporte. En A el pitcher o lanzador traslada la bola empujándola hacia la dirección del lanzamiento. En B la judoka toma el Kimono de la contraria para realizar un jalonamiento o tracción de su masa corporal observado en las fases f2, f3 y f4

Entonces, de acuerdo con la anterior definición es por eso que en Biomecánica o Física la fuerza en si no se mide, se miden son sus efectos y por consiguiente la definición y la medición de la fuerza están más relacionadas con la determinación de sus efectos.

Los efectos biológicos pueden incluir el desarrollo de los tejidos, la contracción de los músculos, el crecimiento óseo o el movimiento de la sangre que son dados por el estímulo de las fuerzas aplicadas.

Los efectos mecánicos mayores producidos por la fuerza están relacionados (1) con la habilidad de acelerar una masa (por ejemplo cuando se golpea la pelota en el servicio de tenis (Ver figura 3) o se patea un balón en fútbol (Ver figura 4) y (2) con la habilidad de deformar un material cuando se comprime una plantilla en el zapato o se elonga un encordado en una raqueta de tenis. (Ver figura 5)

Figura 3. Ejemplo de un efecto mecánico de aceleración de una masa cuando se impacta la bola en el saque de tenis (240fps)

Figura 4. Ejemplo de un efecto mecánico de aceleración de una masa en el instante cuando se impacta la bola en el pateo en fútbol (5000 fps)

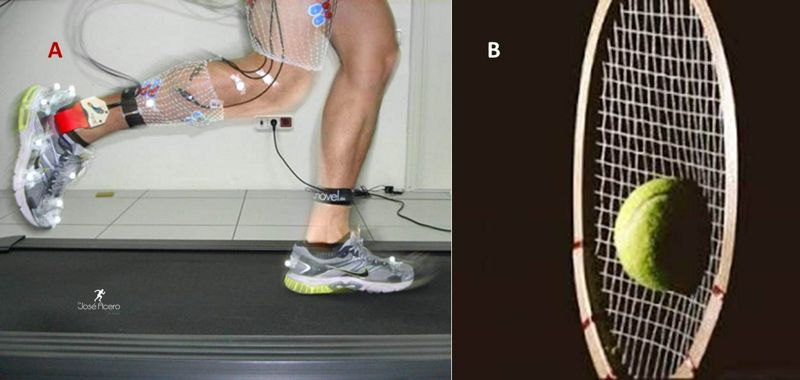
Figura 5. Ejemplo de la habilidad de deformación de un material. En A se observa cuando se impacta el piso en el trote y la plantilla del zapato es deformada por la fuerza 3D ejercida sobre ella. En B la deformación la experimentan tanto el encordado de la raqueta como la bola misma (1000fps)

3. Ecuaciones de los efectos de la fuerza

La segunda ley de Newton (para una masa constante) describe ecuacionalmente la habilidad de acelerar una masa como:

F = m*a (Ecuación 1)

Donde

F= Vector de la fuerza resultante actuando sobre m = masa del cuerpo

a = Vector de aceleración de la masa (efecto producido por F)

Con la unidad

[F] = [m]^*[a]

[F] = kg*m/s² = kg*m*s^{-2 =} N= Newton (Unidad de medida de la fuerza)

(Ver ejemplo en Figura 6)

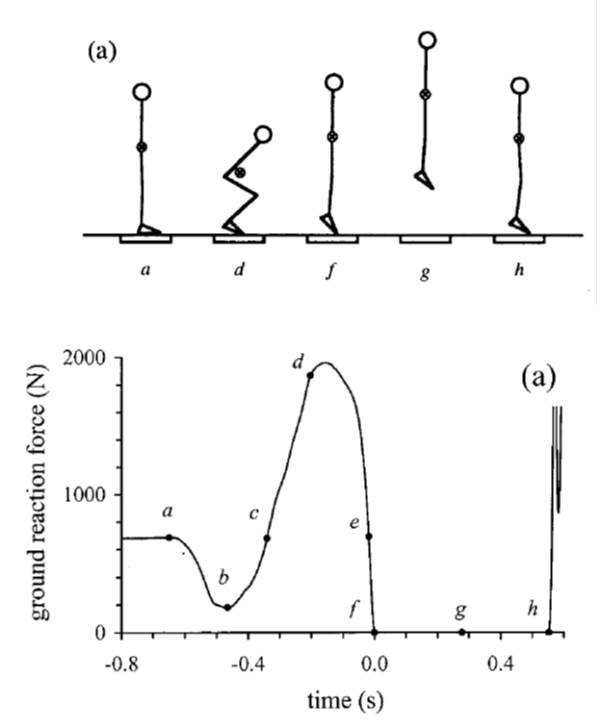
Figura 6. Cinco Fases del movimiento en un salto del tipo contra-movimiento (CMJ) y su correspondiente medición del efecto de la fuerza vertical (z) al acelerar (25 m/s/s) su masa corporal (75 kg) en sentido vertical. Las fase de mayor aceleración (d) fue de aproximadamente1875 N (75 Kg*25m/s²). Tomado y adaptado de Linthorne, 2001

Así también la habilidad de deformación de un material o tejido y tomado desde el caso más simple (Deformación de un resorte linear no en 3D). Las dos formas simples de deformar un cuerpo son la compresión y la tensión. Cada vez que nos ponemos de pie todo nuestro esqueleto es comprimido por efecto de nuestro propio peso. En forma similar si nos colgamos de una barra, son nuestros huesos y las articulaciones que los unen las que son tensionadas. Se obtiene lo siguiente:

F = k*∆x (ecuación 2) (ley de Hooke)

Dónde:

F= Vector de la fuerza resultante actuando sobre el resorte

k = Constante del resorte linear (descrito por la dureza (stiffness) del resorte) Módulo de Elasticidad o Módulo de Young

∆x = Deformación del resorte (cantidad vectorial). La cantidad de estiramiento (x) o de compresión (cambio de longitud), es directamente proporcional a la fuerza aplicada (F)

Con las unidades:

[F] = N

[k] = N/m y

[∆x] = m

(Ver ejemplo en Figura 7)

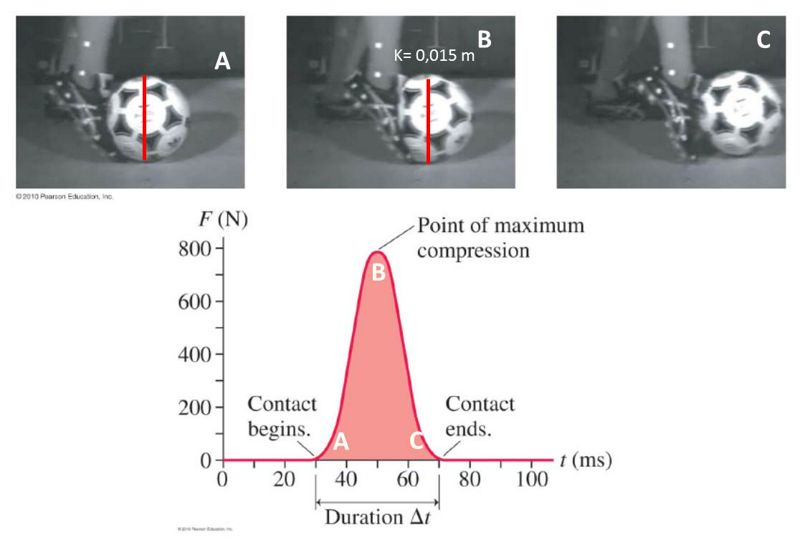
Figura 7. Deformación vertical del balón en el momento de máximo contacto con el pie en Futbol. En la fase B de máxima compresión F = 780N y la deformación del balón vertical fue de ∆x= 0,015 metros o 1.5 centímetros. Entonces averiguamos cual es la constante de elasticidad vertical del Balón (Modulo de Young). k= F/∆x= 780N/0,015m = 52000N/m

4. Referencias bibliográficas

Acero J. (2002) Bases Biomecánicas para la Actividad Física y Deportiva. Faid E

Acero J. (2013) Bases Biomecánicas para la Actividad Física y Deportiva ed. 3 Poemia editores. II&SB , ISBN 978-958-8705-60-6

Gowitzke B., and Milner M. (1981) Understanding the Scientific Bases of Human Movement. Williams & Wilkins, Baltimore USA.

Grabiner, M. (1993) Current issues in Biomechanics. Human Kinetics Publishers, Champaign USA,.Editores. Universidad de Pamplona - ISBN 958-97105-2-2

Linthorne N. (2001). Analysis of standing vertical jumps using a force platform. Am. J. Phys. 69 (11) November

Nelson R. (1993) Beyond Research-Solutions to Human Problems. The American Academy Of Physical Education .USA

Nigg B. (2000) Biomechanics and Biology of Movement. Forces acting on and in the human body. Ed. Human Kinetics. Champaign ILL. USA. Pgs. 253 -268

Widule, C. (1994) Biomechanical Foundations of Motor Skills. Learning Systems, West Lafayyette IN, USA.

Zatsiorsky V. (1994) Advanced Sport Biomechanics. The Pennsylvania State University, Biomechanics Laboratory, PA, USA