Cálculo de la potencia en función del tiempo: modelo matemático Peronnet–Thibault aplicado al ciclismo
Publicado 3 de julio de 2017, 14:22
Este blog es una traducción de Adrián Peris del trabajo "The Peronnet–Thibault mathematical model applied to the record power profile in cycling", escrito por J. Pinot* and F. Grappe.
1.Introducción
En el ciclismo, el nuevo concepto “record power profile” (RPP) permite la expresión del potencial físico del ciclista a través de la relación entre la potencia (de salida) (PO) y el tiempo (Pinot and Grappe, 2010, 2011). La PO desarrollada por un ciclista se está convirtiendo en una variable biomecánica del rendimiento, la cual es medida hoy en día diariamente en la bicicleta durante el entrenamiento y la competición. EL RPP puede ser un método innovador para el proceso de entrenamiento y para la evaluación de las diferentes capacidades físicas del ciclista (Pinot and Grape 2010).
En 1980, Peronnet and Thibault (1987, 1989) desarrollaron un modelo fisiológico del rendimiento en carrera. Su análisis proporciona una descripción de los récords del mundo en carrera. El modelo permite el cálculo de una medición objetiva del rendimiento: el índice de resistencia (IR). Ellos sugirieron que la pendiente de la relación entre el porcentaje de VO2max utilizado) y el tiempo de carrera de 7 minutos a 2 horas (expresado en escala logarítmica) puede ser un índice adecuado de la capacidad de resistencia (Peronnet and Thibault 1987, 1989). De hecho, mediante el procentaje de VO2max utilizado, es posible comparar la capacidad de resistencia y el nivel de rendimiento en corredores con diferente VO2ma . Por lo que nos preguntamos si podríamos obtener la misma relación al aplicar este modelo dentro de un rango más amplio de tiempo desarrollado por los ciclistas. Hasta donde sabemos, eso no se ha realizado todavía.
El propósito de este estudios es demostrar la relación entre la PO registrada expresada en función de la potencia aeróbica máxima (%PAM) y el tiempo (expresado en escala logarítmica) es similar al modelo matemático de Peronnet y Thibault.
2.Métodos
Durante la temporada competitiva de ciclismo (Febrero – Septiembre), 20 ciclistas realizaron sus entrenamiento y competiciones con un medidor de potencia (SRM Professional Training System, Schoberer Rad Messtechnik, Jülich, Germany) en sus bicicletas. Sus medias de edad, altura, peso y PAM eran 24±4 años, 178± 4cm, 67± 6kg y 6,4± 0,4 w/kg, respectivamente. Diez ciclistas eran miembros de equipos ciclistas profesionales. Los demás (n=10) eran élites y catalogados de primera categoría en Francia, seis de los cuales pertenecen al equipo nacional sub 23. Todos los ciclistas estaban orientados al alto rendimiento. Todos los datos se analizaron para determinar el RPP de los ciclistas. Los diferentes registros de PO (Power Output) corresponden a nueve registros de potencia media máxima (PMM) para tiempos de 5, 10, 20, 30, 45, 60, 120, 180 y 240 minutos. El RPP de un deportista corresponde a la relación entre las 9PMM y las diferentes duraciones, incluyendo todas las competiciones y entrenamientos durante un seguimiento longitudinal de la potencia en una temporada. La PO en el RPP se expresó según el peso corporal del ciclista (W/Kg). Hemos elegido el registro de Po en cinco minutos para expresar la PAM, a diferencia de Peronnet y Thibault (1897) que fijaron el tiempo sostenido a PAM (expresado en consumo máximo de oxígeno) en 7 minutos.
3.Resultados y discusión
La media del RPP de los 20 ciclistas expresada en w/kg en función a una escala logarítmica de tiempo representa una regresión lineal (El registro de potencia aeróbica disminuye linealmente entre 5 minutos y 4 horas de forma similar al modelo de Peronnet y Thibault (Pinnot and Grappe, 2010). El registro de potencia en 5 minutos (entre 5.5 y 7 w/kg) se aproximaba a la PAM evaluada en laboratorio con un test incremental máximo hasta la extenuación (Lucía et al 2001; Faria et al2005). El modelo de Peronnet y Thibault tiene en cuenta el rendimiento entre los 3000m y el maratón (entre 7 minutos y 2-3 horas). En ciclismo, la duración media de las carreras profesionales es de entre 5 y 7 horas. En nuestra muestra ciclista, la mitad son de élite y las carreras no superan las 5 horas. Por lo tanto, cogimos datos de potencia hasta 4 horas.
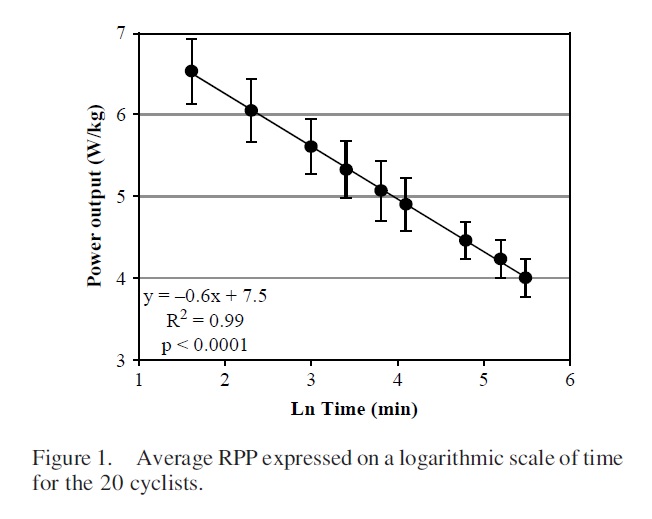
Figura 1. RPP medio expresado en una escala logarítmica de tiempo de los 20 ciclistas.
Nuestro modelo permite la representación del potencial aeróbico de los ciclistas en función de una regresión lineal siguiendo la siguiente ecuación:
PO = -0.6 ln T + 7.5 (con ln T = logaritmo neperiano del tiempo de pedaleo en minutos)
Si la disminución de potencia (entre 5 minutos y 4 horas) se convierte/trasforma en la disminución del porcentaje de utilización de la PAM, la relación es también regresión lineal (Figura 2). Por lo tanto, la relación es similar a la observada por Peronnet y Thibault en las mediciones de velocidad realizadas con corredores.
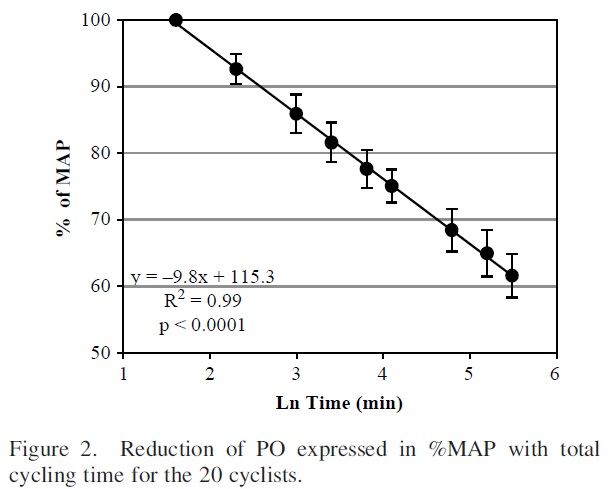
Figura 2. Reducción de PO expresada en % de la potencia aeróbica máxima en función del tiempo en 20 ciclistas.
Una definición empleada generalmente para la capacidad de resistencia es la habilidad para disminuir la pérdida de potencia con el incremento de la duración del ejercicio (Peronnet y Thibault 1987). Por lo tanto, nuestros resultados sugieren que la pendiente de la regresión lineal entre la potencia registrada y el ln T podría ser un índice de la capacidad de resistencia en el ciclismo.
El índice de resistencia medio encontrado en nuestro estudio es de -9,8, el cual no corresponde exactamente con los valores del índice de Peronnet y Thibault encontrado con los corredores (-4 a -8).
Un estudio futuro abordará el análisis del índice de resistencia en ciclistas con diferentes capacidades y nivel competitivo.
4.Conclusiones
Los resultados de este estudio muestran a través de un seguimiento longitudinal de los datos de potencia de un grupo heterogéneo de ciclistas que la relación entre el porcentaje de la PAM utilizado (según el registro de PO) y el tiempo (expresado en una escala logarítmica) es lineal. Por lo tanto, el modelo de Peronnet y Thibault parece ser adecuado para determinar un índice de resistencia a partir relación lineal entre los diferentes valores de potencia.
