Efecto del Ciclo Estiramiento-Acortamiento Muscular Prolongado sobre el Recobro de Energía Elástica y el Gasto Energético

El aumento del rendimiento en ejercicios con ciclo estiramiento-acortamiento ha sido atribuido al recobro de energía elástica almacenada durante la fase de estiramiento. Si el tiempo entre la fase de estiramiento y acortamiento (tiempo de acoplamiento) es demasiado largo, la energía almacenada se puede perder. En el presente estudio, el tiempo de acoplamiento fue incrementado pidiéndole a 10 sujetos que corrieran en una cinta ergométrica a diferentes velocidades (2,2 – 5,2 m.s-¹), los sujetos usaron calzado especial blando así como también calzado común. Los resultaron indicaron que correr con calzado blando requirió un consumo de energía mayor que correr con calzado común, excepto a velocidades bajas (2,2 m.s-¹). La energía extra consumida con el uso de calzado blando se incremento de forma paralela cuando la velocidad de carrera fue aumentada (0,4 J.kg-¹/paso a 5,2 m.s-¹). Fue sugerido que el efecto del tiempo de acoplamiento como un factor limitante para el recobro de energía elástica fue relevante en las fibras de contracción rápida (FT), que fueron reclutadas progresivamente cuando la velocidad de carrera fue incrementada. Esto es consistente al hecho de que el tiempo de vida de los puentes cruzados en las fibras FT es muy corto, y de este modo más sensible al tiempo de acoplamiento. A velocidades de carrera bajas (2,2 m.s-¹) solo fueron reclutadas las fibras de contracción lenta (ST) y el incremento del tiempo de acoplamiento no fue lo suficientemente largo para provocar una separación de los puentes cruzados de las fibras ST, las que poseen un tiempo de vida largo de los puentes cruzados. Fue concluido que los diferentes reclutamientos de fibras ST y FT influenciaron los patrones de recobro de energía elástica, los cuales dependieron de la velocidad de carrera.

INTRODUCCIÓN

Ha sido demostrado que el estiramiento de un músculo activado incrementa su rendimiento durante un trabajo posterior positivo. Esto ha sido atribuido al recobro de energía elástica que produce una cierta cantidad de trabajo mecánico sin la utilización de energía química (Cavagna et al. 1965, 1976; Cavagna & Kaneko 1977; Asmussen & Bonde-Petersen 1974). Sin embargo si el tiempo entre al estiramiento y el acortamiento (tiempo de acoplamiento) es muy largo, la energía elástica almacenada puede perderse (Cavagna et al.1968, Bosco 1982). Así, el tiempo de acoplamiento juega un rol esencial en la economía del trabajo muscular. Ha sido demostrado que la duración del tiempo de acoplamiento está relacionado a la duración de la fase de estiramiento y al tiempo total del ciclo estiramiento-acortamiento (Bosco et al. 1982 a,b).

Los experimentos con humanos han demostrado que un tiempo de acoplamiento voluntariamente prolongado en ejercicios de saltabilidad con rebotes reduce marcadamente el efecto de potenciación pre-estiramiento (Margaria et al. 1963, Thys et al. 1972, Asmussen & Bonde-Petersen 1974, Bosco et al. 1982 a).

Para examinar este fenómeno la duración del tiempo de acoplamiento fue incrementada, no voluntariamente, sino a través de la prolongación del ciclo estiramiento-acortamiento total. Ha sido demostrado que la carrera causa una disminución de la fuerza del cuerpo que colisiona, aumentando el tiempo de colisión (Mc Mahon & Green 1979). De este modo correr en superficies blandas podría provocar una prolongación del ciclo estiramiento-acortamiento de los músculos extensores, que consecuentemente aumenta el tiempo de acoplamiento. Esto debería disminuir la cantidad de trabajo mecánico realizado sin contribución de energía química. En el presente estudio esta hipótesis fue verificada comparando el costo energético de carreras en estado estable realizadas en cinta ergométrica usando calzado común y calzado especial blando.

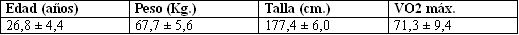
Tabla 1. Valores medios y desvíos estándar de las características físicas de todos los sujetos (n = 10) examinados.

MÉTODOS

La muestra de este estudio estuvo formada por 10 sujetos varones del staff de la universidad. Los sujetos estaban familiarizados con la carrera en cinta ergómétrica y poseían altos consumos máximos de oxígeno (V02 máx.). Sus características físicas están presentadas en la Tabla 1.

Cada sujeto corrió 12’ en la cinta ergométrica, con calzado común y blando durante dos días diferentes. Durante el primer día la velocidad de la cinta fue ajustada inicialmente a 8 km/h, se incrementaba luego de 4’ a 12 km/h y de nuevo después de 4’ a 15 km/h. Luego de 30-40’, los sujetos hacían exactamente lo mismo solo que se cambiaban el calzado. Durante el segundo día fue usado el mismo protocolo excepto que las velocidades de carrera fueron cambiadas (12, 15, y 18 km/h o 8,15 y 20 km/h). La carrera a la mayor velocidad era seleccionada de acuerdo al máximo consumo de oxígeno de cada sujeto, que había sido medido en un estudio previo. Las zapatillas fueron preparadas por los investigadores, ya que el peso de las zapatillas blandas (Adidas, con un material visco-elástico especial) fue de 530 g, un peso extra (200 g) fue adicionado a la parte dorsal de las zapatillas comunes (330 g).

El consumo de oxígeno fue medido cada 30’’, utilizando un sistema automático (Mijnhardt, Oxygon-4), que fue calibrado antes y después de cada test con concentraciones de gas conocidas. El valor del estado estable fue calculado como una media de las 4 últimas determinaciones de 30’’. La reproductivilidad test-retest de las mediciones fue chequeada comparando los valores de gasto energético (E exp) para la misma velocidad y para las mismas condiciones (calzado común y blando) en días diferentes (r = 0.98, p< 0,001). Fueron tomadas muestras de sangre para la determinación de la concentración de lactato (método enzimático, Biochemica, Boehringer) luego de las carreras a la mayor velocidad. Debido al incremento del lactato sanguíneo más allá de 4 mmol.l-¹, algunas de las velocidades de carrera más altas no fueron incluidas en los resultados finales. La frecuencia de pasos fue calculada contando el número de pasos ejecutados en 30’’ en una cinta ergométrica común. Una cinta ergométrica especial con una plataforma de fuerza colocada debajo de la cinta fue usada para medir el tiempo de contacto del pie durante la carrera a diferentes velocidades en 4 sujetos. La frecuencia cardiaca fue calculada a través de mediciones electrocardiográficas al final de cada minuto.

RESULTADOS

La frecuencia media de pasos de los sujetos se incrementó desde 2,5 a 2,8 Hz, cuando la velocidad de carrera fue incrementada de 8 km/h (2,2 m.s-¹) a 18 km/h (5 m.s-¹). La Fig. 1 muestra también la frecuencia de pasos media a la más alta velocidad individual de carrera en condiciones de estado estable (18,6 km/h o 5,16 m.s-¹). No fueron observadas diferencias cuando los dos tipos de carreras (con calzado común o blando) fueron comparadas. En contraste, el gasto energético demostró un patrón diferente cuando se usaron los dos tipos de calzado. El costo energético expresado en J.kg-¹ y por km fue similar para las dos condiciones a la velocidad de carrera más baja (Fig, 2). Sin embargo, cuando la velocidad de carrera fue incrementada, el E exp. Fue más alto cuando se corría con calzado blando en comparación que cuando se corría con calzado común. La diferencia en el costo energético (∆ E exp.) entre los dos tipos de locomoción fue estadísticamente significativa desde los 3,3 m.s-¹ (Test t de Student, t = 2,15, p< 0,05, datos apareados), y las diferencias se hicieron más significativas cuando la velocidad de carrera fue incrementada. La misma figura muestra que la diferencia en la frecuencia cardiaca entre las dos condiciones siguió patrones similares al ∆ E exp. Los valores promedio de las diferencias en el costo energético cuando se uso calzado blando calculado por paso, es presentado en función de la velocidad de carrera en la Fig. 3.

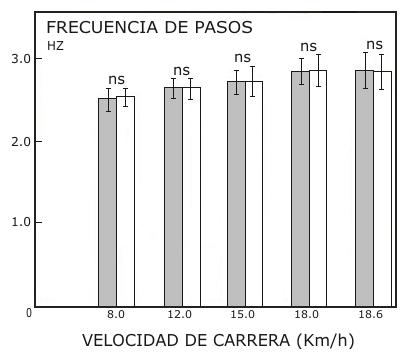
Figura 1. Frecuencia de pasos media (± SD) durante la locomoción con calzado normal (barras ralladas) y calzado blando (barras vacías) medida a diferentes velocidades de carrera. El valor presentado del lado derecho representa la velocidad más alta estudiada de cada individuo. ns = no-significativo (test t de Student, observaciones apareadas).

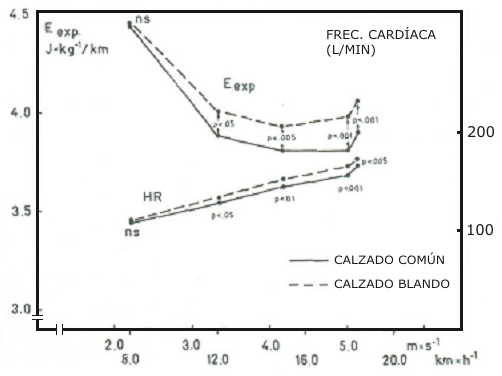
Figura 2. El gasto energético (E exp.) por kilogramo y por kilómetro de todos los sujetos estudiados durante la locomoción con calzado común (línea completa) y con calzado blando (línea cortada) es presentado en función de la velocidad de carrera. También es presentada la frecuencia cardiaca. ns = no-significativo (test t de Student, datos apareados).

DISCUSIÓN

La fisonomía biomecánica de la carrera no cambio cuando se utilizo calzado blando. Esto puede ser demostrado por el hecho de que la diferencia de pasos fue la misma, cuando fue comparada la locomoción con los dos tipos de calzado (Fig. 1). De otro modo, la Fig.2 demuestra claramente que correr con calzado blando requiere un gasto energético mayor (E exp.) que la locomoción con calzado normal. En orden de explicar esto, las siguientes consideraciones deberían ser tenidas en cuenta.

Ha sido demostrado que el costo energético de la carrera por unidad de distancia es independiente de la velocidad (Boje, 1944; Margaria et al. 1963, Ito et al. 1982). Los presentes resultados concuerdan con aquellos hallazgos, excepto porque el gasto energético medido a la velocidad más baja de 2,2 m.s-¹ (8 km/h) fue mayor que a velocidades más altas. Una posible explicación para este fenómeno es que los sujetos con una aptitud física extremadamente alta, encontraron a la velocidad más baja como inusual comparada con su velocidad usual de entrenamiento. No obstante, los presentes resultados son similares a aquellos reportados por Fellingham et al. (1979).

Ha sido observado que la influencia mecánica durante la carrera es más alta (45 a 75 %) (Cavagna et al. 1964, Cavagna & Kaneko 1977, Ito et al. 1982), que la eficiencia máxima (25 %) del componente contráctil del músculo (eg. Dickenson 1929). Esto ha sido atribuido al almacenamiento de energía elástica en el músculo durante el trabajo excéntrico (fase de amortiguación) y su re-uso en forma de trabajo mecánico durante la fase de acortamiento (fase de empuje). En el presente experimento el costo energético por unidad de distancia fue similar al reportado anteriormente. Así, aún a velocidades bajas (2,2 m.s-¹) una cierta cantidad de energía elástica parece ser utilizada.

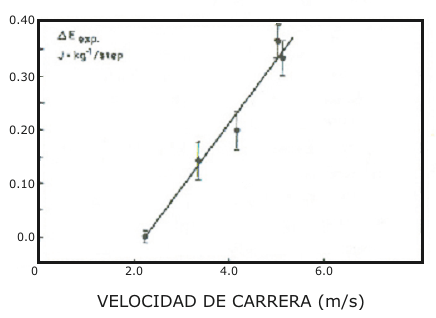
Figura 3. Gasto energético extra (∆ E exp.) promedio (± SE) durante el ciclo de pasos causado por la locomoción con calzado blando en función de la velocidad de carrera.

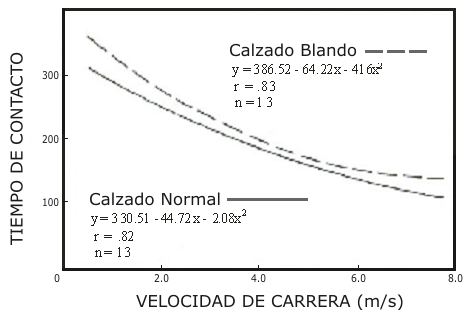
Figura 4. Relación entre el tiempo total de contacto en el suelo durante la locomoción con calzado blando (línea cortada) y común (línea completa) y la velocidad de carrera. Las dos curvas están basadas en trece observaciones realizadas por 4 sujetos que corrieron en una cinta ergométrica especial, que tenía una plataforma de fuerza debajo de la cinta, a velocidades similares a las cuales fue medido el E exp.

La locomoción realizada con calzado blando implica, como es esperado, un E exp. mayor comparado con el rendimiento con un calzado común. Esto sugiere que el hecho de correr con calzado blando modifico intensamente el comportamiento mecánico de los músculos extensores de las piernas, incrementando probablemente el período de transición (tiempo de acoplamiento) entre el estiramiento y el acortamiento. Esta suposición es sostenida por el hecho de que correr con calzado blando demostró un incremento en el ciclo estiramiento-acortamiento total durante el período de contacto (ver Fig. 4), y es sabido que el Ct está linealmente relacionado a este ciclo (Bosco et al. 1981, Bosco 1982 c).

Así el incremento del Ct podría haber favorecido la separación de los puentes cruzados del músculo y la consecuente perdida de energía elástica. No fue observada ninguna diferencia a velocidad baja entre las dos condiciones de carrera. Aparentemente esto puede sugerir que a muy baja velocidad de locomoción (2,2 m.s-¹) el almacenamiento y recobro de energía elástica no ocurre, tanto si es utilizado un calzado blando como uno común. De otro modo, ha sido presentada evidencia de que el trabajo extra es realizado por el re-uso de fuerza elástica aún a baja velocidad. De este modo, en orden de investigar los mecanismos posibles que expliquen estos hallazgos otros resultados también necesitan atención. Correr a baja velocidad (2,2 m.s) implica bajas velocidades angulares de estiramiento-acortamiento, así como el desarrollo de bajos niveles de fuerza promedio durante contracciones concéntricas y excéntricas (Bosco & Rahkila, en preparación). Esto favorece el reclutamiento de fibras de contracción lenta (ST) (eg. Henneman et al. 1965, Tanji & Kato 1973, Gydikov & Kosarov 1974, Bosco et al. 1982 c) que poseen un tiempo largo de unión de los puentes cruzados (eg. Goldspink et al. 1970, Goldspink 1978). De este modo, aún si el tiempo total de contacto con el suelo fue aumentado cerca de 20 ms de ≈ 240 ms (calzado normal) a ≈ 260 ms (calzado blando), el consecuente incremento en el Ct no fue tan largo para limitar el recobro de energía elástica durante la locomoción con calzado blando. Esta suposición es corroborada por hallazgos recientes (Bosco et al. 1982 c) que apoyan la hipótesis de que el largo tiempo de acoplamiento favorece a las fibras ST para que retengan su energía elástica más tiempo sin que se separen los puentes cruzados (Bosco 1982). Esto fue observado en saltos en los cuales el ciclo estiramiento-acortamiento total fue aún más largo (≈420 ms) que el tiempo total de contacto en la carrera (< 300 ms) en el presente estudio. Como era esperado el tiempo de contacto en el suelo decrecía a medida que la velocidad de carrera aumentaba en las dos condiciones examinadas (calzado normal y blando), la evidencia es la presentada en la Fig. 4. La duración del Ct también es sensible a disminuir, ya que la duración del Ct está relacionada al tiempo del ciclo estiramiento-acortamiento (Bosco et al. 1981). Esta suposición es sostenida por hallazgos de Ito et al. (1982), que observó una disminución del Ct desde 12 ms a 4 ms, cuando la velocidad de carrera fue cambiada de 2 a 6 ms-¹. Ellos concluyeron, que debido a que el Ct era muy corto, su influencia en el recobro de energía elástica fue pequeña. Esto no parece estar sostenido por los presentes hallazgos, debido a que pequeños incrementos del Ct, cuando se uso calzado blando incremento significativamente el E exp. en las carreras a velocidades más altas que 2,2 m.s-¹. Esto sugiere que aún un pequeño aumento en el Ct limita substancialmente el tiempo de recobro de energía como fue demostrado en la Fig. 3. Los presentes hallazgos están sostenidos por los resultados de Bosco et al. (1981), que observó que 1 ms de incremento en el Ct correspondió a 20 N de disminución en el efecto de potenciación debido al preestiramiento en los saltos.

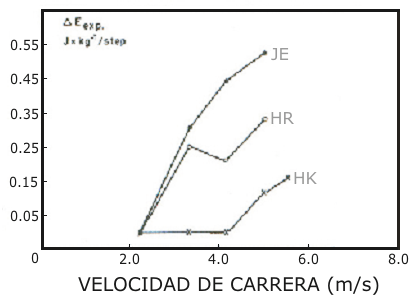
Figura 5. Gasto energético extra (∆ E exp.) durante el ciclo de pasos, causado por la locomoción con calzado blando en función de la velocidad de carrera para tres sujetos, cuyas composiciones musculares de fibras en el músculo vasto lateral eran conocidas.

Como fue antes discutido, el tiempo de contacto en el suelo y consecuentemente el Ct a todas las velocidades de carrera estudiadas fue demasiado corto para ser un factor limitante del recobro de energía elástica en las fibras ST. De este modo, es sugerido que el efecto limitante del tiempo de acoplamiento en el recobro de energía elástica es relevante en las fibras de contracción rápida (FT) (Bosco et al. 1982 c). Esto es consistente con el hecho de que el tiempo de vida de los puentes cruzados en las fibras FT es muy corto (Barany 1967, Goldspink et al. 1970, Goldspink 1978). En esta conexión es interesante notar que el costo de energía extra expresado por ciclo de pasos, aumento a medida que la velocidad de carrera fue incrementada. De este modo, el efecto del Ct como un factor limitante para el re-uso de energía elástica debe haber aumentado en función de la velocidad y de la energía elástica almacenada en las fibras FT. Parece que el almacenamiento fue extendido a un mayor número de puentes cruzados como consecuencia de la mayor fuerza desarrollada por el ciclo estiramiento-acortamiento de los pasos, más largo. Esto es substancial por el hecho de que la magnitud de energía elástica almacenada durante el trabajo excéntrico depende de la fuerza desarrollada al final de cada estiramiento (Bosco et al. 1981). En una serie de estudios paralelos (Bosco & Rahkila en preparación; Bosco observación no publicada) fue observado que el desarrollo de fuerza al final del ciclo excéntrico de cada paso fue aumentado de 14,6 N.kg de peso corporal-¹ a 22,9 N. N.kg de peso corporal-¹ a medida que la velocidad de carrera aumentaba de 2 a 5 m.s-¹.

Finalmente, Flitney & Hirst (1978) sugirieron que durante la fase de estiramiento parte del desarrollo de la tensión es tomada por los elementos elásticos que se disponen en serie con los sarcómeros. Esto puede ocurrir rotando las cabezas de miosina hacia atrás en contra de su tendencia natural de mantenerse en una posición de energía potencial más alta.

De hecho esto significa almacenamiento de trabajo mecánico en los puentes cruzados del sarcómero. Así los presentes resultados apoyan la idea de que durante movimientos balísticos la contribución de las fibras FT se hace progresivamente más importante para la producción de fuerza a medida que se incrementa la velocidad del ciclo estiramiento-acortamiento (Gillespie et al. 1974, Smith et al. 1977).

Quizás uno de los hallazgos más importantes del presente estudio fue el descubrimiento de que el costo energético debido al uso de calzado blando fue marcadamente diferente entre los sujetos estudiados, y esto parece ser sensible a la distribución de los tipos de fibras en el músculo y al V02 máx. La Fig. 5 muestra los resultados de tres sujetos que poseían diferentes porcentajes de fibras ST en sus músculos vasto lateral, así como diferentes V02 máx. 82 ml.kg-¹.min-¹ y 62 % de ST para el sujeto HK, 70 ml.kg-¹.min-¹ y 53 % de ST para el sujeto HR y 60 ml.kg-¹.min-¹ y 50 % de ST para el sujeto JE, respectivamente (el V02 máx. y la distribución de fibras habían sido determinados en otro estudio con otros fines). Asumiendo que la locomoción con calzado blando incrementa el tiempo de acoplamiento durante el ciclo de pasos, y que su poder limitante se extiende solo a las fibras FT durante el ciclo estiramiento-acortamiento (< 300 ms), entonces puede ser posible estimar el reclutamiento selectivo de las fibras musculares FT durante diferentes velocidades de carrera. Los resultados de la Fig. 5 sugieren que en el sujeto HK podría haber ocurrido un reclutamiento substancial de las fibras FT no antes de los 5 m.s-¹. De otro modo, para los dos sujetos HR y JE el envolvimiento de las fibras FT podría haber ocurrido ya a baja velocidad (3,3 m.s-¹). Esta observación es consistente con estudios en los cuales fue estudiada la utilización de glucógeno (eg. Gollnick et al. 1974). Recientemente Essen (1978) demostró que durante un ejercicio de ciclismo aproximadamente al 50-60 % del V02 máx. fueron involucradas las fibras FT, y la magnitud de este efecto dependió de la distribución de las fibras de los sujetos. El sujeto HK, con un VO2 máx. alto, fue capaz de realizar un trabajo mecánico más grande a través del reclutamiento de las fibras ST, que los otros dos sujetos, que poseían VO2 máx. más bajos.

Esto sugiere que el VO2 máx. es otra característica fisiológica que influencia los patrones de reclutamiento de las fibras musculares a niveles submáximos (eg. Skinner & Mc Lellan 1980). Sin embargo, debe saberse que a pesar de que han sido observados resultados similares en otros sujetos en los cuales el VO2 máx. y la distribución de fibras eran conocidos, debido al número limitado de sujetos, estos hallazgos no permiten hacer ninguna generalización y son necesitados más estudios para llegar a una conclusión.

Este estudio fue respaldado por una subvención del Ministerio de Educación (Finlandia).