Energética en Carreras a Pie de Kilómetro Vertical; ¿Cuánto más Inclinado Mejor?
Nicola Giovanelli1,2,3, Amanda Louise Ryan Ortiz3, Keely Henninger3 y Rodger Kram3
1Department of Medical and Biological Sciences, University of Udine, Udine, Italy
2School of Sport Sciences, University of Udine, Udine, Italy
3Locomotion Laboratory, Integrative Physiology Department, University of Colorado, Boulder, Colorado
Artículo publicado en el journal PubliCE del año 2016.
Publicado 22 de diciembre de 2016
Giovanelli N, Ortiz AL, Henninger K, Kram R. Energética en carreras a pie de kilómetro vertical; ¿cuánto más inclinado mejor? J Appl Physiol 120: 370–375, 2016. First published November 25, 2015; doi:10.1152/japplphysiol.00546.2015.— Los kilómetros verticales son carreras a pie que consisten en un desnivel positivo de 1000m en recorridos menores a 5000m, siendo de unos 30º las pendientes de las carreras más rápidas. Estudios previos se han centrado de una manera superficial en la inclinación y en la técnica de subida en pendientes. El objetivo de este estudio es el de cuantificar el costo metabólico de caminar y correr en inclinaciones con bastante pendiente y distinguir biomecánicamente caminar de correr. 50 corredores (10 hombres, 5 mujeres, 32.9 ± 7.5 años, 1.75 ± 0.09 m, 64.3 ± 9.1 kg) caminaron y corrieron durante 5 min en 7 inclinaciones diferentes (9.4, 15.8, 20.4, 24.8, 30.0, 35.0, y 39.2°) todos a una velocidad vertical fija (0.35 m/s). Se midió la tasa metabólica y se calculó el gasto vertical de caminar (Cwvert) y de correr (Crvert). Usando un vídeo-análisis, se determinó la frecuencia de zancada, la longitud de zancada y el duty factor (fracción de cada zancada que cada pie está en contacto con el suelo). En todas las inclinaciones excepto 9.4º, Cwvert fue más económico que Crvert (media -8.45 ±1.05%; P < 0.001). Además, la mínima diferencia para Cwvert y Crvert existió entre 20.4 y 35.0º (media de Cwvert 44.17±0.41 J·kg-1·m-1 y media de Crvert 48.46±0.35 J·kg-1·m-1). En todas las inclinaciones y velocidades evaluadas, tanto caminando como corriendo se tenía al menos un pie en el suelo todo el tiempo. Sin embargo, caminando, la frecuencia y la longitud de zancada fueron »28% más lenta y larga, respectivamente, que corriendo. En conclusión, se halló que hay un rango de inclinaciones para que el gasto de energía sea minimizado. A la velocidad vertical evaluada, en inclinaciones mayores a 15.8º, los corredores pueden reducir su gasto energético caminando más que corriendo.
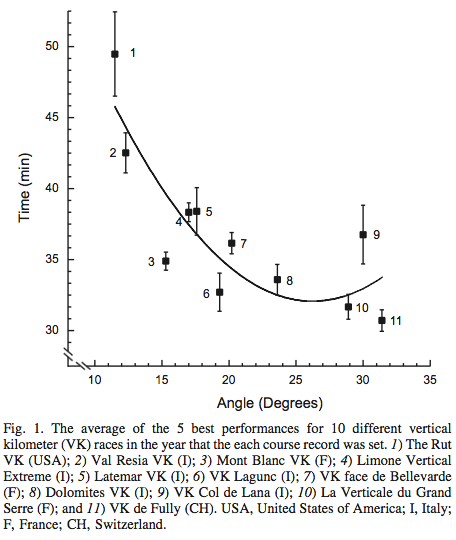
En carreras a pie de kilómetro vertical (VK), los corredores completan 1000m de desnivel positivo en una distancia total de hasta 5000m (International Skyrunning Federation rules: http://www.skyrunning.com. El terreno, la pendiente y la distancia varía entre las diferentes carreras. Hasta la fecha, el record mundial para hombres en VK es de 29 min y 42 s, establecido en una carrera de 1.920 m y una inclinación media de 31.4º (Km Vertical de Fully, Switzerland). Esto equivale a una velocidad en el plano vertical de ±0.56 m/s y una velocidad en paralelo al suelo de 1.08 m/s. Un carrera de VK con una escasa inclinación requeriría una excesiva velocidad en horizontal. Por ejemplo, una carrera con una inclinación de sólo 1º requeriría una velocidad de carrera imposible de 31.83 m/s para subir 1.000 m en 30 min. A la inversa, una carrera con una inclinación de 40º necesitaría de una velocidad de sólo 0.87 m/s para alcanzar 1.000 en 30 min. No obstante, si la carrera es demasiado inclinada, se requerirían técnicas de alpinismo que probablemente son más lentas que correr o caminar en pendientes más moderadas. El análisis de los mejores rendimientos en diferentes carreras de VK sugieren que podría haber una inclinación óptima para conseguir el mejor tiempo (Fig. 1). Como no hay carreras de VK con una inclinación media superior a 31.4º (Km Vertical de Fully), no se sabe si la inclinación óptima podría ser verdaderamente mayor.
Otro factor a considerar es que en las carreras de VK, algunos corredores caminan, otros corren y otros van alternando el paso. No está claro qué paso o que combinación es la óptima. En llano o en cintas de correr, a velocidades menores a alrededor de 2.0 m/s, caminar requiere de un gasto metabólico menor que correr (3, 15, 17, 25). Esto es generalmente atribuido a un intercambio pendular más efectivo a nivel de energía mecánica en velocidades más bajas caminando, y al almacenamiento y el retorno de la energía elástica a velocidades más altas corriendo (6). Sin embargo, en inclinaciones cuesta arriba ambos mecanismos están mermados (8, 24). A nivel del suelo (17) así como en moderadas pendientes hacia arriba y hacia abajo (18, 19), la velocidad de transición caminar-correr preferida ocurre cerca pero no exactamente en la velocidad de transición óptima metabólicamente. Como la velocidad aumenta, la gente normalmente adopta primero un paso de carrera a una velocidad más lenta que el punto de cruce metabólico.
El coste metabólico de caminar cuesta arriba y correr ha sido de gran interés en la fisiología del ejercicio (3, 14, 15, 18), pero casi todos los estudios han examinado caminar y correr cuesta arriba en pendientes <9º. Una excepción destacable es el innovador estudio de Minetti et al. (21). Midieron el coste metabólico (J·kg-1·m-1) de caminar (Cw) y de correr (Cr) en un rango de pendientes de hasta 24º. Las distancias calculadas para Cw y Cr fueron similares al exterior y a la cinta de correr. Ellos concluyeron que a una velocidad dada en cinta de correr, Cw y Cr eran directamente proporcionales a la pendiente +15% (8.5º) y que Cw y Cr convergían en inclinaciones mayores. Minetti et al. (21) también definieron el coste vertical de caminar (Cwvert) y de correr (Crvert) como la energía gastada para ascender un metro vertical. Cwvert y Crvert decrecían a inclinaciones mayores llegando a valores mínimos en rango del 20% (11.3º) al 40% (21.8º). No obstante, nosotros somos reacios a extrapolar los datos de Minneti et al. a pendientes más empinadas que son lo que están presentes habitualmente en las carreras de VK. Además, los corredores de VK, cuando van a la misma velocidad alternan a menudo entre caminar y correr, y Minetti et al. no hicieron comparaciones directas entre la energética de correr y caminar a las mismas velocidades. Finalmente, no está claro si la distinción biomecánica tradicional entre caminar y correr en llano (p.e., corriendo, la trayectoria del centro de masas llega a su punto más bajo en la fase intermedia de apoyo y hay una fase aérea cuando los pies no está en contacto con el suelo) se aplique en pendientes muy pronunciadas. En investigaciones previas se ha usado el término “Groucho running” (16) (marcha de Groucho) y “grounded running” (23) (correr a ras de suelo) para describir el paso que no implica una fase aérea.
En nuestro conocimiento, no hay estudios científicos previos que hayan estudiado las inclinaciones caminando y corriendo en las carreras de VK más rápidas. Minetti et al. (20) analizaron carreras de correr escalones, pero las carreras en las que se corre subiendo rascacielos son mucho más cortas de las carreras de VK (desde 50 s a unos 14 min).
El principal objetivo de este estudio fue cuantificar el coste metabólico de caminar y correr a través de un amplio rango de inclinaciones hasta y más allá de los que se usan en las carreras de VK. Nuestro propósito fue determinar si caminar o correr es más económico y si hay unas inclinaciones óptimas para los dos tipos de paso. Comparamos caminar y correr a una velocidad vertical fija (0.35 m/s) en un rango de inclinaciones desde »10º a »40º. Basándonos en hallazgos de Minetti et al. (21), y a causa de que las velocidades estudiadas sobre la cinta de correr fueron <2.0 m/s, hipotetizamos que: 1) caminar requeriría menos energía metabólica que correr y más allá hipotetizamos que 2) para caminar y correr, habría distintas pendientes intermedias (»30º) que minimizarían el coste energético de ascender a una velocidad vertical fija.
Nuestro propósito secundario fue distinguir la biomecánica de caminar y correr cuando hay pendiente. Nosotros hipotetizamos que 3) en pendientes y a bajas velocidades en cinta, correr no involucraría una fase aérea. Sin embargo, una mayor frecuencia de zancada durante la carrera podría distinguirla de caminar.
MATERIALES Y MÉTODOS
Sujetos. 15 corredores en buen estado de salud que compiten en carreras por montaña (10 hombres y 5 mujeres 32.9±7.5 años, 1.75±0.09 m, 64.3±9.1 kg) se presentaron voluntarios y dieron su consentimiento informado para la University of Colorado Institutional.
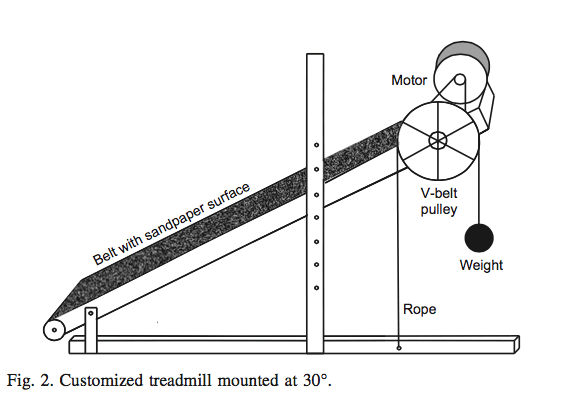
Diseño experimental. Nosotros adaptamos la cinta rodante para las inclinaciones de 0 a 45º. Para dar una tracción adecuada, nosotros adherimos unas franjas que mejoraban la sujeción (p.e. papel tipo lija) a la cinta de correr (Vicious Tape, Vancouver, BC, Canada).
Para proteger el control motor electrónico, montamos unas poleas como cinturones en el rodillo de la cinta, colgados con cuerdas de las poleas y atados pesos moderados a las cuerdas (»8 kg). Elegimos la mínima cantidad de peso de tal manera que cuando el sujeto permaneciera en la cinta rodante con el motor apagado, el cinturón no se moviese. Proveer una resistencia mecánica al motor permitió que se produjese potencia y se mantuviese una velocidad próxima a la constante en la cinta.
El estudio consistió en 3 sesiones. Durante la primera sesión de familiarización, cada atleta caminó y corrió de 2 a 3 min en la cinta en 4 inclinaciones (9.4, 30.0, 35.0 y 39.2). Durante la segunda y tercera, los sujetos aleatoriamente caminaron (ej., día 2) y corrieron (ej., día 3) durante 5 min en siete inclinaciones diferentes (9.4, 15.8, 20.4, 24.8, 30.0, 35.0, y 39.2°) correspondientes a velocidades en cinta (2.14, 1.29, 1.00, 0.83, 0.70, 0.61, y 0.55 m/s). Los sujetos tuvieron 5 min de descanso entre intervalos. La mitad de los sujetos caminaron en el día 2 y corrieron en el 3; la otra mitad hizo lo contrario. Estas inclinaciones y las combinaciones de velocidad se fijaron en una velocidad vertical de 0.35 m/s. Elegimos esta velocidad vertical sabiendo que en los records de los VK para hombres (29 min 42 s = 0.56 m/s velocidad vertical) y mujeres (34 min 44 s = 0.48 m/s velocidad vertical) y reconociendo la necesidad de intensidades submáximas para poder registrar ratios metabólicos en estados estables. El test piloto indicó que una velocidad vertical más rápida se obtendría a través de un metabolismo no oxidativo. Para cada sujeto, aleatorizamos las inclinaciones usadas tanto en el día 2 como en el 3.
Datos metabólicos. Para determinar los ratios metabólicos durante corriendo y caminando, usamos un sistema de análisis de gases espiratorios (TrueOne 2400; ParvoMedic, Sandy, UT). Los sujetos llevaban una mascarilla permitiéndonos recopilar el aire espirado y determinar el rato de oxígeno consumido (VO2) y la producción de dióxido de carbono (VCO2). Promediamos los datos de los 2 últimos minutos de cada intervalo. Después calculamos el ratio metabólico en W/kg usando la ecuación de Borckway (2). Solo incluimos los intervalos con ratios de intercambio respiratorio (RER) <1.0. Calculamos el coste vertical (J·kg-1·m-1) de caminar (Cwvert) y correr (Crvert) dividiendo la potencia metabólica total entre la velocidad vertical.
Parámetros biomecánicos. Para medir los parámetros de la zancada, grabamos cada intervalo usando una videocámara de alta velocidad (Casio EX-FH20) a 210 fps. Extrajimos los tiempos de contacto y de zancada durante 10 zancadas usando Kinovea 0.8.15 software (www.kinovea.org) y calculamos la frecuencia de zancada (=1/tiempo de zancada) y la longitud de zancada (=velocidad/frecuencia de zancada). Para determinar el el duty factor (fracción de cada zancada que cada pie está en contacto con el suelo), dividimos el tiempo de contacto de una pierna entre el tiempo total de zancada.
Análisis estadístico. Analizamos los datos usando el SPSS con el índice de significancia de P£0.05. Analizamos el coste vertical de caminar (Cwvert), el coste vertical de correr (Crvert), y parámetros biomecánicos con un modelo lineal general de medidas repetidas considerando dos factores (pendiente y tipo de paso: caminar vs correr). Continuamos el Bonferroni post hoc test cuando diferencias significativas eran detectadas. A 9.4º la velocidad en cinta era más rápida que la velocidad de transición corriendo-caminando, así que solo 9 sujetos fueron capaces de completar los 5 min del intervalo enteros usando un paso de caminar. Por ello, haciendo la comparación estadística en los intervalos de 9.4º, calculamos las variables para solo esos 9 sujetos.
RESULTADOS
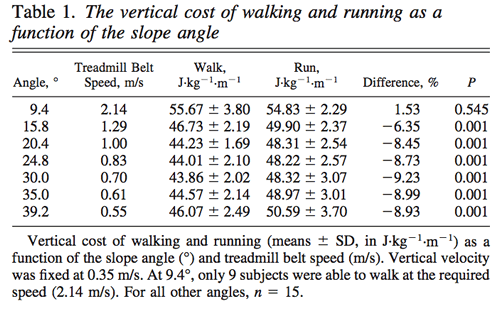
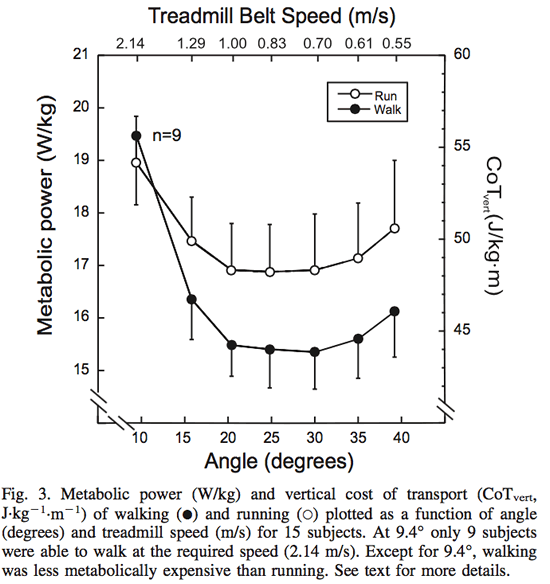
Coste vertical de caminar y correr. A 9.4°, el coste vertical de caminar (Cwvert) fue numéricamente un poco mayor que el coste vertical de correr (Crvert) pero sin diferencias significativas (n = 9; +1.54%; P = 0.545). Sin embargo, Cwvert fue significativamente menor que Crvert a 15.8° (-6.35%; P = 0.001), 20.4° (-8.45%; P = 0.001), 24.8° (-8.73%; P = 0.001), 30.0° (-9.23%; P = 0.001), 35.0° (-8.99%; P = 0.001), and 39.2° (-8.93%; P = 0.001; Tabla 1).
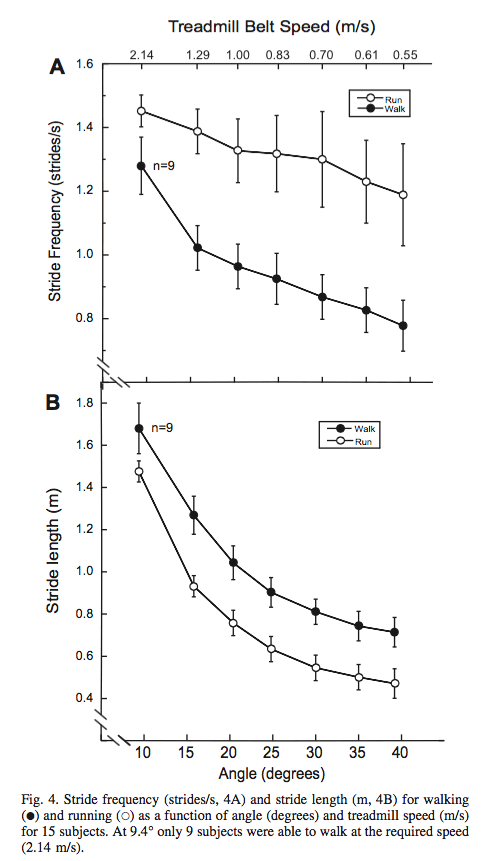
Cwvert fue numéricamente el más bajo a 30º (43.86±2.02 J·kg-1·m-1) pero no estadísticamente diferente de 20.4º (44.23±1.69 J·kg-1·m-1), 24.8° (44.10±2.10 J·kg-1·m-1), o 35.0° (44.57±2.14 J·kg-1·m-1) (Tabla 1 y Fig. 4). Cwvert a 15.8° fue menor que Cwvert a 9.4° (n = 9; -18.2%; P = 0.001). Además, Cwvert a 20.4°, 24.8, 30.0, y 35.0° fue menor Cwvert a 15.8° (media -5.47%; P = 0.001). Además, Cwvert a 39.2° significativamente más elevado que Cwvert a 20.4, 24.8, 30.0, and 35.0° (media +4.31%; P<0.001).
Crvert fue numéricamente más bajo a 24.8 (48.22±2.57 J·kg-1·m-1) pero no fue estadísticamente diferente de a 20.4° (48.31 ± 2.54 J·kg-1·m-1), 30.0° (48.32 ± 3.07 J·kg-1·m-1), o 35.0° (48.97 ± 3.01 J·kg-1·m-1; Tabla 1 y Fig. 3). Crvert a 15.8° fue menor que Crvert a 9.4° (-7.88%; P = 0.001). Como pasó caminado, Crvert a 20.4, 24.8, 30.0, y 35.0° fue menor Crvert a 15.8° (media -2.90%; P = 0.001). Finalmente, Crvert a 39.2° fue más elevado que Crvert a 20.4, 24.8, 30.0, y 35.0° (media -4.42%; P = 0.001).
Parámetros biomecánicos. La frecuencia de zancada caminando fue más baja que corriendo en todas la inclinaciones (media - 27.99% ±7.75%; P = 0.001; Fig. 4A). Por consiguiente, la longitud de zancada caminando fue mayor que corriendo en todas las inclinaciones (Fig. 4B). Tanto corriendo como caminando, la frecuencia y longitud de zancada decreció a medida que se aumentaba la inclinación correspondiendo a velocidades más bajas (Fig. 4, A and B). Duty factor fue >50% tanto para correr como para caminar en todas las combinaciones de velocidades/inclinaciones testadas, no indicando fase aérea. El duty factor caminando fue mayor que corriendo en todas las inclinaciones (media 10.29 ± 5.92%; P = 0.001) excepto a 40°.
DISCUSIÓN
Nuestros mayores hallazgos son 1) a lo largo de las inclinaciones y velocidades testadas en las que fijamos la velocidad vertical, caminar es más eficiente que correr, 2) hay un amplio rango de inclinaciones para los que el coste vertical de caminar y correr son minimizados, y 3) en las combinaciones de inclinación/velocidad que hemos estudiado, tanto en correr como en caminar, al menos un pie siempre está en contacto con el suelo.
Nuestros resultados apoyan la hipótesis que una velocidad vertical fija de 0.35 m/s, caminar podría ser más eficiente que correr en pendiente empinadas, aunque a 9.4° no hubo diferencias significativas entre correr y caminar. La explicación entre la diferencia energética entre caminar y correr no está clara. Sabemos que el péndulo invertido y el efecto “muelle” que conserva la energía mientras caminamos y corremos, respectivamente, están deshabilitados en la locomoción con pendiente ascendente (8, 24) pero no es todavía posible cuantificar esos efectos, Minetti et al. (18) mostraron que durante la locomoción en ascenso el “trabajo interno” que le corresponden a las extremidades son en realidad mayores caminando que corriendo, a pesar de las frecuencias de zancada más bajas caminando. Kram y Taylor (13) establecieron que el ratio metabólico es inversamente proporcional al tiempo de contacto durante la carrera. A las inclinaciones y velocidades estudiadas en el presente estudio, el tiempo de contacto para correr fue de promedio 34.4±3.2% menor que caminando y esto podría explicar, al menos parcialmente, el coste metabólico diferentes entre caminar y correr. Además, a causa de cómo las piernas están posicionadas de manera diferente en los dos tipos de paso, las ventajas mecánicas de los músculos extensores de la pierna son mayores caminando que corriendo (1). Fuerzas musculares menores requieren una activación de menor volumen muscular que es energéticamente más económico, sin embargo, no somos conocedores de ninguna medida mecánica ventajosa para la locomoción en pendiente ascendente.
A 9.4°, la velocidad en cinta (2.14 m/s) fue mucho más rápida que durante los otros intervalos y próxima a la carrera de transición espontánea a en llano (»2m/s) (3, 11, 15).
En estudios anteriores (4, 10, 11) se ha demostrado que aquella velocidad de transición preferida es más baja en inclinaciones moderadas y que los humanos generalmente eligen el paso que minimiza su coste metabólico (17). En el presente estudio, a 9,4º y 2.14 m/s, todos los sujetos expresaron de manera informal que habría preferido correr. A 15.8° y 1.29 m/s, caminar fue significativamente más económico pero la mayoría de los sujetos expresaron que habrían preferido correr. Entre 20.4° y 1.00 m/s y 30.0° y 0.70 m/s los sujetos mencionaron que caminando se sintieron más cómodos. Sin embargo, sin restricciones, ellos creyeron que habrían preferido alternar correr y caminar cada 1 o 2 minutos. A 35.0° y 0.61 m/s y 39.2° y sólo 0.55 m/s, las preferencias en el paso fueron ambiguas. Los sujetos expresaron que ellos no prefirieron caminar (el paso más económico) porque sintieron que la carrera involucraba menos estrés músculo-esquelético y también el equilibrio era más exigente cuando caminaban.
Un futuro estudio centrado en el paso preferido, en el coste metabólico y la percepción de esfuerzo durante caminar y correr en distintas inclinaciones son necesarias para entender mejor este aspecto.
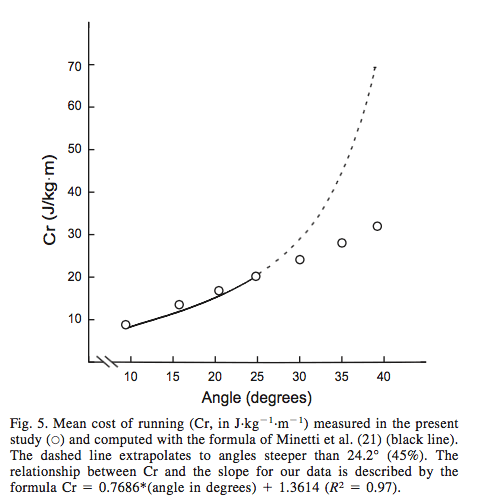
Nosotros rechazamos la segunda hipótesis. Más allá de haber distintas recomendaciones óptimas, encontramos que hay un rango de inclinaciones para que Cwvert y Crvert sean minimizados. Tanto para caminar como para correr, el valor mínimo evaluado fue 20.4 y 35.0º. Una segunda regresión polinómica sugiere que el valor mínimo para Cwvert y Crvert fue alcanzado a 28.4 (R2 = 0.64) y 27.0 (R2 = 0.33), respectivamente. A inclinaciones menores a 20º, Cwvert y Crvert son significativamente mayores. Esto se podría prever en parte por la mayor potencia metabólica requerida por soportar el peso corporal en la cinta de correr a velocidades más rápidas (9). Además, en la inclinación más alta que hemos visto, en 39.2º, hubo un incremento en Cwvert y Crvert, que creemos que es causado por la dificultad de mantener el equilibrio en este tipo de inclinaciones. Parte del estímulo del equilibrio fue debido por el hecho de que a 39.2º, la la velocidad en la cinta era de sólo 9.55 m/s y requería de tiempos de contacto exagerados (0.924 ± 0.09 s para caminar y 0.588 ± 0.11 s para correr). En un estudio piloto, dos sujetos intentaron caminar y correr con una inclinación en cinta de 45º y Cwvert y Crvert se incrementaron drásticamente comparado con »40º. El equilibrio fue bastante más difícil para los sujetos de ese estudio piloto y frecuentemente se agarraron al pasamanos. Además, en esa fuerte inclinación, los dos sujetos manifestaron incomodidad en sus pantorrillas y pies. Por esta razón, “sólo” estudiamos hasta 39.2º en este experimento. Para Cw y Cr en ángulos entre 10 y 24.8º, nuestros resultados son congruentes con la quinta fórmula de regresión polinómica dada por Minneti et al. (21). Sin embargo, extrapolar más allá de 24.8º esta fórmula provocaría grandes sobrestimaciones de la Cw y Cr (Fig. 5).
En un reciente estudio desde nuestro laboratorio, Hoogkamer et al. (9), propusieron una nueva explicación para el coste metabólico de correr en pendiente ascendente relativamente poco empinada <9º. En ese modelo, el coste de correr (Cr) es determinado por tres factores: el coste de salto perpendicular, el coste paralelo de frenado y el coste de elevación del centro de masas. Ellos asumieron una constante eficiencia de rendimiento en el trabajo de elevación del centro de masas, sus resultados apoyaban esa asunción, y ellos derivaron un valor de »29% de eficiencia. En el presente estudio, el ratio de trabajo vertical fue constante entre las diferentes inclinaciones y así, con la misma eficiencia, el coste vertical sería el mismo entre las condiciones de carrera. En el estudio de Hoogkamer et al., ya que la inclinación era aproximadamente de 9º, el coste de de frenado paralelo y la propulsión (la “propulsión malgastada”) presumiblemente es nula. Finalmente, Hoogkamer et al. concluyeron que el coste de salto perpendicular no cambiaría en las pendientes moderadas que ellos estudiaron. En pendientes más pronunciadas presentadas en este estudio, sólo basándonos en la trigonometría, las fuerza perpendiculares serían menores que durante la carrera en llano (ej., »13% reducida en 30° de inclinación, coseno = 0.866). No obstante, las velocidades de carrera en las inclinaciones estudiadas aquí fueron mucho más bajas que las velocidades de carrera en llano y con mayores tiempos de contacto. Un mayor tiempo de contacto presumiblemente permitiría el reclutamiento de fibras musculares lentas (más económicas) para generar fuerzas perpendiculares, pero un tiempo de contacto más largo empeora el efecto muelle (retorno elástico) y por ello sería menos económico (5). En general, desde la perspectiva de Hoogkamer et al. (9), la amplia meseta observada de Crvert para los ángulos de 20.4 a 35.0 corriendo, probablemente resultarían de contrarrestar el almacenamiento elástico versus los costes para el movimiento perpendicular a diferentes velocidades y combinaciones de inclinaciones. Un modelo similar para pendientes de subida caminando todavía no ha sido propuesto.
Tal y como hipotetizamos, no había una fase aérea corriendo cuesta arriba, ej., el duty factor (media 62.7 ± 0.80%) fue > 50% en todas las inclinaciones evaluadas. Esto sugiere que otros parámetros deberían ser considerados para diferenciar entre caminar y correr cuesta arriba. McMahon et al. (16) definieron como “Groucho running” al paso sin fase aérea que todavía implicaba un movimiento vertical del centro de masas, ej., el centro de masas fue más bajo en la fase media del apoyo. Rubenson et al. (23) usaron el término “grounded running” para el mismo fenómeno en pájaros (avestruces). A causa de que nuestros sujetos estaban corriendo cuesta arriba, la descripción del centro de masas probablemente no se aplique (8). Sin embargo, cuando preguntamos a nuestros sujetos si “caminar” o “correr”, todos inmediatamente e intuitivamente distinguieron los dos tipos de paso. Estudios previos reportaron que cuando la velocidad en cinta es fija, en inclinaciones más empinadas, la longitud de zancada y el tiempo en fase aérea decrece y la frecuencia de zancada aumenta (7, 22). Nosotros observamos un descenso en la frecuencia y la longitud de zancada en inclinaciones elevadas (Figs. 4 and 5) porque la velocidad de la cinta fue más baja en las inclinaciones mayores que evaluamos. Así, con este diseño experimental, podríamos determinar como la velocidad y la inclinación afectan independientemente a la frecuencia y longitud de zancada.
Limitaciones y futuro estudio. Una limitación de nuestro estudio es que fue realizado en cinta mientras que las carreras de VK son realizadas en terreno irregular (cuestas, sendas…) con la presencia de piedras, escalones, grava... Voloshina y Ferris (26) reportaron que el gasto energético de correr en un terreno irregular en cinta fue solo un 5% más alto que en en terreno regular en una cinta. No obstante, Zamparo et al. (27) mostraron que correr en un terreno arenoso requiere un 20% más de energía que hacerlo en terreno firme.
Así, el coste energético durante una carrera de VK real es seguramente algo más alto que el que nosotros medimos en la cinta. Otra limitación fue que nuestra cinta no permitió el uso de palos. En el record mundial de VK así como en la mayoría de marcas más rápidas outdoor se hicieron utilizando palos.
Futuros estudios deberían comparar los ascensos caminando y corriendo sin palos para determinar si el uso de palos es una ventaja. Más estudios que involucren diferentes combinaciones de velocidad vertical, velocidades en cinta e inclinaciones son también necesarios. Finalmente, una comparación biomecánica más rigurosa de caminar versus correr es requerida ya que las las características que se definen en estas inclinaciones y corriendo y caminando no están claras.
En conclusión, hemos estudiamos el gasto de caminar y correr en inclinaciones sustancialmente mayores que cualquier estudio previo. Encontramos que tanto para caminar como para correr hay un rango de inclinaciones (20.4-35.0°) para las cuales el gasto de energía es minimizado. Nuestros datos sugieren que, para conseguir los mejores resultados, las carreras de VK deberían ser realizadas dentro de este rango de inclinaciones. Y aunque otros factores deberían ser importantes, en inclinaciones pronunciadas, los atletas pueden reducir el gasto de energía caminando en vez de corriendo.
Referencias
1. Biewener AA, Farley CT, Roberts TJ, Temaner M. (2004). Muscle mechanical advantage of human walking and running: implications for energy cost. J Appl Physiol 97: 2266–2274
2. Brockway JM. Derivation of formulae used to calculate energy expen- diture in man. (1987). Hum Nutr Clin Nutr 41: 463–471.
3. di Prampero PE. (1986). The energy cost of human locomotion on land and in water. Int J Sports Med 7: 55–72.
4. Diedrich FJ, Warren WH. (1998). The dynamics of gait transitions: effects of grade and load. J Mot Behav 30: 60–78
5. Farley CT, Blickhan R, Saito J, Taylor CR. (1991). Hopping frequency in humans: a test of how springs set stride frequency in bouncing gaits. J Appl Physiol 71: 2127–2132
6. Farley CT, Ferris DP. (1998). Biomechanics of walking and running: center of mass movements to muscle action. Exerc Sport Sci Rev 26: 253–285
7. Gottschall JS, Kram R. (2005). Ground reaction forces during downhill and uphill running. J Biomech 38: 445–452
8. Gottschall JS, Kram R. (2006). Mechanical energy fluctuations during hill walking: the effects of slope on inverted pendulum exchange. J Exp Biol 209: 4895–4900
9. Hoogkamer W, Taboga P, Kram R. (2014). Applying the cost of generating force hypothesis to uphill running. PeerJ 2: e482.
10. Hreljac A. (1995). Determinants of the gait transition speed during human locomotion: kinematic factors. J Biomech 28: 669–677
11. Hreljac A, Imamura R, Escamilla RF, Edwards WB. (2007). Effects of changing protocol, grade, and direction on the preferred gait transition speed during human locomotion. Gait Posture 25: 419–424
12. Kay A. (2012). Pace and critical gradient for hill runners: an analysis of race records. J Quant Analysis Sports 8: 1–17
13. Kram R, Taylor CR. (1990). Energetics of running: a new perspective. Nature 346: 265–267
14. Margaria R. (1938). Sulla fisiologia e specialmente sul consumo energetico della marcia e della corsa a varia velocita ed inclinazione del terreno. Atti Accademia Nazionale dei Lincei 7: 299–368
15. Margaria R, Cerretelli P, Aghemo P, Sassi G. (1963). Energy cost of running. J Appl Physiol 18: 367–370
16. McMahon TA, Valiant G, Frederick EC. (1987). Groucho running. J Appl Physiol 62: 2326 –2337
17. Mercier J, Le Gallais D, Durand M, Goudal C, Micallef JP, Prefaut C. (1994). Energy expenditure and cardiorespiratory responses at the transition between walking and running. Eur J Appl Physiol Occup Physiol 69: 525–529
18. Minetti AE, Ardigo LP, Saibene F. (1994). Mechanical determinants of the minimum energy cost of gradient running in humans. J Exp Biol 195: 211–225
19. Minetti AE, Ardigo LP, Saibene F. (1994). he transition between walking and running in humans: metabolic and mechanical aspects at different gradi- ents. Acta Physiol Scand 150: 315–323.
20. Minetti AE, Cazzola D, Seminati E, Giacometti M, Roi GS. (2011). Skyscraper running: physiological and biomechanical profile of a novel sport activity. Scand J Med Sci Sports 21: 293–301
21. Minetti AE, Moia C, Roi GS, Susta D, Ferretti G. (2002). Energy cost of walking and running at extreme uphill and downhill slopes. J Appl Physiol 93: 1039 –1046
22. Padulo J, Annino G, Migliaccio GM, D’Ottavio S, Tihanyi J. (2012). Kine- matics of running at different slopes and speeds. J Strength Cond Res 26: 1331–1339
23. Rubenson J, Heliams DB, Lloyd DG, Fournier PA. (2004). Gait selection in the ostrich: mechanical and metabolic characteristics of walking and running with and without an aerial phase. Proc Biol Sci 271: 1091–1099
24. Snyder KL, Kram R, Gottschall JS. (2012). The role of elastic energy storage and recovery in downhill and uphill running. J Exp Biol 215: 2283–2287
25. Thorstensson A, Roberthson H. (1987). Adaptations to changing speed in human locomotion: speed of transition between walking and running. Acta Physiol Scand 131: 211–21.
26. Voloshina AS, Ferris DP. (2015). Biomechanics and energetics of running on uneven terrain. J Exp Biol 218: 711–719,.
27. Zamparo P, Perini R, Orizio C, Sacher M, Ferretti G. (1992). The energy cost of walking or running on sand. Eur J Appl Physiol Occup Physiol 65: 183–187