Fraccionamiento de la Masa Corporal: Un Nuevo Método para Utilizar en Nutrición, Clínica y Medicina Deportiva

Los autores abogan por el abandono de los índices, los métodos densitométricos convencionales y otros métodos basados en suposiciones de constancia biológica de las masas tisulares, a favor del escalado normativo global del Sistema de Escala O (O-Scale SYSTEM) o de un fraccionamiento antropométrico de la masa corporal en cinco componentes estructurales: piel, tejido adiposo, músculo, hueso y tejido residual. La justificación del nuevo método de fraccionamiento parte de un individuo unisexuado de referencia (escala Phantom) para cada una de las variables indicativas, y se valida de acuerdo a: 1) capacidad de la suma de las fracciones estimadas para determinar la masa corporal total en 1l subgrupos distintos de individuos de ambos sexos (n = 1,669); y 2) su capacidad para predecir valores medios de masas fraccionales, obtenidas por disección, y determinación del peso corporal total en 25 cadáveres humanos de ambos sexos. Se adjuntan también apéndices para la definición precisa de las masas fraccionales estimadas y las ecuaciones utilizadas por el método.

INTRODUCCION

En 1974, cien años después de la muerte de Adolph Quetelet, considerado como el primer cinantropometrista, apareció el primer ordenador personal. El Altair 8800 era un kit que debía montar uno mismo. Tenía 256 bytes, no Kilobytes, de memoria y no tenía teclado ni monitor. Había que programarlo con interruptores y palancas y leer los resultados por medio de luces apagadas o encendidas de una tabla binaria.

En aquella época, se utilizaban, por su sencillez de cálculo, métodos de determinación de la composición corporal a base de índices o fórmulas sencillas de predicción de la cantidad de grasa por el espesor del pliegue cutáneo. Los índices, como el Índice de Masa Corporal (IMC o Body Mass Index - BMI), no son ni tan útiles ni tan informativos como parece. De hecho, hemos demostrado que cuando se aplica a amplias muestras de hombres y mujeres, de edades comprendidas entre los 20 y 70 años, el IMC tiene solamente una eficiencia del 15% en la predicción de la suma de cinco espesores de pliegue cutáneo, y ligeramente mejor en la predicción de la suma de espesores de pliegue cutáneo corregidos (Ross et al. 1988).

En otros trabajos hemos puesto a prueba las suposiciones densitométricas del modelo bicompartamental de estimación de los compartimentos graso y no graso (Ross et al., 1984; Martin et al. 1984; Martin et al. 1986 b; Ross et al. 1987).

El modelo bicompartamental de composición corporal, llamado "la regla de oro" (gold standard) por Wilmore (1983) y que se basa en la suposición de una ;densidad constante para cada uno de los compartimentos, es de una simplicidad elemental. Como se muestra en la Figura 1, si al 100% de grasa se le asigna una densidad de 0,90 g/ml, y a lo no graso (magro restante) una densidad de 1,10 g/ml, conociendo la densidad corporal total obtenida por peso subacuático (peso corregido, teniendo en cuenta el volumen residual atrapado en los pulmones), se puede predecir el % de tejido adiposo de la manera indicada.

La suposición de que la grasa (lípido extractable con éter) tiene una densidad constante de 0,90 g/ml se refiere solamente a los triglicéridos y no tiene en cuenta los fosfolípidos ni el colesterol del sistema nervioso, que presentan una densidad superior. Incluso, dando por cierta la suposición de una densidad constante de un compartimiento graso anormalmente definido, continua siendo falso de que el compartimiento magro, en humanos, tenga una densidad constante de l , 10 g/ml o un valor similar. Martin et al. (1986), prueban la inconstancia de la masa libre de tejido adiposo diseccionable, demostrando, en cadáveres, que el tejido óseo, muscular y la masa residual no están presentes en proporciones fijas y que las densidades de cada uno de estos tejidos no es constante, especialmente la del hueso. Dichas observaciones son consistentes con las variaciones detectadas por técnicas médicas de visualización tales como la técnica de absorción doble de fotones (Maszes et al., 1984). Por otro lado, como indican Martin et al. (1986 a), además de la falta de validez de la suposición de densidades constantes para los dos compartimentos, deben aceptarse al menos, otras cinco suposiciones demostrablemente falsas para convertir las distancias lineales entre las placas de compresión del compás de pliegues, en lípidos extraíbles con éter (grasa): 1) una compresibilidad constante de la piel y el tejido adiposo, 2) un valor despreciable para las dos capas de piel, 3) una estructura fija de deposición del tejido adiposo, 4) una fracción constante de grasa en el tejido adiposo, y 5) una proporción fija de grasa interna y externa.

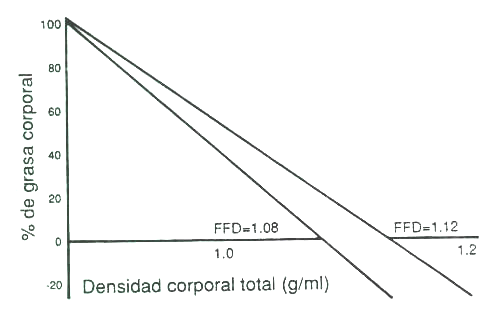
Figura 1. Densidad de masa magra. FFD = Fast Free Density

En ciencias, no se debe confundir nunca la calidad del trabajo o su validez, con el costo del equipo utilizado. Por falta de espacio no es posible aquí una revisión de los métodos más recientes de determinación de "grasa" o "masa corporal magra" por métodos bioquímicos, ultrasonidos, infrarrojos o aparatos basados en la bioimpedancia eléctrica. Debe remarcarse, sin embargo, que todos ellos requieren suposiciones, no comprobadas, de constancia biológica de algún tipo . El criterio de validez utilizado normalmente es el método bicompartamental de composición corporal... una argumentación sobre si misma, en el mejor de los casos.

Con el fácil acceso a los microordenadores, no hay razón, excepto la incapacidad de medir con precisión y exactitud, para apoyarse en métodos de composición corporal de antaño o en aparatos de "alta tecnología", con pretensiones de validez basadas en suposiciones de constancia biológica.

OPCION DE LA ESCALA O (O-Scale System)

Uno de los nuevos programas analíticos que no arrastra tales suposiciones es el Sistema Avanzado de Escala O de Determinaciones Físicas (Advanced 0Scale System on Physique Assesment) de Ward R. et al., (1989). Esencialmente se trata de un programa de ordenador normal, que proporciona: 1) índices standard de adiposidad (suma de seis pliegues cutáneos ajustada a la estatura) y peso proporcional (ajuste geométrico del peso corporal a la estatura); 2) una lista de valores para ocho pliegues cutáneos, diez perímetros, dos diámetros de hueso y cuatro pliegues cutáneos corregidos respecto a los percentiles 4, 50 y 96; 3) un perfil de proporcionalidad de 25 perímetros, altamente ajustado referente a hombres y mujeres tipo, definido para cada alto de edad entre los 6 y 19 altos, y a continuación, de cinco en cinco altos hasta la edad de 70. Basado en datos obtenidos de 25.000 canadienses, el Sistema de Escala O constituye una referencia estable para la determinación del estado morfológico y la monitorización de los cambios. Permite la comparación de los datos del paciente con los obtenidos en otras determinaciones anteriores, con la de cualquier otro sujeto o con los valores medios de cualquier grupo muestra.

OPCION DEL FRACCIONAMIENTO

Desde finales de los 70, hemos estado interesados en la evidencia publicada en el clásico artículo sobre fraccionamiento antropométrico de la masa corporal de Jindrich Matiegka (1921), citado en una publicación por Drinkwater y Ross (1980), en la tesis doctoral de D. Drinkwater (1984), y más recientemente en la tesis de grado de D. Kerr (1989).

La premisa básica en el modelo de Fraccionamiento de Kerres que los indicadores antropométricos de las masas tisulares partían de un humano unisexuado de referencia o Phantom así como también las masas fraccionales definidas.

VALIDEZ

La validez del método estaba basada en dos criterios: 1)la capacidad del método para predecir la masa corporal a partir de cinco estimaciones fraccionales de masas, en hombres y mujeres, viejos y jóvenes, en buen o mal estado físico, representando un amplio espectro de actividad física habitual; y 2) concordancia con las masas tisulares obtenidas por disección, bajo la dirección de J.P. Clarys de la Universidad Autónoma de Bruselas en una muestra de cadáveres de 12 hombres y 13 mujeres, tal como se describe en la tesis doctoral de A. Martin (1984) y D. Drinkwater (1984), de Simon Fraser University.

Ambos criterios fueron bastante bien satisfechos, tal como se muestra en las tablas resumidas de la comunicación de Kerr y Ross (1990). En la Tabla 1 se muestra que el modelo fue capaz de calcular las masas corporales totales obtenidas en l1 muestras, escogidas a fin de representar la variabilidad humana. Todas las correlaciones entre la masa predicha a partir de la suma de las cinco fracciones y la masa obtenida, sobrepasaban 0.93, excepto para remeros de peso ligero, en los que se halló una variancia reducida respecto a la media (de todos modos es de resaltar que la muestra de remeros tenían los errores standard del peso estimado más bajos).

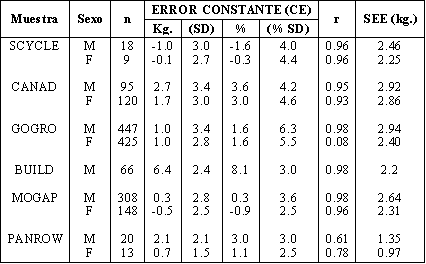
Tabla 1. Precisión en la predicción de valores medios del peso corporal por método de 5 componentes fraccionales, aplicados a 11 muestras "in vivo”.

Especificaciones: SCYCLE (Ciclistas senior de 49 a 77 años); CANAD (Estudiantes universitarios canadienses de 18 a 35 años); COGRO (Niños canadienses de 6 a 17 años); BUILD (Fisicoculturistas de nivel international); MOGAP (Deportistas de los Juegos Olímpicos de Montreal, 1976); PANROW (Remeros categoría livianos, Juegos Panamericanos de Indianápolis, 1987).

CE (error constante) = Diferencias de medias entre peso Obtenido y peso Predictivo (CE = P-O, en Kg.); en Kg. (absoluto) y en % (relativo), con sus respectivos desvíos standard;. r (coef. de correlación) = el coeficiente que expresa la correlación existente el peso obtenido de balanza y el peso predictivo calculado por el modelo fraccional.

SEE (Kg.) = Error de estimación standard

• SEE = SD. (1 – r²)^0.5, en donde SD es la desviación standard de la variable peso predictivo.

Como se muestra en la Tabla 1, cuando se aplica a la muestra de cadáveres, los estimados de masa fraccional derivados independientemente, fueron capaces de predecir los valores medios obtenidos, en forma bastante exacta, aunque no se alcanzaron niveles de predicción individual, como indica el coeficiente de correlación que va de 0,717 para la masa residual estimada, a 0,941 para la masa muscular estimada.

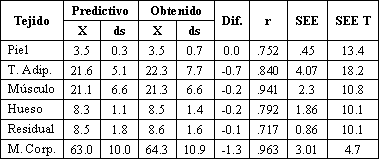
Tabla 2. Exactitud en la predicción de masas tisulares por disección de cadáveres de 12 hombres y 13 mujeres, por el uso del método antropométrico de 5 masas fraccionales.
Nota: Valores en Kg, excepto r y error standard de la estimación (SEE).

DISCUSION

Para poder afirmar una predicción individual, creemos que los coeficientes de correlación deberían sobrepasar 0,95 y el error de estimación standard debería ser menor del 5%. Algunos colegas entusiastas alegan que el modelo standard resulta irrazonable para la muestra de cadáveres y aluden a la elevada correlación con la masa muscular y a la habilidad del nuevo método de haber sido capaz de predecir las medias de masa fraccional de los cadáveres y justificar la masa corporal total (r = 0,963, SEE 4,7%).

Estudios en desarrollo conjunto con Simon Fraser University y la Universidad de Barcelona están enfocados a la optimización del modelo de proporcionalidad derivando la masa dérmica a partir de perímetros en lugar de hacerlo a partir de la superficie, modificando la estimación de la masa muscular a fin de reducir los efectos extremos de la displasia de la parte superior del cuerpo, estimando la adiposidad intema por medio de la utilización de perímetros protuberantes y usando el perímetro de los glúteos y del muslo como representación de la disposición regional de adiposidad.

Dado que el modelo fraccional en cinco masas esta basado en tejidos definidos anatómicamente, como se indica en el Apéndice A, puede ser definido nuevamente por medio de técnicas anatómicas cuantitativas avanzadas, tales como las técnicas de visualización de resonancia magnética. No se puede comparar directamente con los métodos de determinación de la composición corporal definida químicamente, ya que la "grasa" por definición química, con una densidad aproximada de 0.90 g/ml tiene aspecto de aceite de oliva y no es idéntica al tejido adiposo diseccionable definido anatómicamente, que se asemeja a la "grasa" que encontramos en la carne. Sin embargo, dado que el método de fraccionamiento anatómico comporta una antropometría no invasiva, podría convertirse en una técnica concomitante a todos los nuevos métodos, tal como el propuesto por Heymsfield et al. (1990), teniendo en cuenta, por supuesto, las distintas definiciones de las masas tisulares estimadas y las suposiciones de constancia biológica, así como los criterios de validación indirecta de estas últimas. A la hora de estimar anatómicamente las masas tisulares, desde luego, hay también suposiciones vulnerables, ya que los volúmenes derivados de la antropometría, para ser convertidos en masas, deben tener valores de densidad estimados, específicos para cada tejido, explícitos en el método de Drinkwater (1984) e implícitos en el método Phantom diseñado originariamente por Ross y Wilson (1974), tal como se utiliza en los algoritmos de Apéndice B para el fraccionamiento de Kerr, descriptor en este artículo.

SOLUCIONES DEL ORDENADOR

En el laboratorio de cineantropometría de Simon Fraser University se pide a los estudiantes que introduzcan medidas triples de un modelo global en el ordenador. El cálculo de las masas fraccionales, las suma de éstas y el porcentaje de error en la estimación de la masa corporal obtenida, es entonces un mero acoplamiento de operaciones. Actualmente, el programa para estudiantes está siendo analizado por colegas de la comunidad internacional. Se sabe que se realizara una versión comercial para uso científico y profesional.

APENDICE A: VARIABLES PARA LA DERIVACION DE MASAS FRACCIONALES

1. Masa de piel

• peso corporal
• estatura

2. Masa de tejido adiposo

• pliegue cutáneo triccipital
• pliegue cutáneo subescapular
• pliegue cutáneo supraspinal
• pliegue cutáneo abdominal
• pliegue cutáneo de la parte frontal del muslo
• pliegue cutáneo de la pantorrilla medial

3. Masa muscular

• perímetro del brazo relajado corregido por el pliegue cutáneo triccipital
• perímetro del antebrazo (no corregido)
• perímetro de la caja torácica, corregido por el pliegue cutáneo subescapular
• perímetro del muslo, corregido por el pliegue cutáneo de la parte frontal del muslo
• perímetro de la pantorrilla, corregido por el pliegue cutáneo de la pantorrilla medial

Fórmula General:

Perímetro corregido = Perímetro total - (π x Pliegue) / 10

4. Masa ósea

• diámetro biacromial
• diámetro biiliocristal
• diámetro biepicondilar del húmero
• diámetro bicondilar del fémur
• perímetro de la cabeza (la masa ósea del cráneo se predice independientemente)

5. Masa residual

• perímetro de la cintura, corregido por el pliegue cutáneo abdominal
• diámetro antero-posterior de la caja torácica
• diámetro transversal de la caja torácica

A la hora de construir el modelo a partir de muestras in vivo, la definición de los tejidos fue adaptada de la tesis de Martin (1984) y Drinkwater (1984).

Estas definiciones y el razonamiento para la selección de las variables arriba mencionadas, fue como se describe a continuación:

1. Piel: masa anatómicamente diseccionable de tejido conectivo, músculo liso, algo de músculo estriado superficial, pelo, glándulas, tejido adiposo asociado, nervios y vasos sanguíneos con sangre coagulada. La piel así definida, es considerada en función de la superficie corporal, el grosor y la densidad de la misma. Datos obtenidos de cadáveres muestran que la superficie de la piel disecada obtenida, es mayor en hombres que en mujeres, respecto a lo esperado, aplicando reglas geométricas teóricas. Se calcularon nuevas variables para las relaciones dimensionales de M0.425 y H0.725 en la fórmula de superficie de DuBois y DuBois (1916). El grosor de la piel fue estimado a partir de la relación de la masa de la piel obtenida respecto ala superficie de piel disecada, multiplicada por la densidad de piel obtenida. Esta fracción es la única que utiliza el peso corporal obtenido. Mantiene similitud geométrica, por ejemplo, con la suma de exponentes 0,425 + 3.(0,725) = 2 (que es la dimensión de un área). Se está estudiando un método alternativo para la derivación de la superficie basado en valores Z de Phantom.

2. Tejido adiposo: tejido separable por disección grosera y que incluye la mayor parte de tejido adiposo subcutáneo, el tejido adiposo omental que rodea a los órganos y las vísceras y una pequeña cantidad de tejido adiposo intramuscular. No es equivalente a la masa de grasa extraíble por éter químicamente, definida en el método densitométrico bicompartamental. En el modelo fraccional, el tejido adiposo fue basado en pliegues cutáneos de las extremidades y los lados del torso, reconociendo que las adiposidades de las extremidades predominan en las mujeres y las del torso en los hombres. Una subestimación sistemática en las mujeres y una sobreestimación sistemática en los hombres ha hecho pensar que en el uso de pliegues cutáneos y perímetros musculares corregidos puede ser de utilidad para predecir este tejido, si se optimiza la fórmula.

3. Músculo: todo el músculo esquelético del cuerpo, incluyendo tejido conectivo, ligamentos, nervios, versos sanguíneos y sangre coagulada y una cantidad indeterminada de tejido adiposo no separable físicamente del músculo. Excepto para el perímetro del antebrazo, el músculo fue estimado a partir de perímetros corregidos por el pliegue cutáneo (es decir, sustrayendo al perímetro, n x el grosor del pliegue cutáneo adyacente, en cm.). En el caso del perímetro del antebrazo no se hizo ninguna corrección porque en la mayoría de protocolos no se incluye la medida del pliegue cutáneo adyacente.

4. Hueso: tejido conectivo, incluyendo cartílago, periosteo y músculo que no hayan podido ser completamente eliminados por raspado; nervios, vasos sanguíneos con sangre coagulada y lípidos contenidos en la cavidad medular. Los diámetros biacromial y biiliocristal están incluidos, ya que son indicadores importantes del dimorfismo entre hombres y mujeres (Ross y Ward, 1982). Los diámetros del fémur y el húmero se duplican para que representen a las dos extremidades. Dado que los niños tienen una cabeza relativamente ancha, una escala por alturas de la medida de la cabeza se determinó independientemente al resto de la m asa del esqueleto, basándose en la escala Phantom de perímetros de cabeza (no corregida por la estatura).

5. Masa de tejido residual: órganos vitales y vísceras consistentes en tejido conectivo, nervios, vasos sanguíneos con sangre coagulada y tejido adiposo que no pudo ser físicamente diseccionado de los órganos del tracto gastrointestinal (excluyendo la lengua que se considera parte de la masa muscular de la cabeza), los órganos sexuales, remanente del mesenterio, el tracto bronquial, los pulmones, el corazón y los vasos mayores y todos los tejidos restantes y los fluidos no incluidos en las otras cuatro fracciones. La suposición básica es que la masa de tejido residual llena la cavidad del tórax y pelvis, en volumen. Ya que ésto es independiente de la longitud de extremidades, los valores Z de Phantom fueron relacionados a la talla sentado y no a la estatura.

APENDICE B: METODO ANTROPOMETRICO PARA EL FRACCIONAMIENTO DEL CUERPO EN PIEL, TEJIDO ADIPOSO, MUSCULO, HUESO Y TEJIDO RESIDUAL (D. KERR, 1988)

1. Predicción de la masa de piel

Para calcular la masa de piel,

M_S = SA • T_SK • 1,05

donde:

• MS = masa de piel en kg.
• SA = superficie en metros cuadrados
• 1,05 = densidad de la piel (dato obtenido de disección cadavérica)
• T_SK = grosor de la piel (dato obtenido de cadáveres): es 2,07 para los hombres y 1,96 para las mujeres

Para calcular la superficie corporal,

SA = C_SA • W^0.425 •, H^0.725 / 10.000

donde:

• W = masa corporal expresada como peso, en Kg
• H = estatura o altura en centímetros
• SA = superficie en metros cuadrados (m²)
• C_SA = 68,308 en hombres de edad; > 12 años
• 73,704 en mujeres de edad; > 12 años
• 70,691 en hombres y mujeres, < 12 años (representa la media de las constantes de hombres y mujeres)

Formula general para la predicción de masas de tejido adiposo, músculo, hueso y tejido residual (Táctica PHANTOM).

La táctica de fraccionamiento requiere derivar el índice de proporcionalidad Phantom para cada masa, objeto de acuerdo con la siguiente fórmula:

Z = 1/s • [V • (C_P /C_S )^d - P]

donde:

• Z = score de proporcionalidad Phantom
• V = valor de la/s variables
• d = constante dimensional: 1 para longitudes, diámetros y perímetros, 2 para áreas y 3 para volúmenes (como el peso)
• C_P = altura o talla Phantom
• C_S = altura o talla del evaluado
• P = valor Phantom para la variable V
• S = desviación estándar Phantom para la variable V

La suma de los valores antropométricos para cada subgrupo de variables predictivas , se utiliza para determinar una valor Phantom de proporcionalidad (Z) para cada masa de tejido: adiposo, músculo, hueso y residual. Se considera que la desviación del valor Phantom de proporcionalidad para cada masa de tejido, representa las características displásicas de la masa de tejido. Para calcular la masa fraccional para cada tejido, se utiliza la siguiente fórmula:

M = (Z • s + P) / (C_P / C_S)³

donde:

• M = cualquier masa, por ejemplo: masa adiposa, masa de tejido esquelético, masa muscular o masa residual (en Kg.)
• Z = valor de la proporcionalidad Phantom de cada masa (expresa la proporcionalidad Z del subgrupo de medidas asignado a una determinada masa de tejido)
• P = valor Phantom específico para la masa de tejido en cuestión
• S = desviación estándar Phantom para la masa de tejido que se calcula
• C_P = Altura o talla Phantom (para el cálculo de la masa residual se usa la altura o talla sentado)
• C_S= Altura o talla del evaluado
• 3 = exponente dimensional (asumiendo una similaridad geométrica donde masa = litros (o m³)

2. Predicción de la masa esquelética u ósea:

Ante todo debe aclararse que la masa esquelética u ósea, se calcula en forma separada: a) masa ósea de la cabeza; b) masa ósea del cuerpo.

La masa esquelética de la cabeza se predice de acuerdo con el método general antes descrito, así pues:

Z OSEA CABEZA = (perímetro de la cabeza – 56,0) / 1,44

Donde:

• 56,0 = perímetro Phantom de la cabeza
• 1,44 = desviación estándar Phantom para el perímetro de la cabeza
• M OSEA CABEZA = Masa ósea de la cabeza (en kg.)
• Z OSEA CABEZA = Score de proporcionalidad Phantom para masa ósea de la cabeza
• 1,20 = Constante del método para media de masa ósea Phantom de la cabeza (en kg.)
• 0,18 = Constante del método para desviación estándar de la masa ósea Phantom de la cabeza (en kg.)

La masa esquelética del cuerpo se calcula según las siguientes ecuaciones:

S OSEA CUERPO = sumatoria [ BIAC + BIIL + (2 • HUM) + (2 • FEM) ]

Donde:

• BIAC = diámetro biacromial
• BIIL = diámetro biiliocristal
• HUM = diámetro del húmero
• FEM = diámetro del fémur

Z OSEA CUERPO = [S OSEA CUERPO • (170,18 / HT) – 98,88] / 5,33

Donde:

• Z OSEA CUERPO = Score de proporcionalidad Phantom para masa ósea del cuerpo
• S OSEA CUERPO = Sumatoria antes descrita
• 98,88 = valor de sumatoria Phantom de los diámetros óseos
• 5,33 = valor de sumatoria Phantom de los desvíos estándar de los diámetros óseos
• 170,18 = Constante de altura Phantom
• HT = Altura o talla del evaluado

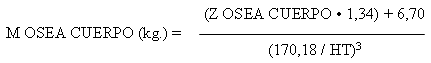
Donde:

• M OSEA CUERPO = masa ósea del cuerpo (en kg.)
• Z OSEA CUERPO = Score de proporcionalidad Phantom para masa ósea del cuerpo
• 6,70 = Constante del método para media de masa ósea corporal Phantom (en kg.)
• 1,34 = Constante del método para desvío estándar de masa ósea corporal Phantom (en kg.)

MASA TOTAL OSEA (en kg.) = M OSEA CUERPO + M OSEA CABEZA

3. Predicción de la masa adiposa

Se utilizan las siguientes ecuaciones:

S ADIP = sumatoria (TPSF + SSSF + SISF + ABSF + THSF + MCSF)

Z ADIP = [S ADIP • (170,18 / HT) – 116,41] / 34,79

Donde:

• 116,41 = sumatoria de medias Phantom de los pliegos cutáneos34,79 = sumatoria de los desvíos estándar Phantom para los pliegues cutáneos
• TPSF = pliegue cutáneo del tríceps
• SSSF = pliegue cutáneo subescapular
• SISF = pliegue cutáneo supraespinal
• ABSF = pliegue cutáneo abdominal
• THSF = pliegue cutáneo frontal del muslo
• MCSF = pliegue cutáneo de la pantorrilla media

M ADIP (kg.) = [ ( Z ADIP • 5,85) + 25,6] / (170,18 / HT)³

Donde:

• M ADIP = Masa adiposa (en kg.)
• Z ADIP = Score de proporcionalidad Phantom para la masa adiposa
• 25,6 = Constante del método para media de masa adiposa Phantom (en kg.)
• 5,85 = Constante del método para desvío estándar de la masa adiposa Phantom (en kg.)

4. Predicción de la masa muscular

S MUS = Sumatoria (P ARC + P FA + PTHC + P MCC + P CHC)

Z MUS = [S MUS • (170,18 / HT) – 207,21] / 13,74

Donde:

• 207,21 = sumatoria de las medias Phantom de los perímetros corregidos
• 13,74 = sumatoria de los desvíos estándar Phantom para los perímetros corregidos
• PARC = perímetro del brazo (relajado), corregido por el pliegue cutáneo del tríceps
• P FA = perímetro del antebrazo (no corregido)
• P THC = perímetro del muslo, corregido por el pliegue cutáneo del muslo frontal
• P MCC = perímetro de la pantorrilla, corregido por el pliegue cutáneo de la pantorrilla medial
• P CHC = perímetro de la caja torácica, corregido por el pliegue cutáneo subescapular

M MUS (kg.) = [ ( Z MUS • 5,4) + 24,5] / (170,18 / HT)³

Donde:

• M MUS = Masa muscular (en kg.)
• Z MUS = Score de proporcionalidad Phantom para masa muscular
• 24,5 = Constante del método para media de masa muscular Phantom (en kg.)
• 5,4 = Constante del método para desvío estándar Phantom para el músculo (en Kg.)

5. Predicción de la masa residual

S RES = Sumatoria (D APCH + D TRDH + P WC)

Donde:

• D APCH = Diámetro anteroposterior de la caja torácica
• D TRCH = Diámetro transversal de la caja torácica
• P WC = perímetro de la cintura, corregido por el pliegue cutáneo abdominal

Z RES = [S RES • (89,92 / SIT HT) – 109,35] / 7,08

Donde:

• S RES = Sumatoria de variables para el cálculo de la masa residual
• Z RES = Score de proporcionalidad Phantom para la masa residual
• 89,92 = altura o talla sentado Phantom
• 109,35 = Sumatoria de las medias Phantom de las variables usadas
• 7,08 = Sumatoria de los desvíos estándar Phantom de las mismas variables
• SIT HT = Altura o talla sentado

M RES ( en kg.) = [(Z RES • 1,24) + 6,10 ] / (89,92 / SIT HT)3

Donde:

• M RES = Masa residual (en kg.)
• Z RES = Score de proporcionalidad Phantom para masa residual
• 6,10 = Constante del método para la media de masa residual Phantom
• 1,24 = Constante del método para el desvío estándar para la masa residual Phantom

6. Predicción de la masa corporal total

La masa corporal predictiva se estima a partir de la suma de las cinco masas tisulares fraccionales calculadas:

M TOT ( en kg.) = ( M piel + M adiposa + M muscular + M ósea + M residual)

Donde:

• M TOT = masa corporal predictiva (en Kg.)

CONCLUSIONES

El modelo de calculo antropométrico de la composición corporal en 5 fracciones (piel, tejido adiposo, muscular, óseo y residual), se ha desarrollado a partir de los conceptos originales de Jindrich Matiegka (1921), continuado por D.T. Drinkwatcr, con su modelo de 4 componentes o fracciones y tiene una notable base de sustentación en la Táctica Phantom, propuesta por Ross y Wilson (1974), modificada posteriormente por Ross y Ward (1982).

Se ha dado evidencia de ser un sistema de cálculo independiente de las muestras (ya que se ha aplicado con éxito en diferentes tipo de muestras), es un método simple y poco costoso, utilizando protocolos de medición standard, validados por la Sociedad Internacional de Avances en Cineantropometría (I.S.A.K.).

Los Scores Z obtenidos son similares y comparables a los datos obtenidos de cualquier muestra, en la que se haya aplicado la escala Phantom.

El modelo, además, en su construcción revela su independencia de la muestra de cadáveres, mostrando una buena eficiencia en el cálculo de masas fraccionales de los mismos, especialmente en el cálculo de masa ósea y muscular; persisten algunos márgenes discretos de subestimación en mujeres y sobrestimación en varones, del tejido adiposo en la muestra cadavérica, hecho traspolable a la aplicación del modelo en seres vivos. De cualquier modo, el modelo de 5 componentes revela mejor performance en el cálculo de las masas de cadáveres y en el cálculo predictivo del peso corporal de 11 muestras "in vivo", que cualquier otro modelo fraccional anterior; especialmente por la heterogeneidad de las muestras (en sexo, edad, etnicidad y nivel de capacidad física y deportiva); ha silo demostrado que es el mejor método para cálculo de peso predictivo en niños y adolescentes.

Finalmente, como lo expresa la autora original, en el párrafo final de su tesis de grado, "el método de 5 masas fraccionales es considerado una parte del proceso de desarrollo de los modelos antropométricos de cálculo de composición corporal, y no una solución definitiva".