La Carrera en Cinta Rodante con Pendiente de 1% Refleja con Gran Precisión el Costo Energético de la Carrera al Aire Libre
Andrew M. Jones y Jonathan H. Doust
Chelsea School Research Centre, University of Brighton, Gaudick Road, Eastbourne BN20 7SP, UK
Artículo publicado en el journal PubliCE del año 2017.
Publicado 8 de septiembre de 2017
Resumen
Palabras clave: Evaluación de la aptitud física, economía de la carrera, carrera en cinta rodante
INTRODUCCIÓN
En los últimos años se ha incrementado el interés de los atletas y entrenadores por las pruebas fisiológicas que permitan monitorear los cambios en el estado de entrenamiento, predecir la capacidad de rendimiento real y que puedan ayudar a guiar la prescripción de los programas de entrenamiento. Esto ha centrado la atención en la validez de extrapolar la información obtenida en un ambiente de laboratorio hacia el ambiente exterior. Los corredores y jugadores de equipo, utilizan frecuentemente la cinta rodante para imponer el estrés del ejercicio; pero a diferencia de la carrera que se realiza al aire libre, durante la carrera en cinta rodante no hay resistencia al aire. Esto tiene consecuencias potenciales tanto para la termorregulación como para el costo energético asociado a poder superar la resistencia del aire. El movimiento del aire sobre el cuerpo ayuda a la pérdida de calor por convección y puede reducir la frecuencia cardiaca del ejercicio, porque disminuye la demanda de sangre periférica (Riggs et al., 1981; Williams y Kilgour, 1993). Para compensar esto, en el laboratorio se utilizan generalmente ventiladores eléctricos. El movimiento del aire de un ventilador ayuda a la pérdida de calor por convección, pero la masa de aire en movimiento es demasiado pequeña para imponer cualquier fuerza significativa que pueda retrasar el movimiento hacia delante. Para compensar la falta de resistencia al aire, algunos investigadores han utilizado ligeras inclinaciones en la cinta rodante entre las que se incluyen pendientes del 1,0% (Heck et al., 1985) y 2,0% (Tegtbur et al., 1993); sin embargo ninguno de estos estudios presentó datos en apoyo del ajuste elegido. Otros investigadores no han hecho ningún intento de explicar el efecto de la resistencia al aire (Noakes et al., 1990; Weltman et al., 1990) o no hicieron ninguna referencia a este tema (Hale et al., 1988).
El objetivo de este estudio fue determinar cual pendiente de la cinta rodante refleja con mayor exactitud el costo energético de la carrera al aire libre, en una gama de velocidades que se utilizan frecuentemente para entrenar y competir en un grupo de buenos corredores estándar. Planteamos la hipótesis que el consumo de oxígeno (VO2) de la carrera en el llano al aire libre en cualquier velocidad dada sería mayor que el VO2 de una carrera sin pendiente en cinta rodante ubicada en interior, y que la diferencia aumentará a medida que aumenta la velocidad.
MÉTODOS
Sujetos y diseños experimentales
En este estudio participaron voluntariamente nueve corredores varones que realizaban entrenamiento regular para carreras de fondo y que estaban completamente familiarizados con la cinta ergométrica y con los procedimientos de laboratorio. Los sujetos firmaron un formulario de consentimiento informado y el protocolo experimental fue aprobado por el comité de ética local. La edad media de los sujetos (SD), la masa corporal, la suma de cuatro pliegues cutáneos (Durnin y Womersley, 1974) y el VO2máx fueron 24,9±5,2 años, 72,0±3,3 kg, 24,9±5,7 mm y 65,1±2,7 ml kg -1 min-1 respectivamente.
Los sujetos debían correr durante 6 min en cada una de seis diferentes velocidades (2,92, 3,33, 3,75, 4,17, 4,58 y 5,0 m s-1, es decir, 10,5-18,0 km h-1) con una recuperación de 6 min entre las carreras. Esta rutina se repitió seis veces, cinco veces en una cinta rodante fijada en diferentes pendientes (0%, 0%, 1%, 2%, 3%) y una vez al aire libre. La condición de pendiente de la cinta rodante del 0% se aplicó dos veces para permitir la evaluación de la confiabilidad de la metodología utilizada en la prueba. Las pruebas se realizaron en seis días separados y las seis condiciones se aplicaron en orden aleatorio. Todos los sujetos realizaron las pruebas en 2 semanas. Las velocidades se seleccionaron de manera que representaran las velocidades típicas de entrenamiento y competición utilizadas por corredores varones competitivos pero no de élite.
En cada ocasión, los sujetos arribaron al laboratorio habiendo realizado un ayuno de toda la noche y cada sujeto fue evaluado a la misma hora del día (06.00-08.30 h). Se les prohibió realizar entrenamiento extenuante en las 24 horas previas a cada prueba. En cada ocasión los sujetos debían llevar el mismo calzado y equipo de correr liviano y realizaron la misma rutina individual de entrada en calor.
En los últimos 2 min de cada prueba, se determinó el VO2 mediante calorimetría indirecta. Los sujetos respiraron a través de una válvula Salford de baja resistencia con tubería Falconia de gran calibre. El aire expirado se recogió en bolsas de Douglas durante un período de 50 s. Se realizaron muestreos por duplicado para evaluar la repetitividad del método y también para establecer si se había alcanzado el estado estacionario. En el aire expirado se analizaron las concentraciones de O2 y CO2 con un transductor paramagnético (Servomex serie 1100, Crowborough, Inglaterra) o un transductor infrarrojo (Servomex modelo 1490) respectivamente, previamente calibrados utilizando estándares de tres puntos. El volumen de gas se determinó usando un medidor de gas seco (Harvard Ltd, Edenbridge, Inglaterra), previamente calibrado con un espirómetro Tissot y corroborado por contraprueba con una jeringa de gas de 7 litros de precisión (Hans Rudolph Inc., Kansas, EE.UU.). Todos los volúmenes de gas fueron corregidos para temperatura estándar y presión seca. La frecuencia cardiaca (FC) se midió por telemetría utilizando un monitor de frecuencia cardíaca Polar Sport Tester (Polar Electro, Kempele, Finlandia).
Procedimientos en la cinta rodante
Los sujetos corrieron sobre una cinta rodante modelo Woodway ELG2 (CardioKinetics, Salford, Inglaterra). En todos los sujetos se verificó la velocidad de la cinta rodante controlando las revoluciones de la correa de distribución durante el último minuto de cada carrera. La velocidad de la cinta rodante se ubicó siempre dentro de una diferencia de 0,03 m s-1 con respecto a la velocidad deseada. La pendiente de la cinta se controló con un nivel de burbuja y un teodolito colocado en una tabla de la madera larga. A través de un dispositivo de roscado, el nivel de burbuja podía ser ajustado con la horizontal exacta y la pendiente indicada por el teodolito.
Procedimientos efectuados al aire libre (outdoor),
Para la condición al aire libre los sujetos corrieron en un paseo marítimo llano (0,2 m de descenso en 1,6 km) con una vía de ida y otra de vuelta. El ritmo de las velocidades apropiadas fue marcado por un profesional que pedaleaba a un ritmo constante 2 m al lado del sujeto. La bicicleta fue equipada con una “computadora para bicicletas” para controla de manera continua la velocidad y la distancia recorrida. La computadora de la bicicleta se calibró regularmente usando la cinta rodante para asegurar la consistencia en las mediciones de velocidad entre las condiciones de laboratorio y de exterior. El tiempo total necesario para recorrer la distancia aportó una confirmación independiente de la velocidad media de carrera. En el análisis de datos se utilizaron las velocidades reales para cada individuo y los valores de las mismas tenían una diferencia que se encontraba dentro de los 0,06 m s-1 con respecto a la velocidad deseada. Poco después de alcanzar el punto de inflexión designado para cada carrera, se colocó a los participantes un clip de nariz y una boquilla. Transcurridos 60 s para permitir la habituación, se determinó el VO2 por el mismo método utilizado en las pruebas efectuadas en la cinta rodante. La bolsa de Douglas era sostenida por otro sujeto que corría aprox. 1 m al lado y ligeramente por detrás del sujeto. Este método aseguró una interferencia mínima con el movimiento de aire que experimentaba el sujeto. La velocidad del viento se midió de manera continua con un anemómetro. Las carreras al aire libre se realizaron cuando la velocidad del viento era inferior a 2,0 m s-1 Generalmente la velocidad del viento era mucho menor que este valor y fue en promedió 0,2-0,5 m s-1. Las temperaturas del laboratorio y de los exteriores fueron similares y oscilaron entre 14 y 18 °C.
Análisis estadístico
Los datos de repetitividad se analizaron con coeficientes de correlación producto-momento de Pearson y con el Test t para muestras apareadas. El VO2 y la frecuencia cardíaca (HR) en las diferentes velocidades y pendientes de carrera se analizaron con análisis de varianza con un nivel de significancia de P<0,05. Las diferencias significativas fueron analizadas mediante el test post-hoc de Tukey.
RESULTADOS
Alcance del estado estacionario
En este estudio era muy importante que las mediciones se realizaran en estado estacionario y que fueran confiables. El VO2 se midió dos veces durante los últimos 2 min de cada carrera. Las dos muestras presentaron una elevada correlación (r = 0,99). En todas las muestras (en todas las velocidades y pendientes tanto en el interior como en el exterior), el VO2 de la primera bolsa de Douglas (43,8-10,3 ml kg-1 min-1) no fue significativamente distinto al VO2 de la segunda bolsa Douglas (44,0-10,5 ml kg-1 min-1). En el análisis de datos se utilizó la media de las dos muestras. La confiabilidad test-retest se evaluó en la pendiente 0%. Los datos presentaron una elevada correlación (r = 0,99) y no se observaron diferencias significativas entre las dos pruebas. La frecuencia cardiaca (HR) durante la segunda prueba fue menor que la HR durante la primera prueba y la diferencia estadística fue casi significativa (P = 0,053). Sin embargo, la diferencia media en la FC entre la prueba y la contra prueba (1,6 lat/min) fue trivialmente pequeña.
Consumo de oxígeno
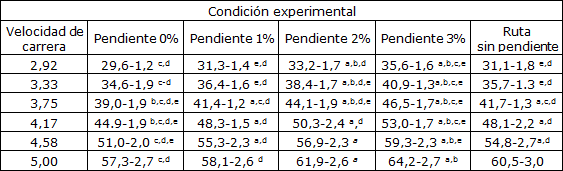
La Tabla 1 presenta los valores de consumo de oxígeno correspondientes a cada velocidad en ambas condiciones. El VO2 durante la carrera al aire libre no fue significativamente diferente del obtenido en cinta rodante con pendiente de 1% en ninguna de las velocidades utilizadas. La carrera al aire libre presentó una tendencia a ser similar a los valores obtenidos con pendientes de 0% o 1% en las velocidades más lentas, pero a velocidades más altas, el consumo de oxígeno de la carrera en ruta se acercó mas al consumo obtenido en la cinta rodante con pendiente de 1% y 2%. En la velocidad de 5,0 m s-1, el VO2 durante la carrera en ruta no fue significativamente diferente del VO2 obtenido en la cinta rodante con diferentes pendientes.
La relación entre VO2 y velocidad de carrera (v) fue altamente lineal. Las ecuaciones de regresión para las diferentes pendientes de la cinta rodante y para la carrera en ruta fueron las siguientes (VO2 en ml kg-1 min-1; v en m s-1):
Tabla 1. Consumo de oxígeno medio (ml kg-1 min-1) (-SD) en cada una de las velocidades utilizadas en cada condición experimental. Presenta diferencias significativas (P<0,05) con: a=pendiente 0%; b=pendiente 1%; c=pendiente 2%; d= pendiente 3%; e= ruta sin pendiente
La Figura 1 muestra la relación entre VO2 y velocidad para cada condición y líneas de regresión. La frecuencia cardíaca siguió un patrón de cambio similar al que presentó el consumo de oxígeno (Tabla 2). La carrera al aire libre en ruta llana provocó una frecuencia cardíaca ~ 3-4 latidos min-1 más alta que la que se observó durante la carrera en cinta rodante sin pendiente.
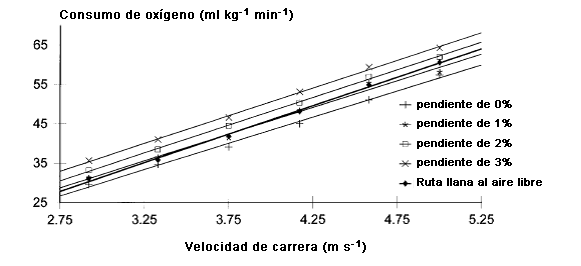
Figura 1. Relación entre el consumo de oxígeno y la velocidad de carrera en ruta llana al aire libre y en las diferentes condiciones de pendiente de la cinta rodante
Tabla 2. Frecuencia cardíaca media (lat min-1) (-S.D.) en cada velocidad (m s-1) y en cada condición experimental
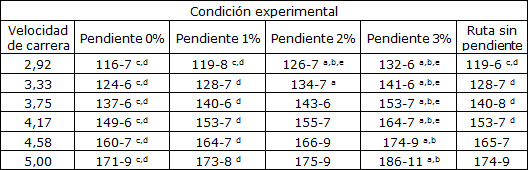
Presenta diferencias significativas (P<0,05) con: a=pendiente 0%; b=pendiente 1%; c=pendiente 2%; d= pendiente 3%; e= ruta sin pendiente
DISCUSION
Los resultados demuestran que el consumo de oxígeno de correr en una ruta llana al aire libre es mayor que cuando se corre en terreno llano en interior. Se observó que una pendiente de 1% en la cinta rodante reflejaba con mayor precisión el costo de oxígeno de correr al aire libre, y el costo de oxígeno en esta pendiente no fue significativamente diferente del costo de oxígeno de correr al aire libre para velocidades entre 2,92 y 5,0 m s-1. Estos resultados coinciden con lo observado por Davies (1980), quien, utilizando los datos obtenidos de un número limitado de sujetos que corrían en una cinta rodante alojada en un túnel de viento, concluyó que la resistencia del aire experimentada durante la carrera al aire libre en un día tranquilo equivalía a correr sobre una cinta con una pendiente de 1%. Los datos actuales también refuerzan el trabajo de Heck et al. (1985), en el cual se midió el lactato sanguíneo pero no el VO2 en cinta rodante con diferentes pendientes (0% -6%) y durante carrera al aire libre en diferentes superficies. Los autores concluyeron que era necesario que la pendiente de la cinta rodante se situara entre 0% y 2% para permitir la extrapolación de datos obtenidos en laboratorio a las condiciones de campo.
La evaluación precisa de la demanda de energía para ciertas velocidades de carrera requiere que el ejercicio se efectúe en estado estacionario. Barstow y Mole (1991) demostraron que en intensidades ubicadas por debajo del umbral de lactato se alcanza un estado estacionario de VO2 en menos de 3 min, pero en el caso de trabajo de intensidad moderada realizado por encima del umbral de lactato, la llegada al estado estacionario se demora. Un estado estacionario de VO2 nunca puede ser alcanzado durante el ejercicio de carga constante en intensidades mayores que aproximadamente 90% de VO2máx (Barstow y Mole, 1991). En los sujetos del presente estudio, el umbral de lactato (medido en un estudio paralelo por Jones y Doust, 1995) se situó entre 4,58 y 5,14 m s-1, por lo que algunos de los sujetos habrían estado realizando ejercicio por encima del umbral de lactato en la condición de 5 m s-1. Sin embargo, a pesar de la probabilidad de niveles elevados de lactato sanguíneo en algunos sujetos a 5,0 m s-1, las determinaciones de VO2 efectuadas por duplicado no fueron significativamente diferentes y todos los sujetos fueron capaces de completar los 6 min de carrera. En una minoría de sujetos en la carrera a 5 m s-1 y en pendientes superiores de 2% y 3%, el consumo de oxígeno se aproximó al VO2máx. Esto produjo un mayor error estándar del VO2 medio y esto explicaría probablemente la ausencia de diferencias significativas entre las condiciones que se observaron a 5 m s-1.
Aunque la relación VO2-velocidad para la carrera al aire libre es teóricamente curvilínea, con el VO2 aumentando como función cúbica de la velocidad (Pugh, 1970, 1971), Léger y Mercier (1984) informaron que, al menos para velocidades inferiores a 6,94 m s-1, la relación puede ser descripta adecuadamente mediante una función lineal. Sin embargo, curiosamente, su ecuación de regresión para la carrera al aire libre fue marcadamente diferente de la utilizada para describir la carrera en cinta rodante sin pendiente, particularmente para velocidades superiores a 4,17 m s-1. A pesar de la no linealidad entre el VO2 y la velocidad descrita por Pugh (1970) para la carrera en pista, Pugh también observó que la relación podría ser adecuadamente descrita por una función lineal entre 2,22 y 6,11 m s-1, una observación confirmada posteriormente por McMiken y Daniels (1976) y Davies (1981). En el presente estudio, la relación VO2-velocidad se ajustó casi perfectamente a una ecuación lineal (r2 = 99,7%), pero la función cuadrada y una función cúbica no se ajustaron tan precisamente (r2 = 98,3% y 95,7%, respectivamente). Debemos tener precaución con la extrapolación de los datos a velocidades superiores a 5,0 m s-1 ya que, tanto en los principios físicos como en los estudios empíricos sobre locomoción humana, la relación VO2-velocidad se torna mas curvilínea a velocidades más altas (McMiken y Daniels, 1976, Davies, 1980). Por ora parte, la tendencia de los datos, donde la pendiente de regresión para la condición de ruta presentaba una tendencia a superar la de cualquiera de las otras regresiones (ver Figura 1), sugiere que a velocidades de carrera de ~ 5-6 m s-1, una pendiente de 2% podría reflejar mejor el VO2 de la carrera en el llano al aire libre, mientras que a velocidades de alrededor de 2-3 m s-1, la pendiente de 0,5% sería la más apropiada. Aunque los sujetos de este estudio eran varones entrenados, no hay evidencia que sugiera que la relación velocidad-VO2 sea diferente entre varones y mujeres (Daniels y Daniels, 1992).
La ecuación de regresión para el VO2 sobre la velocidad durante la carrera en cinta rodante horizontal en el presente estudio fue similar a otros datos obtenidos en corredores entrenados (Costill et al., 1973, McMiken y Daniels, 1976, Bransford y Howley, 1977). Sin embargo, el VO2 a cualquier velocidad fue consistentemente más bajo (es decir, la economía de carrera era mayor) de lo que se ha informado anteriormente para sujetos no entrenados (Shephard, 1969, Bransford y Howley, 1977, Bassat et al, 1985, ACSM, 1991), y la ecuación de regresión para el presente estudio aportó estimaciones de VO2 que fueron considerablemente inferiores a las proporcionadas por la ecuación general calculada por Leger y Mercier (1984) a partir de datos agrupados de numerosos estudios iniciales. La evidencia de una mejor economía de carrera en sujetos entrenados es convincente (Daniels y Daniels, 1992, Morgan y Craib, 1992, Morgan et al., 1994). Sin embargo, incluso en los sujetos actuales, que tenían valores elevados y relativamente homogéneos de VO2máx (coeficiente de variación = 4%), se observaron grandes diferencias inter-individuales en la economía de carrera. Por ejemplo, el VO2 medido a 4,58 m m s-1 y 1% de pendiente varió de 49,3 a 57,0 ml kg-1 min-1. Estos resultados ponen de manifiesto el error potencial de estimar el VO2máx mediante pruebas de rendimiento como la lanzadera por tramos (Ramsbottom et al., 1988) y de la estimación del rendimiento solo a partir del VO2máx en grupos con VO2max relativamente similar (Morgan et al., 1989). Otros investigadores observaron grandes diferencias interindividuales en la economía de la carrera en grupos de corredores con VO2max homogéneos y demostraron que la economía de la carrera puede discriminar el rendimiento en tales grupos (Conley y Krahenbuhl, 1980, Powers et al, 1983).
Otras causas potenciales para explicar las diferencias entre las carreras en cinta rodante y carrera al aire libre incluyen que el corredor obtiene energía de las cintas rodantes motorizadas, cambios en el patrón de locomoción debidos a las diferentes superficies o la inestabilidad resultante de señales visuales que provienen de un entorno mas bien estático (Van Ingen Schenau, 1980), y el grado de familiarización con la carrera en cinta rodante (Conley y Krahenbuhl, 1980). Van Ingen Schenau (1980) cuestionó la existencia de alguna diferencia fundamental entre los dos tipos de carrera. El autor demostró matemáticamente que mientras la velocidad de la cinta de la máquina para correr sea constante, entonces es apropiado utilizar mecánicamente un sistema de coordenadas que se mueva con la correa. Con este sistema no existe ninguna diferencia mecánica significativa entre la carrera en cinta rodante y la carrera sobre el suelo. Aunque en algunas cintas rodantes la velocidad de la correa puede ser inestable, las modernas máquinas de alta velocidad diseñadas para el trabajo científico de precisión no sólo proporcionan un control estable de la velocidad, sino también una superficie estable que proporciona al corredor una retroalimentación proprioceptiva muy similar a la de la carrera en el suelo. Es posible que parte de la diferencia en el VO2 observado entre la carrera en cinta rodante y la carrera al aire libre sea consecuencia de las diferentes propiedades elásticas que existen entre las dos superficies de contacto. Dado que los sujetos llevaban los mismos zapatos de running en cada ocasión, se eliminó el 50% del efecto proveniente de la interacción con las superficies. El coeficiente de restitución (e) de la cinta rodante y de la ruta se determinó usando una pelota de basketball (para reflejar más cercanamente las características del caucho de las zapatillas para correr y de las cámaras de aire de las suelas). Las interacciones pelota-cinta rodante (e = 0.62) y pelota-ruta (e = 0.64) fueron similares y sugieren que los resultados de nuestro estudio no fueron afectados por las diferencias en las propiedades elásticas de las superficies. Para los atletas que están completamente acostumbrados a correr en cinta rodante, como los que participaron en el presente estudio, cualquier efecto sobre los costos de energía probablemente esté asociado con los efectos de la resistencia del aire. El hecho que nuestros datos presentaran un efecto proporcional a la velocidad de carrera apoya nuestra opinión de que el factor causal de la diferencia entre la carrera en interior y en exterior es el trabajo adicional necesario para atravesar el aire y no los efectos de factores mecánicos.
En conclusión, este estudio es el primero en demostrar que no existe diferencia significativa entre el VO2 medido en velocidades entre 2,92 y 5,0 m s-1 durante la carrera al aire libre y el VO2 medido a la misma velocidad a través de carrera indoor en cinta rodante con una pendiente de 1% durante 5 min. Esto indica que la extrapolación precisa de los datos generados mediante evaluación fisiológica de los corredores entrenados hacia condiciones de carrera en ruta al aire libre revela que la cinta rodante debe ser ajustada con una pendiente de 1%. La diferencia en el consumo de oxígeno entre la carrera al aire libre y la carrera en cinta rodante con pendiente igual a 0% es relativamente pequeña, aumentando de ~ 1,5 ml kg-1 min-1 en 2,92 m s-1 a ~ 3 ml kg-1 min-1 en 5,0 m s-1. Sin embargo, esta diferencia equivale a una diferencia entre la velocidad de carrera en cinta rodante y la velocidad de carrera al air libre de aproximadamente 0,07 m s-1 en la velocidad más lenta, aumentando a aproximadamente 0,28 m s-1 en la velocidad más alta. Expresado en términos de frecuencia cardíaca, la diferencia es de hasta 8 latidos min-1. Estas diferencias son de una magnitud significativa en la prescripción de programas de entrenamiento deportivo. El uso de pendientes adecuadas en la cinta rodante para compensar la falta de resistencia del aire en el laboratorio ayudará a mejorar la precisión con que se pueden utilizar las aplicaciones para el entrenamiento y las competencias al aire libre.
Agradecimientos
Agradecemos la ayuda de Robert Harley, David James y Danny Wood para la recolección de los datos.
Referencias
1. American College of Sports Medicine (1991). Guidelines for Graded Exercise Testing and Prescription. Philadelphia, PA: Lea and Febiger.
2. Barstow, T. and Mole, P. (1991). Linear and non-linear characteristics of oxygen uptake kinetics during heavy exercise. Journal of Applied Physiology, 71, 2099-2106.
3. Bassett, D., Giese, M., Nagle, F., Ward, A., Raab, D. and Balke, B. (1985). Aerobic requirements of overground ver-sus treadmill running. Medicine and Science in Sports and Exercise, 17, 477-481.
4. Bransford, D. and Howley, R. (1977). Oxygen cost of running in trained and untrained men and women. Medicine and Science in Sports and Exercise, 9, 41-44.
5. Conley, D. and Krahenbuhl, G. (1980). Running economy and distance running performance of highly trained athletes. Medicine and Science in Sports and Exercise, 12, 357-360.
6. Costill, D., Thomason, H. and Roberts, E. (1973). Fractional utilisation of the aerobic capacity during distance running. Medicine and Science in Sports and Exercise, 5, 248-252.
7. Daniels, J. and Daniels, N. (1992). Running economy of elite male and elite female runners. Medicine and Science in Sports and Exercise, 24, 483-489.
8. Daniels, J., Scardina, N., Hayes, J. and Foley, P. (1986). Elite and subelite female middle- and long-distance runners. In Sport Elite Performers (edited by D. Landers), pp. 57-72. Champaign, IL: Human Kinetics.
9. Davies, C.T.M. (1980). Effects of wind assistance and resistance on the forward motion of a runner. Journal of Applied Physiology, 48, 702-709.
10. Davies, C.T.M. (1981). Wind resistance and assistance in running. Medicine and Science in Sports and Exercise, 13, 199-213.
11. Durnin, J. and Womersley, J. (1974). Body fat assessed from total body density and its estimation from skinfold thick-ness: Measurements on 481 men and women aged from 16 to 72 years. British Journal of Nutrition, 32, 77-97.
12. Falls, D. and Humphreys, L. (1976). Energy cost of walking and running in young women. Medicine and Science in Sports and Exercise, 8, 9-13.
13. Hale, T., Armstrong, N., Hardman, A., Jakeman, P., Sharp, C. and Winter, E. (1988). Position Statement on the Physio-logical Assessment of the Elite Competitor. Leeds: British Association of Sports Sciences.
14. Heck, H., Mader, A., Hess, G., Mucke, S., Muller, R. and Hollman, W. (1985). Justication of the 4 mM lactate threshold. International Journal of Sports Medicine, 6, 117-130.
15. Jones, A.M. and Doust, J. (1995). The relationship of lactate minimum velocity to 8 km running performance and comparison with other methods of determining `aerobic threshold’. Journal of Sports Sciences, 13, 34.
16. Leger, L. and Mercier, D. (1984). Gross energy cost of hori¬zontal treadmill and track running. Sports Medicine, 1, 270-277.
17. McMiken, D. and Daniels, J. (1976). Aerobic requirements and maximal aerobic power in treadmill and track run-ning. Medicine and Science in Sports and Exercise, 8, 14-17.
18. Morgan, D. and Craib, M. (1992). Physiological aspects of running economy. Medicine and Science in Sports and Exercise, 24, 456-461.
19. Morgan, D., Baldini, F.D., Martin, P.E. and Kohrt, W.M. (1989). Ten kilometer performance and predicted velocity at VO2 max among well-trained male runners. Medicine and Science in Sports and Exercise, 21, 78-83.
20. Morgan, D., Craib, M., Krahenbuhl, G., Woodall, K., Jordan, S., Filarski, K., Burleson, C. and Williams, T. (1994). Daily variability in running economy among well-trained male and female distance runners. Research Quar-terly, 65, 72-77.
21. Noakes, T., Myburgh, K. and Schall, R. (1990). Peak tread-mill velocity during the VO2 max test predicts running performance. Journal of Sports Sciences, 8, 35-45.
22. Powers, S., Dodd, S., Deason, R., Byrd, R. and McKnight, T. (1983). Ventilatory threshold, running economy and distance running performance of trained athletes. Research Quarterly for Sports and Exercise, 54, 179-182.
23. Pugh, L.G.C.E. (1970). Oxygen uptake in track and tread-mill running with observations on the effect of air resist-ance. Journal of Physiology, 207, 823-835.
24. Pugh, L.G.C.E. (1971). The influence of wind resistance in running and walking and the mechanical efficiency of work against horizontal or vertical forces. Journal of Physiology, 213, 225-276.
25. Ramsbottom, R., Brewer, J. and Williams, C. (1988). A progressive shuttle run test to estimate maximal oxygen uptake. British Journal of Sports Medicine, 22, 141-144.
26. Riggs, C.E., Johnson, D.J., Konopka, B.J. and Kilgour, R.D. (1981). Exercise heart rate response to facial cooling. European Journal of Applied Physiology; 47, 323-330.
27. Shephard, R. (1969). A nomogram to calculate the oxygen cost of running at slow speeds. Journal of Sports Medicine and Physical Fitness, 9, 10-16.
28. Tetgbur, U., Busse, M. and Braumann, K. (1993). Estimation of individual equilibrium between lactate production and catabolism during exercise. Medicine and Science in Sports and Exercise, 25, 620-627.
29. Van Ingen Schenau, G.J. (1980). Some fundamental aspects of the biomechanics of overground versus treadmill loco-motion. Medicine and Science in Sports and Exercise, 12, 257-261.
30. Weltman, A., Snead, D., Steim, P., Schurrer, R., Rutt, R. and Weltmann, J. (1990). Reliability and validity of a continuous incremental treadmill protocol for the determination of lactate threshold, fixed blood lactate concentrations and VO2 max. International Journal of Sports Medicine, 11, 26-32.
31. Williams, P.A. and Kilgour, R.D. (1993). Cardiovascular responses to facial cooling during low and moderate intensity exercise. European Journal of Applied Physiology, 67, 53-58.