Medida ± Desviación Estándar o ± Error Estándar de la Media

En esta oportunidad quisiéramos cambiar el foco de la discusión hacia un planteo realizado por el Dr. Hopkins en su sitio Web, www.sportsci.org. Antes que nada quisiéramos agradecer al Dr. Hopkins por autorizarnos a reproducir parte de sus escritos que consideramos extremadamente analíticos.

La desviación estándar (SD) representa la variación en los valores de una variable, mientras que el error estándar de la media (Estándar Error of the Mean, SEM) representa la dispersión que tendría la media de una muestra de valores si se continuaran tomando muestras. Por lo tanto, el SEM proporciona una idea de la precisión de la media y el SD nos da una idea de la variabilidad de las observaciones individuales. Estos dos parámetros están relacionados:

SEM = SD/√n

Donde:
SEM = Error estándar de la media
SD = Desviación estándar
n = tamaño de la muestra

Algunos consideran que deberían presentar el SEM con las medias debido a que creen que es importante indicar cuan precisa es la estimación de la media. Cuando se comparan dos medias suele argumentarse que al presentar el SEM se tiene una idea de si existe una diferencia estadísticamente significativa entre las medias. Todo muy bien pero, esto es lo que no va por el camino correcto:

• Para la estadística descriptiva de los sujetos, se debe presentar el SD para dar al lector una idea de la dispersión entre lo sujetos. Presentar el SEM con la media es absurdo.
  
• Cuando se comparan medias grupales, la presentación del SD proporciona una idea de la magnitud de las diferencias entre las medias, debido a que se puede observar cuán grande es la diferencia en relación con el SD. En otras palabras, se puede observar cuán grande es el tamaño del efecto.
  
• Es importante visualizar el SD cuando hay varios grupos experimentales, debido a que si el SD difiere en gran medida, se podría utilizar una transformación logarítmica o por rangos antes de computar los intervalos de confianza o los valores p. Si el número de sujeto difiere entre los grupos, el SEM no proporciona una impresión visual directa de si hay diferencias en el SD.
  
• Si pensamos que es importante indicar la significancia estadística, entonces se deben reportar los valores de p o los límites de confianza de los resultados estadísticos. Esto es mucho más preciso que reportar los valores del SEM. Además ¿Alguien sabe cuánto de los SEM deben superponerse o no superponerse para estipular que una diferencia es significativa? Asimismo ¿Alguien sabe si la magnitud de la superposición o no superposición depende del tamaño relativo de la muestra?
  
• Más importante aún, cuando se tienen valores medios para puntajes pre y post en un experimento con medidas repetidas, el SEM de estas medias NO proporciona una impresión de la significancia estadística del cambio – un punto sutil que desafía a muchos estadísticos. Por lo tanto, si el SEM no muestra significancia estadística en los experimentos ¿Cuál es el punto de presentarlos?
  

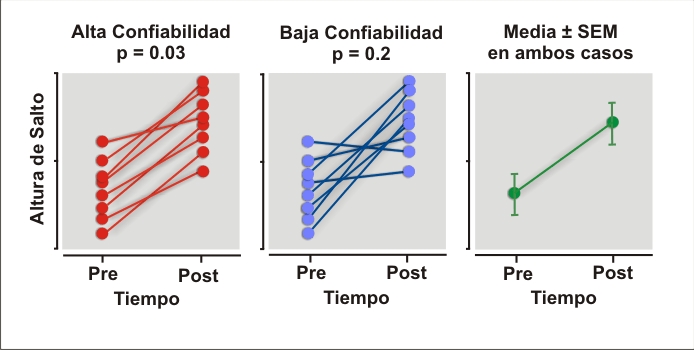
La Figura que se muestra a continuación ilustra por qué el SEM no expresa significancia estadística. La figura muestra datos imaginarios para un experimento que tiene como objetivo incrementar la altura de salto. El cambio en la altura de salto es significativo (p = 0.03) cuando la medición de la altura de salto tiene una alta confiabilidad, pero no es significativa (p = 0.2) cuando la confiabilidad es baja. Sin embargo, el SEM es el mismo en ambos casos.

El SEM de los cambios pre-post tratamiento en un grupo experimental y un grupo control “podrían” indicar significancia estadística. Pero si se muestran los valores de cambio, debería mostrar los intervalos de confianza para el cambio y NO el SEM. Se deberían también mostrar los SD para los valores de cambio en el grupo experimental y el grupo control, debido a que un substancial incremento en el SD de los valores de cambio en el grupo experimental y el grupo control indica las respuestas individuales al tratamiento. El SEM de los valores de cambio podría indicar la posibilidad de una respuesta individual solo si el tamaño de la muestra en ambos grupos es igual.

Por lo tanto, cuando observe un SEM en una publicación, sonría y mentalmente convierta estos valores en SD para observar cuan grandes son las diferencias entre los grupos. Por ejemplo, si la muestra consiste de 25 sujetos, aumente el valor del SEM por un factor de 5 (la raíz cuadrada de 25) y convierta estos valores en SD.

En definitiva: “Nunca muestre el SEM, nunca”

Will G Hopkins, PhD FACSM FECSS

Artículo Original/Original Article

Si bien muchos pueden considerar que estas temáticas no son importantes, creemos que en realidad sucede todo lo contrario. Actualmente la mayoría (por no decir todos), acceden a trabajos de investigación o se presentan conferencias o resultados de investigación para respaldar una práctica deportiva o una metodología específica. En la mayoría de los casos se presentan resultados indiscriminadamente, se muestran tablas, gráficas, etc., poniendo sobre la mesa discusiones acerca de si algo “sirve o no sirve” o simplemente citando trabajos de investigación. Lamentablemente pocas veces se discuten los resultados de las investigaciones en base a cuestiones como las que el Dr. Hopkins señala. En muy escasas oportunidades se presenta una investigación y se cuestionan los aspectos relacionados con los métodos utilizados y mucho menos se discute acerca de la estadística utilizada (con suerte solo se menciona que p fue mayor o menor a un “x” valor, y muchas veces ni siquiera esto se discute). Desafortunadamente la ciencia puede ser mal utilizada. En la actualidad vivimos en la era tecnológica y todo suele estar o “aparentar estar” respaldado por estudios de investigación. Sin embargo, si como docentes no inducimos al pensamiento crítico de los resultados experimentales, entonces considero que estamos tomando un camino equivocado. Considero que no basta simplemente con presentar una gráfica o una tabla de un estudio de investigación, hay que analizar el mismo en su contexto, en su metodología y a qué modelo teórico se recurre para el diseño experimental. Si no recurrimos al análisis crítico de los resultados experimentales dentro de un marco específico estamos entonces comercializando la ciencia.

Quisiera agradecer al Dr. Daniel Boullosa y al Lic. Adrián Barale, con quienes tuve el enorme placer de poder debatir estas cuestiones, y cuya perspectiva y análisis crítico me han alentado a buscar nuevos horizontes de conocimiento.

Un fuerte saludo

Sebastián Del Rosso