Predicción del Rendimiento en Carreras de Una Hora utilizando Tests de Duración Constante
François X Gamelin1, Laurent Bosquet1,4, Jéremy Coquart2, Nicolas Ferrari2, Hubert Vodougnon2, Régis Matran3 y Luc A Léger4
3Service des Explorations Fonctionnelles Respiratoires, Centre Hospitalier Universitaire, Hôpital Calmette, Lille, Francia.
4Département de Kinésiology, Université de Montréal, Montréal, Canadá.
Artículo publicado en el journal PubliCE, Volumen 0 del año 2006.
Publicado 18 de julio de 2007
Resumen
Palabras clave: velocidad crítica, modelos, resistencia, comparación
INTRODUCCION
Desde el clásico trabajo de Hill (10), se ha aceptado que la relación entre la producción de potencia y el tiempo hasta el agotamiento tiene una forma hiperbólica. La asintota de la potencia en esta relación, la cual por conversión es equivalente a la pendiente de la regresión lineal que relaciona el trabajo y el tiempo hasta el agotamiento, ha sido denominada por Monod y Scherrer (25) como potencia crítica (CP). Debido a que la potencia crítica representa, al menos teóricamente, la mayor producción de potencia que puede ser mantenida a través del metabolismo aeróbico sin alcanzar la fatiga, la CP es un buen índice de la capacidad de rendimiento en eventos de larga duración (2, 11, 32).
Ettema (6) aplicó el concepto de CP a la carrera sustituyendo la velocidad por la potencia y la distancia por el trabajo. La asintota de la velocidad de la relación hiperbólica entre la velocidad y el tiempo hasta el agotamiento o, por conversión, la pendiente de la relación entre la distancia y el tiempo hasta el agotamiento, denominada velocidad crítica (CV), tiene el mismo significado fisiológico que la CP (19, 20, 27).
La relación lineal entre la distancia y el tiempo hasta el agotamiento, y la relación no lineal entre la velocidad y el tiempo hasta el agotamiento, no son los únicos modelos matemáticos que permiten la estimación de la CV (18). Para evitar la suposición de que en el modelo hiperbólico la velocidad tiene a infinito cuando el tiempo tiende a cero, Hopkins et al (13) y Morton (26) propusieron dos modelos diferentes, incluyendo un parámetro adicional que representa la velocidad máxima (Vmáx.). Por su parte, Whipp et al. (33) propusieron una conversión lineal de la relación hiperbólica para relacionar la velocidad y la inversa del tiempo.
Los estudios diseñados para comparar la CV o la CP computadas a partir de estos 5 modelos matemáticos reportaron una diferencia de al menos 20% entre las estimaciones más altas y las más bajas (3, 8, 12, 18). Aunque la elección de la ecuación parece importante, la cuestión sigue abierta respecto de determinar cual de los modelos provee una estimación de la CV que esté más estrechamente relacionada con la capacidad de rendimiento en eventos de larga duración.
El interés en modelar la relación entre la distancia o la velocidad y el tiempo hasta el agotamiento va más allá de la simple estimación de la CV. De hecho, permite estimar individualmente el tiempo requerido para cubrir una distancia determinada, o por conversión, la velocidad que puede ser mantenida en un tiempo determinado. Dichos datos son de gran interés para los entrenadores que desean predecir el rendimiento de sus atletas o prescribir intensidades de entrenamiento, especialmente para corredores de media y larga distancia. En efecto, un método para mejorar el rendimiento en carreras de larga duración es entrenar a la velocidad de carrera (9). Con excepción del estudio de Hughson et al. (20), quienes hallaron que el rendimiento estimado a partir del modelo hiperbólico para una carrera de 10 km sobreestimaba el rendimiento real, no se han hecho intentos por valorar la precisión de las estimaciones realizadas a partir de los parámetros individuales de cada modelo para carreras de larga duración.
El propósito del presente estudio fue doble: (a) determinar cual es la estimación de la CV que mejor predice el rendimiento en un evento de larga duración y (b) comparar el rendimiento real con el rendimiento estimado a partir de parámetros individuales, para determinar el valor predictivo de cada modelo.
METODOS
Enfoque Experimental al Problema
Todos los sujetos realizaron tres tests de duración constante y un test a la velocidad máxima de carrera para la estimación de la CV. Los test de duración constante fueron llevados a cabo aleatoriamente, y el intervalo de tiempo entre los tests fue de al menos 24 horas. La velocidad máxima de carrera fue adicionada aleatoriamente a uno de los test de duración constante. Los sujetos alcanzar la máxima velocidad de carrera con el mismo calzado utilizado en los tests de duración constante. Los sujetos también realizaron un test de carrera de 1 hora en la pista de atletismo (rendimiento real) para comparar el rendimiento estimado con el rendimiento real. Todos los tests se realizaron dentro del período de 7 semanas previas al tests de carrera de una hora. Los sujetos evitaron realizar actividades físicas vigorosas por al menos 24 horas antes del test, y fueron instruidos para que realizaran la misma ingesta nutricional. En el presente estudio se utilizaron corredores bien entrenados que eran capaces de correr durante una hora y de adaptar su velocidad de carrera durante los tests para obtener el mejor rendimiento.
Sujetos
Doce corredores varones bien entrenados dieron su consentimiento informado por escrito para participar en el presente estudio. Su edad, talla y peso medio (±DE) fueron de 29±5 años, 177±7 cm y 70±8 kg. Todos los participantes eran corredores de media y larga distancia que habían estado entrenando más de 4 días semanales por al menos tres años. Durante el año en que se llevó a cabo el estudio, el valor medio del récord para la carrera de 10 km en este grupo de corredores fue de 37.7±2.7 minutos. Todos los sujetos fueron sometidos a un protocolo de inclusión antes de comenzar con las pruebas experimentales. Este protocolo consistió en una sesión de información referente a la naturaleza, riesgos potenciales y a los beneficios del estudio, seguida de una revisación médica para aquellos que estuvieran interesados en participar del estudio. Luego de esto todos los sujetos dieron su consentimiento informado antes de ser incluidos en el estudio. El protocolo fue revisado y aprobado por el Comité para la Protección de Sujetos Humanos en la Investigación Biomédica de Nord Pas de Calais, Francia.
Tests de Duración Constante
Para determinar el tiempo hasta el agotamiento a la CV, lo cual ocurre dentro de los 3 y los 30 minutos (32), los sujetos realizaron en forma aleatoria 3 tests de duración constante de 6, 9 y 12 minutos de duración realizados en una pista sintética techada de 200 metros, llevándose a cabo los tres tests a la misma hora del día (entre las 5.00 PM y las 8.00 PM). Se les instruyó a los sujetos que cubrieran la mayor distancia posible en el período de tiempo establecido. La distancia fue medida con una precisión de 5 metros. Cada test fue precedido por una entrada en calor estandarizada que consistió de 10 minutos de carrera a ritmo individual, 5 min de estiramientos y 5 aceleraciones de 100 metros con 1 min de pausa pasiva entre cada carrera.
Test a la Máxima Velocidad de Carrera
Se realizaron dos pruebas de 30 metros lanzados con una carrera previa de 20 metros separadas por un período de recuperación pasiva de 5 minutos en una pista sintética techada de 200 metros. La entrada en calor que precedió a la primera prueba fue similar a la entrada en calor que precedió a los tests de duración constante. La velocidad fue medida con fotocélulas (IRE and IRD-T175; Brower Timing Systems, Salt Lake City, UT) colocadas a los 20 y 50 metros. El tiempo fue controlado telemétricamente con un cronómetro (CM 705 CR; Brower Timing Systems). La altura de las fotocélulas fue ajustada para que el haz de luz estuviera a la altura de las caderas de los sujetos. La velocidad media en la mejor prueba de 30 metros fue considerada la Vmáx.
Test de Rendimiento
Los sujetos participaron en un evento de 1 hora, el cual fue llevado a cabo en una pista de atletismo sintética de 400 metros. En el presente estudio se optó por este evento ya que es representativo de los diferentes eventos en los que participaban nuestros sujetos durante sus competencias (10 a 21.1 km). Nuevamente, se les instruyó a los sujetos que cubrieran la mayor distancia posible durante los 60 min de competencia. La distancia fue medida con una precisión de 10 m.
Modelo Matemático
El rendimiento en los tests de duración constante y, cuando fuera apropiado, en los tests de velocidad máxima fue ajustado a cada uno de los 5 modelos utilizados por Housh et al. (18) para estimar la CV:
El Modelo Hiperbólico Clásico
El modelo hiperbólico clásico, propuesto en primer lugar por Hill (10), utiliza la regresión entre el tiempo (t) y la velocidad (v), por lo tanto: t = ARC/(v – CV) (1) donde t representa el tiempo (segundos), ARC es la capacidad anaeróbica (metros) y CV es la velocidad crítica (m/s).
La Reformulación Lineal
La reformulación lineal, propuesta por Monod y Scherrer (25), utiliza la regresión entre la distancia (d) y el tiempo (t), por lo tanto: d = CV.t + ARC (2).
El Modelo Lineal Alternativo
El modelo lineal alternativo, propuesto por Whipp et al. (33) utiliza la regresión entre la velocidad (v) y la inversa del tiempo (1/t), por lo tanto: v = ARC.(1/t) + CV (3)
El Modelo de 3 Parámetros
El modelo de 3 parámetros, propuesto por Morton (26), utiliza la regresión entre el tiempo (t), la velocidad (v) con la adición de un tercer parámetro que representa la Vmáx. expresada en m/s, por lo tanto: t = ARC/(v – CV) – ARC/(Vmáx. – CV) (4)
El Modelo Exponencial
El modelo exponencial, propuesto por Hopkins et al. (13), utiliza la regresión entre el tiempo (t) y la velocidad (v) con la adición de la Vmáx., por lo tanto: v = CV + (Vmáx. – CV).e(-τ/r) (5) donde τ es una constante de tiempo no definida (segundos).
Predicción del Rendimiento
Los parámetros individuales de cada modelo fueron utilizados para predecir la velocidad (Ecuaciones 1, 3-5) o la distancia (Ecuación 2) que los sujetos podrían mantener o cubrir durante el evento de una hora. En el caso de la Ecuación 2, la distancia fue dividida por la duración del evento (3600 segundos) para obtener la velocidad y hacer las comparaciones correspondientes con los otros 4 modelos.
Análisis Estadísticos
Se utilizaron métodos estadísticos estándar para calcular las medias y las desviaciones estándar. Los coeficientes de determinación fueron calculados para determinar cuan buenos eran los ajustes de los datos de los modelos. Se utilizó un modelo lineal general para mediciones repetidas, para evaluar las diferencias en los valores medios de CV y en el rendimiento promedio estimado con los 5 modelos. Se utilizó el test de Shapiro-Wilk para verificar que los datos tuvieran una distribución Gaussiana normal. Se utilizó el test de Mauchely para evaluar la hipótesis de simetría o esfericidad. Debido a que no se cumplió la hipótesis de esfericidad, la significancia de los estadísticos F se ajustó de acuerdo con el procedimiento de Greenhouse-Geisser cuando el factor de corrección épsilon fue <0.75 o de acuerdo al procedimiento de Huyn-Feld cuando el factor de corrección épsilon fue >0.75. Se realizaron comparaciones múltiples utilizando el test post hoc de Bonferroni. Luego de verificar la homocedasticidad con el test de Lavenne, se utilizó la prueba t para datos apareados para evaluar la diferencia entre el rendimiento real y el rendimiento estimado por cada modelo. La magnitud de esta diferencia fue valorada mediante el tamaño del efecto. Debido a que no hubo un grupo que actuara como control per se, se utilizó el conjunto de las desviaciones estándar para computar este estadístico. Para la interpretación se utilizó la escala propuesta por Cohen (5). La magnitud de la diferencia fue considerada pequeña (0.2), moderada (0.5) o grande (0.8). Para cada modelo se calculó el intervalo de confianza del 95% para la diferencia entre el rendimiento real y el rendimiento estimado. Se utilizó la correlación momento producto de Pearson para evaluar la asociación entre el rendimiento real y la CV o el rendimiento estimado.
La significancia estadística fue establecida a un nivel p≤0.05. Todos los análisis estadísticos fueron llevados a cabo con el programa Statistica (version 6.0; Statsoft, Tulsa, OK).
RESULTADOS
Velocidad Crítica
Los valores medios de la CV estimada por los 5 modelos, así como también la
bondad del ajuste en la correlación con el rendimiento se presentan en la Tabla
1. Los tests post hoc de Bonferroni revelaron que tanto las estimaciones de la
CV por el modelo No Lineal de 3 parámetros (la menor) y EXP (la mayor) fueron
significativamente diferente de los otros modelos. Aunque todas las estimaciones
de la CV estuvieron significativamente correlacionadas entre sí (0.85
Predicción del Rendimiento La velocidad media sostenida por los sujetos durante el test de carrera en
pista de una hora (i.e., rendimiento real) fue de 4.27±0.23 m/s. El rendimiento
medio estimado por los 5 modelos, como así también la correlación con el
rendimiento real, los sesgos, el intervalo de confianza del 95% para el sesgo, y
la magnitud de la diferencia, se presentan en la Tabla 2. Al parecer los 5
modelos arrojaron predicciones que podrían diferir significativamente una de
otra. El modelo No Lineal de 3 parámetros, fue el único modelo que arrojó una
predicción que no difirió significativamente del rendimiento real (se interpretó
que la magnitud de la diferencia era pequeña). Sin embargo, el intervalo de
confianza del 95% fue bastante grande (0.13±0.55 m/s, lo cual representa el
12.9% del rendimiento real). Por el contrario, el sesgo en el modelo EXP fue
grande, pero el intervalo de confianza del 95% fue el menor (0.48±0.28 m/s, lo
cual representa el 6.9% del rendimiento real).
La CV puede computarse a partir del rendimiento en tres tipos de tests: tests
de trabajo constante (CWT), tests de duración constante (CDT) y tests de
potencia constante (CPT) (16). La mayoría de los estudios han utilizado 2 a 6
CPT para determinar la CV (7, 18, 19, 20, 22-24, 27, 31). Sin embargo,
considerando la confiabilidad del estudio de Jeukendrup et al. (21), quien
reportó un coeficiente de variación del 26.6% para los tests CPT, del 3.5% para
los tests CDT y del 3.4% para los tests CWT, nosotros optamos por utilizar los
tests CDT en lugar de CPT. Esta elección fue confirmada por Schabort et al.
(29), quienes observaron un coeficiente de variación del 2.7% y un coeficiente
de correlación intraclase de 0.90 para un test CDT de una hora.
Como lo señalan varios autores (1, 4, 32), la elección de un determinado
rango de duración es particularmente importante para estimar la CV. Los
lineamientos clásicos recomiendan que la menor duración no debe ser menor a 3
minutos, mientras que la prueba de mayor duración no debería exceder los 30
minutos (1, 32). Vale la pena señalar que en la mayoría de los estudios no se
utilizan pruebas de más de 12 minutos de duración (18, 19, 20, 23). Además,
debería haber al menos 5 minutos entre la prueba más corta y la más larga (17).
El rango de duración utilizado en el presente estudio concuerda con estas
recomendaciones.
Si bien la estimación del parámetro a partir de los modelos lineales no está
influenciada por la designación de las variables dependientes e independientes
cuando el coeficiente de correlación es alto (28), esto no parece ser igual para
los modelos no lineales (8). Para asegurar la consistencia con la literatura, en
los modelos no lineales de 2 y 3 parámetros, el tiempo fue asignado como
variable dependiente, mientras en los 3 modelos restantes se utilizó la
velocidad (Modelos Lineal-V y EXP) o la Velocidad.t (Lineal-TD) (8).
La bondad de ajuste de los datos en los 5 modelos (0.97±0.03 El primer objetivo del presente estudio fue determinar cual estimación de la
CV predecía de mejor manera el rendimiento en un evento de una hora en pista de
atletismo. Como ya lo habían reportado Housh et al. (17) para la CV, y Gaesser
et al. (8) y Bull et al. (3) para la CP, nosotros hallamos que el modelo no
lineal de 3 parámetros arrojó el menor valor medio de CV, mientras que el modelo
EXP produjo la estimación más alta (Tabla 1). No se hallaron diferencias entre
los modelos Lineal-TD, Lineal-V y No Lineal 2. Todas las estimaciones de la CV
estuvieron correlacionadas unas con otras, pero también con el rendimiento
(Tabla 1). Las correlaciones observadas en nuestro estudio son del mismo orden
de magnitud que los valores reportados por Kolbe et al. (23) entre el
rendimiento estimado por el modelo EXP y el rendimiento real en una carrera de
10 km (r=0.85) y de 21.1 km (r=0.79), por Kranenburg y Smith (24) entre el
rendimiento estimado por el modelo Lineal-V y el rendimiento real en una carrera
de cross country de 9.8 km (r=0.92) o por Florence y Weir (7) entre el
rendimiento estimado por el modelo Lineal-TD y el rendimiento real en una
maratón (r=0.87). Gaesser et al. (8) sugirieron, en base a consideraciones tanto estadísticas
como fisiológicas, que el modelo No Lineal de 3 parámetros debería ser el
preferido a la hora de estimar tanto la CV como la ARC. Si bien nuestros
resultados demuestran que la estimación de la CV por el modelo No Lineal de 3
parámetros tuvo una buena correlación con el rendimiento (r=0.80), también
indican que no es el mejor predictor, ya que las correlaciones observadas con
todas las otras estimaciones de la CV son mayores (Tabla 1). Al parecer la CV
derivada con el modelo EXP está más estrechamente vinculada con el rendimiento
(r=0.93) que la CV derivada con todos los otros modelos. Tal como ya lo
señalaran Gaesser et al. (8) y Bull et al. (3), la ponderación respectiva de
cada modelo puede verse afectada por las diferencias en la selección de las
variables dependientes e independientes, la expresión de las variabes (t vs.
1/t) o el número de variables de cada modelo. Si bien la explicación matemática
exacta de esta diferencia todavía debe ser dilucidada, el hecho es que la CV
derivada con el modelo EXP parece ser el mejor predictor del rendimiento en un
evento de una hora que las otras estimaciones de la CV en corredores varones
bien entrenados.
El segundo objetivo del presente estudio fue comparar el rendimiento real con
el rendimiento estimado a partir de los parámetros individuales para determinar
el valor predictivo de cada modelo. Todos los modelos, excepto el modelo No
Lineal de 3 parámetros arrojaron estimaciones que fueron significativamente
mayores que el rendimiento real. La magnitud de estas diferencias fue pequeña
(No Lineal de 3 parámetros), moderada (Lineal-TD, Lineal-V, No Lineal de 2
parámetros), o grande (EXP). Hughson et al. (20) ya habían reportado dichas
diferencias, ya que estos investigadores hallaron que el rendimiento estimado
con el modelo No Lineal de 2 parámetros para una carrera de 10 km era
significativamente mayor que el rendimiento real.
Parte de la diferencia observada en nuestro estudio probablemente se debió a
diferencias en las condiciones experimentales. De hecho, los tests CDT fueron
llevados a cabo en una pista sintética cubierta de 200 metros (i.e., sin viento)
mientras que el evento de una hora fue llevado a cabo en una pista sintética de
400 metros al aire libre con condiciones de temperaturas frescas pero con
viento, lo cual pudo haber provocado la reducción del ritmo de carrera.
Cualquiera sea la duración del evento, tanto los modelos lineales como los no
lineales no pueden predecir una velocidad menor que la CV. Los resultados
disponibles en la literatura claramente demuestran que la CV no es la intensidad
que puede ser mantenida por un período de tiempo prolongado sin llegar a la
fatiga (25). Dependiendo del modelo utilizado para estimar la CV y el número y
la duración de las pruebas utilizadas para la estimación, se ha reportado que el
tiempo hasta el agotamiento a la CV varía desde 16.43±6.08 minutos (27) hasta
57.7±9.9 minutos (28). La consecuencia es la estimación de un valor bajo para
eventos de una hora o más de duración, ya que la velocidad media sostenida
durante estos eventos es generalmente menor que la CV, resultando en una
sobreestimación del rendimiento.
La mejora mínima del rendimiento que tiene un efecto substancial respecto de
la oportunidad de un atleta de élite de ganar es aproximadamente un tercio de la
variación característica del rendimiento de competición (14), lo cual es
aproximadamente el 1% para la media maratón y la maratón (15). Con los límites
de confianza del 95% que representan el 7-13% del rendimiento actual, el
potencial error de utilizar dichas estimaciones es demasiado grande como para
detectar dicho efecto.
Los objetivos del presente estudio fueron dos: (a) determinar cual estimación
de la CV derivada con los 5 modelos matemáticos generalmente utilizados en la
literatura es el mejor predictor del rendimiento en un evento de una hora y (b)
examinar el valor predictivo de cada modelo mediante la comparación del
rendimiento real y el rendimiento estimado a partir de parámetros individuales.
Al parecer nuestros resultados indican que la CV derivada con el modelo EXP está
más estrechamente asociada con el rendimiento que la CV derivada con los otros
modelos. Por otra parte, ninguno de estos modelos parece estar en posición de
predecir el rendimiento con suficiente precisión como para detectar efectos
significativos en eventos de larga distancia.
Aplicaciones Prácticas Este estudio ha mostrado que ningún modelo para la estimación de la CV
permite estimar el rendimiento en una carrera de una hora. Generalmente, para
mejorar el rendimiento, se prescriben sesiones de entrenamiento a la velocidad
de competición. Por lo tanto, no se recomienda que los entrenadores o los
atletas consideren la velocidad estimada por alguno de estos modelos como la
velocidad de competencia. Sin embargo, en este estudio, la predicción del
rendimiento y la CV estuvieron fuertemente correlacionadas (r ≥0.80, p<0.01) con
el rendimiento real, sin tener en cuenta que modelo se haya utilizado. En
efecto, la CV está más estrechamente asociada con el rendimiento en una maratón
que con el consumo máximo de oxígeno. Por lo tanto, la estimación de la CV es
más sensible a la capacidad individual de obtener buenos rendimientos en eventos
de una hora que con el consumo máximo de oxígeno ( VO2 máx). En general, los
entrenadores clasifican a sus atletas con referencia a su consumo máximo de
oxígeno, pero este parámetro no es determinante en eventos de larga duración.
Durante estos eventos los atletas deben mantener un alto porcentaje del VO2 máx
a través de todo el evento (e.g., resistencia aeróbica). La estimación de la CV
tiene en cuenta el VO2 máx y la resistencia aeróbica. Si bien la CV derivada con
el modelo EXP está más estrechamente asociada con el rendimiento que la CV
derivada con los otros modelos; el calculo de la CV obtenido con el modelo
Lineal-TD es relativamente más fácil de valorar, ya que solo se requieren dos
tests de campo y dos tests de rendimiento. La CV fue calculada como la pendiente
de la regresión lineal o distancia vs. tiempo. De esta manera, la CV derivada
con el modelo Lineal-TD nos permite clasificar a corredores de media y larga
distancia con respecto a su capacidad para obtener buenos rendimientos en
carreras de media y larga distancia y no solo con referencia a su VO2máx.
Agradecimientos Los autores están en deuda con el Consejo Regional de Nord Pas de Calais por
su respaldo financiero. Este estudio cumple con las leyes actuales de Francia. Dirección para el Envío de Correspondencia François-Xavier Gamelin, correo electrónico: fxgamelin@hotmail.com. 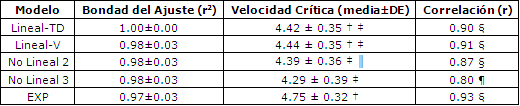
Tabla 1. Velocidad crítica (m/s), bondad de ajuste (r2) y coeficiente de
correlación (r) de la velocidad crítica vs. el rendimiento en un evento de 1
hora para los 5 modelos. Lineal-TD = la formulación lineal; Lineal-V = el modelo
lineal alternativo; No Lineal 2 = el modelo clásico hiperbólico; No Lineal 3 =
el modelo de 3 parámetros; EXP = el modelo exponencial. †Significativamente
diferente del modelo No Lineal 3 (p<0.01), ‡ Significativamente diferente del
modelo EXP (p<0.0001), § p<0.001. ║significativamente diferente del modelo No
Lineal 3 (p<0.05), ¶ p<0.01.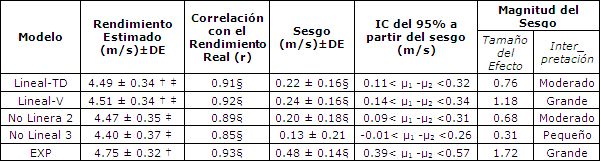
Tabla 2. Rendimiento estimado, correlación con el rendimiento real, sesgo,
magnitud del sesgo e intervalo de confianza del 95% (IC) para el sesgo en los 5
modelos. Sesgo = diferencia entre el rendimiento estimado y el rendimiento real;
IC del 95% = intervalo de confianza del 95%; μ1 y μ2 = medias paramétricas para
el rendimiento estimado y real, respectivamente. Lineal-TD = la formulación
lineal; Lineal-V = el modelo lineal alternativo; No Lineal 2 = el modelo clásico
hiperbólico; No Lineal 3=El modelo de 3 parámetros; EXP = el modelo exponencial.
† Significativamente diferente del modelo No Lineal 3 (p<0.01), ‡
Significativamente diferente del modelo EXP (p<0.0001), § p<0.001.DISCUSION
Referencias
1. Bishop, D., D.G. Jenkins, and A. Howard (1998). The critical power function is dependent on the duration of the predictive exercise tests chosen. Int. J. Sports Med. 19:125129
2. Bosquet, L., L. Leger, and P. Legros (2002). Methods to determine aerobic endurance. Sports Med. 32:675700
3. Bull, A.J., T.J. Housh, G.O. Johnson, and S.R. Perry (2000). Effect of mathematical modeling on the estimation of critical power. Med. Sci. Sports Exerc. 32:526530
4. Clingeleffer, A., L. McNaughton, and B. Davoren (1994). Critical power may be determined from two tests in elite kayakers. Eur. J. Appl. Physiol. Occup. Physiol. 68:3640
5. Cohen, J (1988). Statistical Power Analysis for the Behavioral Sciences. Hillsdale: Lawrence Erlbaum Associates
6. Ettema, J.H (1966). Limits of human performance and energy production. Int. J. Z. Angew Physiol. Einschl. Arbeitphysiol. 22:4554
7. Florence, S., and J.P. Weir (1997). Relationship of critical velocity to marathon running performance. Eur. J. Appl. Physiol. Occup. Physiol. 75:274278
8. Gaesser, G.A., T.J. Carnevale, A. Garfinkel, D.O. Walter, and C.J. Womack (1995). Estimation of critical power with nonlineal and lineal models. Med. Sci. Sports Exerc. 27:14301438
9. Hawley, J.A., K.H. Myburgh, T.D. Noakes, and S.C. Dennis (1997). Training techniques to improve fatigue resistance and enhance endurance performance. J. Sports Sci. 15:325333
10. Hill, A.V (1997). Muscular Movement in Man: The Factors Governing Speed and Recovery from Fatigue. New York: McGraw-Hill
11. Hill, D.W (1993). The critical power concept. A review. Sports Med. 16:237254
12. Hill, D.W., C. Alain, and M.D. Kennedy (2003). Modeling the relationship between velocity and time to fatigue in rowing. Med. Sci. Sports Exerc. 35:20982105
13. Hopkins, W.G., I.M. Edmond, B.H. Hamilton, D.J. MacFarlane, and B.H. Ross (1989). Relation between power and endurance for treadmill running of short duration. Ergonomics. 32:15651571
14. Hopkins, W.G., J.A. Hawley, and L.M. Burke (1999). Design and analysis of research on sport performance enhancement. Med. Sci. Sports Exerc. 31:472485
15. Hopkins, W.G., and D.J. Hewson (2001). Variability of competitive performance of distance runners. Med. Sci. Sports Exerc. 33:15881592
16. Hopkins, W.G., E.J. Schabort, and J.A. Hawley (2001). Reliability of power in physical performance tests. Sports Med. 31:211234
17. Housh, D.J., T.J. Housh, and S.M. Bauge (1990). A methodological consideration for the determination of critical power and anaerobic work capacity. Res. Q. Exerc. Sport. 61:406409
18. Housh, T.J., J.T. Cramer, A.J. Bull, G.O. Johnson, and D.J. Housh (2001). The effect of mathematical modeling on critical velocity. Eur. J. Appl. Physiol. 84:469475
19. Housh, T.J., H.A. DeVries, D.J. Housh, M.W. Tichy, K.D. Smyth, and A.M. Tichy (1991). The relationship between critical power and the onset of blood lactate accumulation. J. Sports Med. Phys. Fitness. 31:3136
20. Hughson, R.L., C.J. Orok, and L.E. Staudt (1984). A high velocity treadmill running test to assess endurance running potential. Int. J. Sports Med. 5:2325
21. Jeukendrup, A., W.H. Saris, F. Brouns, and A.D. Kester (1996). A new validated endurance performance test. Med. Sci. Sports Exerc. 28:266270
22. Kachouri, M., H. VandeWalle, V. Billat, M. Huet, M. Thomaidis, E. Jousselin, and H. Monod (1996). Critical velocity of continuous and intermittent running exercise. An example of the limits of the critical power concept. Eur. J. Appl. Physiol. Occup. Physiol. 73:484487
23. Kolbe, T., S.C. Dennis, E. Selley, T.D. Noakes, and M.I. Lambert (1995). The relationship between critical power and running performance. J. Sports Sci. 13:265269
24. Kranenburg, K.J., and D.J. Smith (1996). Comparison of critical speed determined from track running and treadmill tests in elite runners. Med. Sci. Sports Exerc. 28:614618
25. Monod, H., and J. Scherrer (1965). The work capacity of a synergistic muscular group. Ergonomics. 8:329338
26. Morton, R.H (1996). A 3-parameter critical power model. Ergonomics. 39:611619
27. Pepper, M.L., T.J. Housh, and G.O. Johnson (1992). The accuracy of the critical velocity test for predicting time to exhaustion during treadmill running. Int. J. Sports Med. 13:121124
28. Poole, D.C., S.A. Ward, and B.J. Whipp (1990). The effects of training on the metabolic and respiratory profile of high-intensity cycle ergometer exercise. Eur. J. Appl. Physiol. Occup. Physiol. 59:421429
29. Schabort, E.J., W.G. Hopkins, and J.A. Hawley (1998). Reproducibility of self-paced treadmill performance of trained endurance runners. Int. J. Sports Med. 19:4851
30. Sid-Ali, B., H. VandeWalle, K. Chair, A. Moreaux, and H. Monod (1991). Lactate steady state velocity and distance-exhaustion time relationship in running. Arch. Int. Physiol. Biochim. Biophys. 99:297301
31. Smith, C.G., and A.M. Jones (2001). The relationship between critical velocity, maximal lactate steady-state velocity and lactate turnpoint velocity in runners. Eur. J. Appl. Physiol. 85:1926
32. VandeWalle, H., J.F. Vautier, M. Kachouri, J.M. Lechevalier, and H. Monod (1997). Work-exhaustion time relationships and the critical power concept. A critical review. J. Sports Med. Phys. Fitness. 37:89102
33. Whipp, B.J., D.J. Huntsman, T. Storer, N. Lammarra, and K. Wasserman (1982). A constant which determines the duration of tolerance to high intensity work. Fed. Proc. 41:1591