Un Modelo de los Efectos del Viento y la Altura en la Carrera de 110 Metros con Vallas
Joshua Spiegel1 y Jonas R Mureika1
W. M. Keck Science Center, The Claremont Colleges, 925 N. Mills Avenue, Claremont, California USA.
Artículo publicado en el journal PubliCE, Volumen 0 del año 2003.
Publicado 10 de agosto de 2007
Resumen
Palabras clave: atletismo, récord mundial
INTRODUCCION
Los modelos matemáticos que dan cuenta de los efectos del arrastre aerodinámico en eventos de esprints cortos han sido un tema popular de investigación durante varios años. Hasta ahora, se le ha prestado mayor interés a los esprints cortos, siendo Davies (1980), Dapena y Feltner (1987), Keller (1974), Linthorne (1994), Mureika (2001, 2003) y Ward-Smith (1984, 1985, 1997, 1999) los investigadores que más han contribuido a este tema. En el presente estudio hemos aplicado el modelo de cuatro componentes de Mureika (2001), el cual incluye términos matemáticos que representan los efectos fisiológicos y físicos, modificado ligeramente para reflejar las diferencias en la carrera de 110m con vallas. Mureika propuso una ecuación para el movimiento de un velocista que incluye cuatro términos:
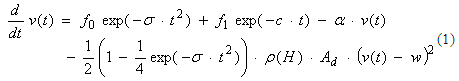
El primer término se denomina término de impulso (drive), el cual dominará durante los primeros segundos de la carrera pero luego caerá debido al exponente negativo de segundo orden. El coeficiente f0 es la magnitud de este término, y representa la fuerza por unidad de masa. El valor de σ controla la severidad del decaimiento exponencial. Debido a las restricciones de la carrera con vallas, es probable que f0 sea menor que el valor hallado por Mureika (2001) para la carrera de 100 metros.
El segundo término se denomina término de mantenimiento, y describe la habilidad del corredor para mantener consistentemente la misma fuerza de propulsión. El coeficiente f1 es la magnitud de este término (también representa la fuerza por unidad de masa), mientras que c sirve como una medida de la resistencia del corredor. Las diferencias entre la carrera con vallas y la carrera sin vallas deberían hacer que f1 sea menor que el valor utilizado en el ejemplo de Mureika (2001), mientras que c debería ser ligeramente mayor debido al esfuerzo extra que se requiere para sortear las vallas.
El tercer término es denominado término de velocidad y provee un límite superior a la máxima velocidad que puede alcanzar el corredor. Se basa en el principio de que debe existir cierto límite impuesto por consideraciones fisiológicas. El coeficiente α es responsable de la severidad de este límite. En el modelo de Mureika (2001), la frecuencia de zancada fue considerada un factor de importancia. Vern Gambetta en Brüggemann y Glad (1988) realizó los siguientes comentarios acerca de la zancada en un corredor de 110 con vallas: debido a la ubicación de las vallas, los corredores están limitados a cierto patrón de carrera. Entre el apoyo y el siguiente despegue, un vallista de sexo masculino debe completar tres zancadas de entre 1.88 y 1.99 metros. Esta distancia es substancialmente menor que la zancada promedio de 2.5 m observada en los sujetos que corren los 100 m planos. Debido a que las vallas representan una limitación particular a la longitud de zancada, los valores de α hallados aquí serán ligeramente mayores que el valor utilizado en el modelo de la carrera de 100 metros.
Se debería señalar que la dependencia del rendimiento en la carrera con vallas en la longitud de zancada podría ser una limitación de la aplicabilidad del modelo. Las condiciones ambientales podrían tener un substancial efecto sobre el rendimiento del atleta, y sería razonable asumir que la zancada en si misma pueda ser afectada en formas que aquí no son tenidas en cuenta. En el presente estudio supondremos que el patrón de zancada se mantiene constante en toda la carrera.
El último término del modelo, denominado término de arrastre, da cuenta de la fuerza extra que debe ejercerse debido a la velocidad del viento, la cual es afectada por la densidad del aire y el área de sección cruzada del corredor. El modelo para la carrera con vallas diferirá del modelo original en que el área de sección cruzada del vallista no es constante (aun aproximadamente) a través de la carrera. El coeficiente Ad puede ser considerado como el arrastre por unidad de masa. Para los propósitos del modelo, se asumió que el área de sección cruzada cae dentro del 60% del normal cuando el corredor se encuentra en la mitad del salto. Por lo tanto, a partir del valor de Ad= 0.00288 m2 dado por Mureika (2001) se derivó un valor de Asmall= 0.00173 que se utiliza en la Ecuación 2. Se asumió que el área de sección cruzada adopta solo dos valores, siendo el menor el expuesto para el tiempo característico necesario para sortear una valla y que es del orden de los 0.3 s (Müller, 1997). El coeficiente ρ(H) es la densidad del aire en función de la altura en g/m3, y cuyo cálculo de tomó directamente del trabajo de Mureika (2001). Se esperó que tanto este valor como el valor del área de sección cruzada tuvieran un efecto ligeramente mayor sobre el tiempo de carrera debido a los períodos en los cuales el arrastre es la única fuerza que actúa sobre el corredor. Este comportamiento se observó en los resultados.
El término
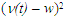 es la velocidad relativa del viento en m/s. Los valores positivos de
es la velocidad relativa del viento en m/s. Los valores positivos de
 indican que el componente de velocidad del viento se encuentra paralelo a la
dirección de la carrera y directamente con el atleta, i.e., viento a favor.
Observese que a medida que el valor de
indican que el componente de velocidad del viento se encuentra paralelo a la
dirección de la carrera y directamente con el atleta, i.e., viento a favor.
Observese que a medida que el valor de
 se vuelve más positivo, el efecto del arrastre se vuelve menor. El viento en
contra, indicado por un valor negativo de
se vuelve más positivo, el efecto del arrastre se vuelve menor. El viento en
contra, indicado por un valor negativo de
 ,
tiende a incrementar el efecto del arrastre en el modelo.
,
tiende a incrementar el efecto del arrastre en el modelo.
Cuando el corredor salta para sortear una valla, solo actúa la fuerza de arrastre. Por lo tanto, las otras tres fuerzas se turnan en forma periódica. Nosotros asumimos que no se requiere de una fuerza adicional significativa para sortear una valla, debido a que la fuerza ejercida durante la zancada es suficiente para proveer el impulso necesario. Durante los períodos en que se sortean las vallas la ecuación de movimiento es la siguiente:
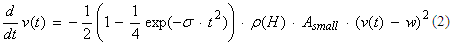
Cada término en (1) y (2) está sujeto a ciertos coeficientes, cuyos valores apropiados se determinan como se describe en la siguiente sección. Luego utilizaremos estos parámetros en el modelo para simular el rendimiento en la carrera de 110m con vallas bajo diversas condiciones de viento y altitud para determinar en que medida se verán afectado los tiempos de carrera. Estas correcciones serán aplicadas a los mejores tiempos registrados para esta prueba de forma tal que se pueda estudiar en que manera las condiciones ambientales han ayudado o perjudicado al establecimiento de los récords en esta prueba.
METODOS
En el presente estudio utilizamos la integración para resolver el siguiente par de ecuaciones diferenciales que definen el movimiento del atleta:
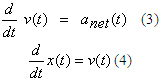
La Ecuación (3) representa una forma general de las Ecuaciones (1) y (2),
donde la apropiada elección de (1) o (2) se adopta en el algoritmo numérico de
integración. El lector podría reconocer las Ecuaciones (3) y (4) nada más que
como ecuaciones de movimiento que pueden ser resueltas para la posición
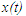 y la velocidad
y la velocidad
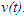 Para la integración numérica (ver e.g., Press, 1993), en el presente estudio
hemos utilizado el método estándar de cuarto orden de Runge – Kutta – Fehlberg
con un tiempo inicial de apoyo de 0.05 segundos. Para cada apoyo, se
determinaron la velocidad y la posición mediante la resolución del sistema de
ecuaciones. Cuando la posición fue igual a una de las ubicaciones de las vallas,
la ecuación para la fuerza neta fue modificada tal como se describe en la
Ecuación 2. Gambetta estimó que la zancada en la carrera con vallas, la
distancia entre un apoyo y el despegue, era de entre 3.15 y 3.50 m (Brüggemann
and Glad, 1988). En este modelo utilizamos un promedio de estos dos valores:
3.33 metros. Para cada apoyo, se registraron el tiempo y la velocidad de manera
tal que se pudieran comparar con los tiempos parciales obtenidos en las
competiciones.
Para la integración numérica (ver e.g., Press, 1993), en el presente estudio
hemos utilizado el método estándar de cuarto orden de Runge – Kutta – Fehlberg
con un tiempo inicial de apoyo de 0.05 segundos. Para cada apoyo, se
determinaron la velocidad y la posición mediante la resolución del sistema de
ecuaciones. Cuando la posición fue igual a una de las ubicaciones de las vallas,
la ecuación para la fuerza neta fue modificada tal como se describe en la
Ecuación 2. Gambetta estimó que la zancada en la carrera con vallas, la
distancia entre un apoyo y el despegue, era de entre 3.15 y 3.50 m (Brüggemann
and Glad, 1988). En este modelo utilizamos un promedio de estos dos valores:
3.33 metros. Para cada apoyo, se registraron el tiempo y la velocidad de manera
tal que se pudieran comparar con los tiempos parciales obtenidos en las
competiciones.
Para determinar los valores apropiados de los coeficientes del modelo, se desarrollo un código en MATLAB, para repetir la carrera hasta 3000 veces, incrementando cada uno de los 5 coeficientes en (1). Luego de determinar el modelo para cada carrera, se determinó el error de la siguiente manera: en cada apoyo, se determinó la diferencia absoluta entre el tiempo observado y el producido por el modelo. Luego de esto, se calculó el promedio de esta diferencia en diez tiempos de apoyo. Se tomó el error del modelo como esta desviación promedio. Luego de esto se obtuvieron los coeficientes que produjeran el mínimo error del modelo.
Si se hallaba que uno de los valores los coeficientes se encontraba en alguno de los extremos del rango en el cual se lo había hecho variar, entonces se volvía a correr le modelo con un nuevo rango de valores. Nosotros asumimos que cuando el coeficiente exhibe un valor límite, es un indicador de se está minimizando el error para los valores en esa dirección, pero puede evitarse imponiendo un rango arbitrario. El modelo se hace correr hasta que se halla el conjunto de coeficientes que caiga dentro de sus respectivos rangos.
Característicamente, más de un conjunto de coeficientes podría producir el mismo error. Para los datos presentados aquí, nunca hubo más de cinco instancias con el mínimo error, pero una prueba resultó en más de cuarenta. Se calcularon los coeficientes asociados con el mínimo error. Estos valores fueron utilizados para recalcular el error del modelo de la misma manera descrita previamente, pero en base a un tiempo de apoyo de 0.01 segundo. Se asumió que la estimación inicial, a través de un tiempo de apoyo de 0.05 s, en general permitió un ajuste cerrado, lo cual pudo mejorarse por la variación adicional de los coeficientes.
Hemos hallado que, inicialmente, el error mínimo del modelo era de 0.015 a 0.020 s, lo cual fue ampliado a un error en el rango de 0.011 a 0.022 luego de reducir el tamaño de la zancada. En otras palabras, en ciertas oportunidades el ajuste para un tiempo de apoyo de 0.05 fue bueno respecto de la precisión pero en otras ocasiones no fue así.
El conjunto de coeficientes que produjeron el menor error utilizando el tiempo de 0.01 fue reevaluado una última vez para alcanzar una minimización adicional del error. En esta ocasión, el foco de la variación en los valores de los coeficientes fue menor. Por ejemplo, la estimación inicial para f0 pudo haber estado en el rango de 4.5 y 5.4 en incrementos de 0.1 y dar un valor de 5.0. En este caso, la estimación final podría haber tenido lugar en un menor rango que fuera de 4.96 a 5.04 en incrementos de 0.02. El resultado fue que el error del modelo estuvo en el rango de desviación de 0.010 a 0.18 s de los datos presentados.
Los valores de los coeficientes entre las diferentes carreras tendieron a ser bastante similares. De hecho, para las tres carreras presentadas aquí, toda la variación en los valores de los coeficientes se encuentra dentro de las cinco estimaciones iniciales del incremento tal como se describió previamente. Además, las pruebas realizadas con los datos de las carreras con vallas produjeron un valor de α de ~ 0.38 que fue tan consistente que se tomo como valor fijo para los resultados presentados aquí. Este procedimiento concuerda con la interpretación presentada pro Mureika (2001) de que α es una constante fisiológica y como tal no debería cambiar en gran medida de carrera a carrera.
La consideración de la consistencia de los resultados derivó en una reducción de la estimación inicial de los rangos alrededor de lo que se consideran valores esperados. Mientras que el resultado, en cierto sentido, se debió a la preselección de los coeficientes para el modelo (especialmente cuando se ha mostrado que diferentes conjuntos de coeficientes pueden producir el mismo error), las similitudes en el rendimiento de carrera al más alto nivel de competición nos permitió entender este resultado. A cualquier tasa, los valores de los coeficientes tienen poco significado inherente, excepto quizás en comparación de atletas individuales. El verdadero interés del modelo radica en que provee una herramienta para estudiar los efectos de la variación en la fuerza de arrastre.
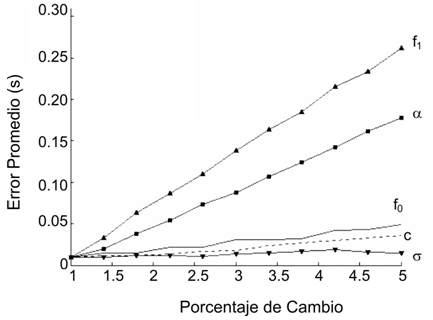
Figura 1. Cambio en la desviación promedio observada a partir de los
tiempos en la carrera de 110 m con vallas en donde se realizó la variación de
cada uno de los cinco coeficientes del modelo.
En el presente estudio también hemos investigado la sensibilidad del modelo a los valores de los coeficientes. A partir de los valores aceptados para la primera carrera de Greg Foster en el Campeonato Mundial de Atletismo de 1987 (Brüggemann and Susanka, 1988), cada coeficiente se incrementó hasta el 10% de su valor origina, manteniendo los otros constantes. El cambio resultante en el error del promedio se presenta en la Figura 1. Para los cambios en f0, c, y σ, el error del modelo fue menor que 0.05 s. Los efectos de los cambios en f1 y α son más pronunciados, con cambios en el error de 0.26 y 0.18 s respectivamente. Estos hechos fueron tenidos en cuenta para realizar las modificaciones finales de los rangos de estimación, ya que se esperaba que los cambios en un coeficiente en relación con otro pudiera desempeñar un rol más significativo en la reducción del error global.
RESULTADOS Y DISCUSION
Resultado del Modelo
Brüggemann and Susanka (1988) registraron los tiempos de los apoyos en tres carreras realizadas por el medallista de oro Greg Foster en el Campeonato Mundial de Atletismo de 1987. Sus tiempos parciales son presentados en la Tabla 1 conjuntamente con las aproximaciones arrojadas por el modelo. Evidentemente, el modelo tiene un rendimiento razonablemente bueno ya que arroja tiempos de los apoyos posteriores al traspaso de las vallas que son similares a la mayoría de los tiempos reales, pero a medida que se acerca el final de la carrera los tiempos se desvían de los valores observados. Otro aspecto a destacar es que, el tiempo real de carrera es de hasta 0.24 s más rápido que el producido por el modelo. La fuente de este error es una velocidad poco realista producida por el modelo luego apoyo posterior al traspaso de la última valla, para lo cual se realizaron correcciones que se discutirán más adelante. Obsérvese que para la presentación de los resultados, el error se ha calculado como la desviación solo durante el traspaso de la vallas. Este ajuste se llevó a cabo para ajustar con precisión los apoyos posteriores al traspaso de las vallas sin sacrificar el interés por obtener tiempos de carrera total ligeramente más realistas.
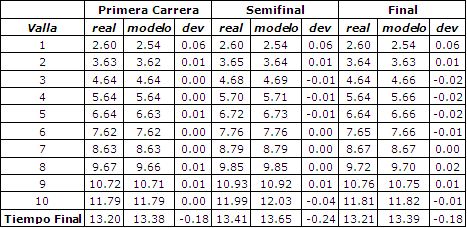
Tabla 1. Comparación entre los tiempos de contactos reales y los
arrojados por el modelo conjuntamente con las desviaciones (dev) en segundos.
Efectos del Viento y la Altura
Los coeficientes obtenidos a partir de la carrera semifinal en el Campeonato Mundial de 1987 fueron utilizados para modelar la carrera bajo cinco condiciones de viento, en un rango de -2.0 a 2.0 m/s. evidentemente, para una velocidad del viento de 2 m/s, el tiempo de carrera se reduce en 0.19 segundos. Este efecto es aproximadamente dos veces mayor que el observado cuando el modelo se utilizó para la carrera de 100 m planos.
La Figura 2 muestra gráficamente los efectos de la velocidad del viento. Con
un cambio en la velocidad del viento desde 2.0 a -2.0 m/s, la velocidad máxima
alcanzable durante la carrera cae en 3.4%, es decir desde 9.14 a 8.33 m/s.
Durante la primera parte de la carrera, la velocidad del viento no desempeña un
rol significativo, pero alrededor del décimo apoyo, los valores extremos de
velocidad del viento dan cuenta de una diferencia en la velocidad de carrera de
0.44 m/s. Por lo tanto, los efectos del arrastre sobre el atleta se acumulan a
través de la carrera. La velocidad relativa del viento es una constante en el
término que describe parcialmente la aceleración del atleta. A medida que
progresa la carrera, las diferencias en la velocidad del viento derivan en
cambios más pronunciados en el rendimiento. Debe señalarse que la gráfica ha
sido truncada considerando este efecto para ilustrar de mejor manera la
variación en la velocidad de carrera. También, se debe observar que la gráfica
muestra la relación entre los tiempos de diez apoyos y la velocidad en estos
diez tiempos específicos. Si se graficara enteramente
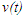 versus t se revelaría que la velocidad se reduce ligeramente al sortear
cada valla. Este hallazgo tiene un sentido intuitivo y debería quedar claro a
partir de las ecuaciones de movimiento, ya que la Ecuación 2 muestra que, en el
momento de sortear las vallas, el atleta solo enfrenta los términos resistivos.
Por una cuestión de claridad, dicho tipo de gráfica no fue utilizado.
versus t se revelaría que la velocidad se reduce ligeramente al sortear
cada valla. Este hallazgo tiene un sentido intuitivo y debería quedar claro a
partir de las ecuaciones de movimiento, ya que la Ecuación 2 muestra que, en el
momento de sortear las vallas, el atleta solo enfrenta los términos resistivos.
Por una cuestión de claridad, dicho tipo de gráfica no fue utilizado.
Los coeficientes obtenidos a partir de la carrera semifinal en el Campeonato Mundial de 1987 también fueron utilizados para modelar la carrera a cinco altitudes diferentes, desde el nivel del mar hasta los 2500 metros. Para cada cambio en la altura de 625 m, el tiempo de carrera se reduce en un promedio de 0.03 s. Obsérvese que aun con un cambio relativamente grande en la altura, el efecto sobre el tiempo de carrera es mucho menor que el provocado por la velocidad del viento.
La Figura 2b es una representación gráfica de los efectos de la densidad del aire. Claramente, los cambios en la velocidad máxima y en el tiempo de carrera son menos substanciales. Con un cambio en la altura desde 0 a 2500 m, la velocidad máxima de un atleta se incrementa solo en un 1%, es decir desde 9.00 a 9.09 m/s. como se mencionó anteriormente, los efectos combinados a través del tiempo son tales que hacia el final de la carrera hay una brecha ligeramente mayor entre las velocidades.
La Figura 3 muestra las correcciones al tiempo de llegada con el incremento en la altura para cinco velocidades del viento. La figura es una combinación de los dos análisis previos, que demuestran un incremento en el tiempo de carrera con velocidades de viento más negativas y una reducción en el tiempo de carrera con el incremento en la altitud. El modelo muestra menos efectos de la velocidad del viento con el incremento de la altura, ya que los dos factores se consideran conjuntamente en la ecuación de movimiento. Físicamente, la capacidad resistiva del aire es menor, debido a que la densidad se reduce con la altura. Interesantemente, el efecto de la altura es mucho más pronunciado cuando el viento es en contra que cuando el viento es a favor. La implicación de esto es que la altura no hace más que eliminar los efectos del viento en contra. Obsérvese que los primeros puntos de la gráfica están ligeramente desplazados debido a que estos fueron calculados para la altitud de la ciudad de Roma y no para una verdadera altura de cero metros.
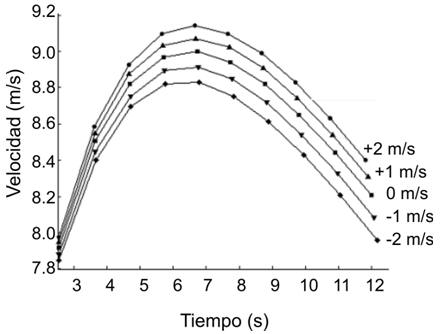
Figura 2a: velocidad del atleta durante una carrera modelada con cinco
diferentes velocidades de viento.
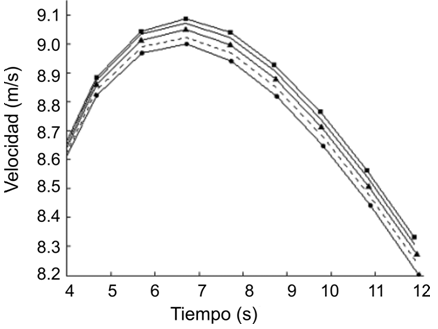
Figura 2b: Velocidad del atleta durante una carrera modelada a cinco
diferentes altitudes. Cada curva representa un incremento en la altitud de 625 m
desde 0 (la curva inferior) a 2500 m (la curva superior).
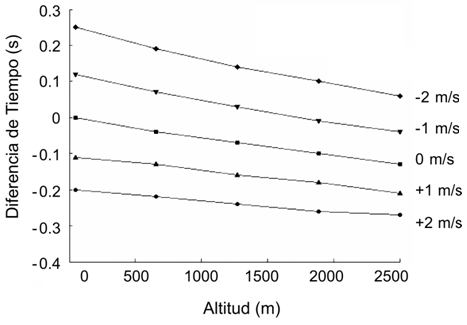
Figura 3: Cambios en el tiempo total de carrera con el incremento en la
altitud y con cinco velocidades del viento.
Aplicación
La habilidad para corregir los tiempos de carrera según los efectos de la velocidad del viento y de la altura provee una oportunidad única de reexaminar los libros de récords como si todas las carreras se hubieran corrido al nivel del mar y sin viento. En general se considera que en las carreras en donde se ha registrado una velocidad del viento de 2 m/s o mayor el atleta tiene una ayuda y por lo tanto no se incluyen en los registros oficiales. Sin embargo, la exiaminación de los récords para la carrera de 110 m con valla revelan una considerable variación en la velocidad del viento incluso entre los doce mejores tiempos oficiales (clasificados del 1 al 9) (Larsson, 2003). Los resultados presentados en las secciones previas sugieren que la corrección de esta variación podría derivar en una reestructuración significativa de los libros de récords.
Las Tablas 2 y 3 que se muestran a continuación muestran los récords oficiales y no oficiales (carreras con velocidad del viento igual o mayor a 2 m/s) para la prueba de 110 m con vallas en hombres (Larsson, 2003). Para cada carrera se realizó un modelo en el cual se incluyeron las condiciones de viento y altitud señaladas para obtener una corrección del tiempo oficial. Este método asume que hay una similitud suficiente entre los atletas como para permitir realizar las mismas correcciones como si se tratara de un corredor característico. Interesantemente, varios de los mejores tiempos entre los récords no oficiales, luego de la corrección realizada con viento cero, pasan a ser tiempos más característicos, revelando el gran efecto positivo del viento.
La Tabla 4 muestra como quedaría la reestructuración de los récords luego de realizar las correcciones correspondientes con el modelo. Obsérvese que el tiempo registrado pro Colin Jackson en Sestriere, que ese encontraba en la novena posición del ranking, ahora se encuentra en la primera posición del ranking. Este resultado es particularmente interesante, debido a que este récord en particular fue registrado a una altitud de 2065 m. La modificación revela que el viento en contra de 1.60 m/s al que enfrentó Jackson en su evento fue por lejos más significativo que la altura. Asimismo, se puede observar que el tiempo que se encontraba en primer lugar cayó al séptimo lugar por aproximadamente 0.06 s. Los resultados no oficales se han agregado a la lista reestructurada que se presenta en la Tabla 4, donde puede observarse que el tiempo de 12.87 s registrado por Roger Kingdom luego de la corrección pasó a ser de 13.15 segundos. También se puede observar que los dos tiempos que se encuentran en la octava posición, registrados por Allen Johnson en Atlanta, son carreras separadas que se encuentran en la posición dos y ocho en la Tabla 2.
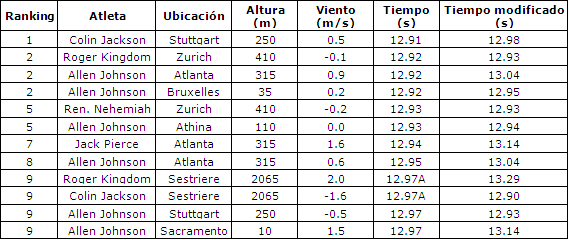
Tabla 2. Mejores tiempos en la carrera de 110 m con vallas hasta el
obtenido el 28 de abril de 2003 con las correspondientes correcciones para el
viento y la altitud. Los tiempos oficiales marcados con la letra A indican
eventos realizados en la altura (>1000 m)
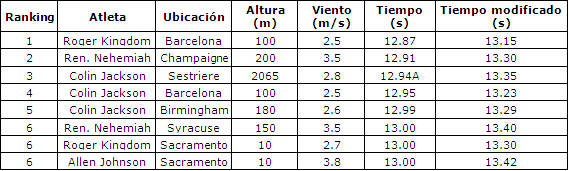
Tabla 3. Mejores tiempos no oficiales en la carrera de 110m con vallas
hasta el registrado el 28/4/2003 con las correspondientes correcciones para el
viento y la altitud. Los tiempos oficiales marcados con la letra A indican
eventos realizados en la altura (>1000 m)
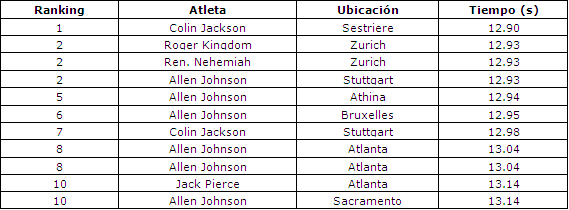
Tabla 4. Mejores diez tiempos de llegada determinados por el modelo.
Correcciones
Carrera
Aunque el modelo fue capaz de predecir tiempos parciales con una buena exactitud, los tiempos de llegada fueron siempre mayores. Parece claro que las velocidades creadas por le modelo pueden no representar las velocidades alcanzadas durante una carrera real. Incluso hablando desde un punto de vista empírico, la curva de velocidad modelada aquí decrese luego de que se alcanza el máximo, mientras que los corredores en realidad incrementan su velocidad en la porción final de la carrera. Para el Campeonato Mundial de la IAAF de 1987 (de aquí en adelante WC), cuyos datos fueron sujetos de la mayoría de nuestros análisis, no tuvimos los datos de la velocidad del viento, por lo tanto asumimos que los tiempos parciales coincidentes indicaban velocidades coincidentes.
El WC de 1997 en Atenas incluyó datos de la velocidad instantánea para los cuatro mejores corredores, por lo cual tuvimos la oportunidad de comparar estos datos con los resultados de nuestro modelo. La Figura 4 muestra que mientras que la velocidad estimada por el modelo se aproxima a la velocidad real en la mayor parte de la carrera, las dos comienzan a divergir a medida que se aproxima el final de la prueba.
Para aproximar una corrección, consideramos que el incremento observado en la velocidad hacia el final de la carrera se debió a que los corredores ya no tenían las limitaciones de carrera impuestas por las vallas. Esto es, la carrera es un esprint abierto en el cual no se aplican las consideraciones realizadas cuando los corredores deben sortear las vallas. Por lo tanto modificamos el procedimiento de modelado para reducir el valor de α luego de la última toma de contacto posterior al pasado de una valla, lo cual representa una relajación de las limitaciones fisiológicas a la longitud de zancada. Para hallar el valor de α que resultara en un ajuste de las curvas de velocidad se realizó un procedimiento de prueba y error, ingresando iguales valores de aceleración al final de la carrera. La Figura 4 muestra la velocidad corregida arrojada por el modelo, con un valor de α de 0.292 ingresado luego del décimo apoyo posterior al traspaso de una valla. El coeficiente α pudo por supuesto ajustarse para alcanzar el tiempo apropiado de carrera y pudo fácilmente ajustarse al esquema de reducción de error. Sin embargo, dicha aproximación pondría crear una aceleración poco realista. Por lo tanto sería necesario constatar el error contra la velocidad de carrera, para obtener tiempos parciales arrojados por el modelo que continúen ajustándose a los tiempos reales de carrera.
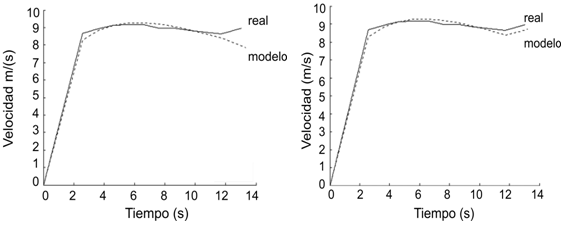
Figura 4. Comparación de las curvas de velocidad real y estimadas por el
modelo antes (izquierda) y después (derecha) de la corrección por la aceleración
de carrera.
Área de Sección Cruzada
Como se señaló en la introducción, hemos sugerido un rango de valores para el coeficiente de arrastre y para el área de sección cruzada del corredor. Asimismo, el análisis realizado aquí se basó en asumir valores para un atleta promedio. Sería posible, por supuesto, medir con precisión la talla y el peso de atletas individuales y utilizar estos valores para determinar un valor más preciso de Ad Con esto en mente, se hizo un intento por determinar los efectos de la variación den Ad sobre el tiempo de carrera. La Figura 5 muestra el efecto cuando Ad fue 10% mayor o menor. El resultado es un incremento de 0.14 s en el tiempo de carrera para el valor mínimo de Ad hasta un máximo cuando el atleta enfrenta un viento en contra de -2 m/s. Para un viento a favor de la misma magnitud, hay solo un incremento de 0.06 s en el tiempo de carrera.
También se presume que el cociente Asmall/Ad tiene cierto efecto sobre el rendimiento de carrera. La estimación del 60% se basó en la examinación de las fotos de los corredores cuando se encontraban sorteando una valla, pro no pudimos encontrar datos específicos acerca del área de sección cruzada de un corredor cuando este se encuentra sorteando una valla. Una aproximación inicial dio un cociente bajo del 40%, y la Figura 6 muestra la variación en el tiempo total de carrera para diferentes cocientes. El resultado es una desviación bastante pequeña, con un incremento en el tiempo total de carrera de 0.04 s en todo el rango de valores de Asmall.
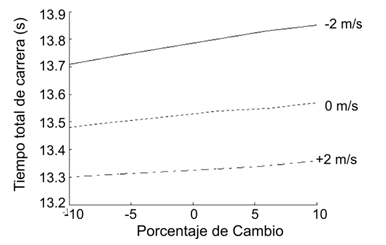
Figura 5. Cambios en el tiempo total de carrera debido a la variación en
el área de superficie de arrastre, con tres condiciones de viento diferentes.
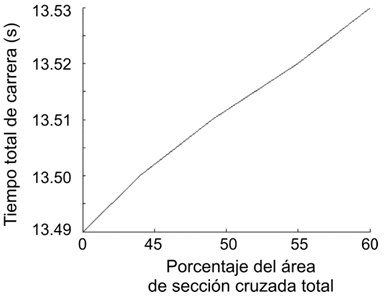
Figura 6. Cambios en el tiempo total de carrera debido a la variación en
el área de superficie de arrastre expuesta durante el traspaso de una valla.
CONCLUSIONES
Hemos mostrado que la carrera de 110 m con vallas puede ser razonablemente modelada utilizando una versión modificada de un modelo para los 100 m planos. Los tiempos de apoyos luego de traspasar una valla en la mitad de la carrera son consistentemente similares a los observados durante una carrera real, con un error promedio menor a 0.02s. Las fuentes de error hacia el final de la carrera pueden tenerse en cuenta y la disponibilidad de datos en una carrera completa podría hacer que la determinación de las correcciones apropiadas fuera más sencilla. El efecto de la velocidad del viento fue quizás el hallazgo más inesperado, ya que es aproximadamente dos veces mayor al observado en carreras de esprint sin obstáculos. Sin embargo, este efecto tiene una compensación a través del incremento en la influencia del arrastre durante el traspaso de las vallas. Una mejor determinación de los parámetros del modelo, tales como el área de arrastre o las fuerzas de propulsión podrían ayudar a determinar la validez de estas estimaciones.
Agradecimientos
JS quisiera agradecer a James Higdon por sus profundas discusiones. JRM agradece al Consejo de Investigación en Ciencias Naturales e Ingeniería de Canadá (NSERC) por el soporte financiero.
Referencias
1. Davies CTM (1980). Effects of wind assistance and resistance on the forward motion of a runner. Journal of Applied Physiology 48: 702-709
2. Dapena J, Feltner M (1987). Effects of wind and altitude on the times of 100-meter sprint races. International Journal of Sport and Biomechanics 3, 6-39
3. Keller JB (1974). Optimal velocity in a race. American Mathematical Monthly 81, 474-480
4. Linthorne N.P (1994). The effect of wind on 100-m sprint times. Journal of Applied Biomechanics 10, 110-131
5. Larsson P (2003). Track and field all time performances homepage. http://taf.sport.nu/men.htm
6. Mureika JR (2001). A realistic quasi-physical model of the 100 m dash. Canadian Journal of Physics 79, 697-713
7. Mureika, JR (2003). Modeling wind and altitude effects in the 200-m sprint. Canadian Journal of Physics 81, 895-910
8. Press, WH, Flannery, BP, Teukolsky, SA, Vetterling, WT (1993). Numerical Methods in C: The Art of Scientific Computing (2nd edition). Cambridge University Press, Cambridge
9. Ward-Smith A J (1984). Air resistance and its influence on the biomechanics and energetics of sprinting at sea level and at altitude. Journal of Biomechanics 17, 339-347
10. Ward-Smith AJ (1985). mathematical analysis of the influence of adverse and favourable winds on sprinting A. Journal of Biomechanics 18, 351-357
11. Ward-Smith, A.J (1997). A mathematical analysis of the bioenergetics of hurdling. Journal of Sport Sciences 15, 517-526
12. Ward-Smith, A.J (1999). New insights into the effect of wind assistance on sprinting performance. Journal of Sport Sciences 17, 325-334