Un Nuevo Modelo Preciso para Predecir la Frecuencia Cardíaca Máxima

El propósito de este estudio fue proponer una mejor estimación de la frecuencia cardíaca máxima (FCmáx) para hombres adultos jóvenes sanos, y también el mejor ajuste matemático para la frecuencia cardíaca (FC) versus la carga de trabajo durante un test de rampa. Veinticuatro hombres con una edad promedio de 29 ± 7 años, masa corporal de 78,4 ± 9,8 kg y un VO2 máximo de 52,9 ± 8,8 mL•kg-1•min-1 fueron sometidos a un test de ciclo-ergómetro de rampa con 10 % de su carga de trabajo máxima prevista por minuto. Se utilizaron la edad y la FC a 150 watts (FC150w) para derivar la ecuación: FC máx = 166,088 - (0,584 x edad) + (0,27 x FC150w) con r = 0,79 y Error Estándar de Estimación = 4,15 latidos•min-1. Los modelos matemáticos sigmoide (r2 = 0,62), cuadrático (r2 = 0,81) y exponencial (r2 = 0,83) no mejoraron el ajuste matemático lineal (r2 = 0.83). Los resultados indican que la ecuación podría reducir sustancialmente el error de las ecuaciones de estimación de FCmáx previas, y que no hubo ventajas en el uso de modelos matemáticos más complejos para describir la relación entre la FC y la carga de trabajo.

The purpose of this study was to propose a better estimate of maximal heart rate (HR max) for healthy young adult males, and also the best mathematical fitting for heart rate (HR) versus workload during a ramp test. Twenty-four males with a mean age of 29 ± 7 yrs, body mass of 78.4 ± 9.8 kg, and a VO2 max of 52.9 ± 8.8 mL•kg-1 •min-1 were submitted to a ramp cycle-ergometer test with 10% of their maximal predicted workload per minute. Age and HR at 150 watts (HR150w) were used to derive the equation: HR max = 166.088 - (0.584 x age) + (0.27 x HR150w) with r = 0.79 and Standard Error of Estimate = 4.15 beats•min-1 . The sigmoid (r2 = 0.62), quadratic (r2 = 0.81), and exponential (r2 = 0.83) mathematical models did not improve the linear (r2 = 0.83) mathematical fitting. The findings indicate that the equation could substantially reduce the error of the previous HRmax estimating equations, and there were no advantages in using more complex mathematical models to describe the relationship between HR and workload.

INTRODUCCIÓN

El test de esfuerzo cardiopulmonar proporciona una medición precisa no invasiva de los parámetros fisiológicos máximos (11). Sin embargo, el test debe realizarse con equipos sofisticados que requieren un técnico bien capacitado. Como resultado, la mayoría de los entrenadores han utilizado la frecuencia cardíaca (FC) para controlar la intensidad del ejercicio en el entorno de campo. La frecuencia cardíaca está relacionada positivamente con la potencia aeróbica (VO2), tal como se determina durante el test cardiopulmonar máximo (10).

Aunque algunos procedimientos y equipos pueden mejorar la seguridad del test cardiopulmonar, la medición de los parámetros fisiológicos máximos muestra algunos riesgos para la salud. Luego, en el entorno del campo, debe predecirse la frecuencia cardíaca máxima (FCmáx), en lugar de medir ese parámetro durante el esfuerzo máximo. Esta predicción de FCmáx se ha realizado mediante información que puede recogerse antes del esfuerzo (11).

La ecuación más antigua es "220 - edad". Curiosamente, no tiene un documento publicado que apoye su uso (18). La segunda ecuación más común utilizada es "208 - (0,7 × edad)". Thomas et al. (21), emplearon un estudio de meta-análisis que se agregó a un estudio transversal con una muestra grande para derivar su ecuación de predicción. La edad se usa como una sola variable independiente para ambas ecuaciones, cuyo error estándar de estimación puede ser ± 12 latidos·min-1 (20). Eso significa que, para el 95% del intervalo de confianza, hay 48 latidos·min-1 de incertidumbre. Es fácil concluir que la predicción de la FCmáx es un índice pobre para controlar la intensidad del ejercicio.

Pocos estudios han buscado el mejor ajuste matemático para la FC versus la carga de trabajo. Lima (14) informó que la función sigmoide fue la mejor para describir la relación. Conconi et al. (8) encontraron un punto de deflexión de la FC que puede explicarse por la función matemática sigmoide. Astrand et al. (2) han sugerido el uso de un ajuste lineal simple, pero reconocen que a veces se produce la deflexión de la FC.

Por lo tanto, el propósito principal de este estudio fue desarrollar una ecuación de predicción con un error menor a ± 12 latidos·min-1. El objetivo secundario fue determinar el mejor ajuste matemático para la relación entre FC y  carga de trabajo.

MÉTODOS

Sujetos

Veinticuatro hombres (edad: 29 ± 7 años, altura: 176,7 ± 5 cm y masa corporal: 78,4 ± 9,8 kg) que eran sanos y no fumadores fueron sujetos en este estudio. Catorce de los sujetos eran ciclistas amateur o triatletas y 10 participaban en programas de ejercicio físico regular. Se les dijo a los sujetos: (a) que no realizaran grandes esfuerzos (> 5 METs); (b) que eviten el alcohol y la cafeína 24 horas antes del test; y (c) que completen un cuestionario de aptitud física (22). Todos los sujetos firmaron el Consentimiento, y todos los procedimientos utilizados en este estudio fueron aprobados por el Comité de Ética Institucional.

Procedimientos Experimentales

Al comienzo, los sujetos fueron sometidos a la evaluación antropométrica. Después de esto, realizaron un test de esfuerzo progresivo máximo en un cicloergómetro con freno electromagnético (Imbrasport®, Brasil). El protocolo de esfuerzo comenzó con una etapa de 6 minutos sentados en el cicloergómetro. Luego, los sujetos pasaron por el período de calentamiento durante 4 minutos sin una carga de trabajo. Luego, se aplicó la carga de trabajo en forma de rampa, utilizando el 10% de la carga de trabajo máxima individual prevista por minuto (22). La fase de esfuerzo se completó entre 8 y 12 minutos, y la cadencia se estableció en 65 rev·min-1.

Howley's et al. (12) adoptaron los criterios de esfuerzo máximo: (a) meseta de VO2 (aumento ≤ 150 mL·min-1 o 2 mL·kg-1·min-1); (b) tasa de intercambio respiratorio (RER) ≥ 1,15; (c) 90% de la FC máxima predicha por la edad (220 - edad); (d) concepto de percepción del esfuerzo ≥19 (5); y (e) fatiga voluntaria máxima con incapacidad para soportar la cadencia del recorrido. Se empleó el valor máximo para el VO2máx y la FCmáx. Para la frecuencia cardíaca submáxima (FC150w), se utilizó la frecuencia cardíaca de 150 watts.

La ventilación y el intercambio de gases se midieron en circuito abierto (Vista Mini-CPX, Vacumed®, EEUU). Todos los sujetos usaron la máscara de silicona (V-Mask, Hans Rudolph® Inc., EEUU) conectada a una turbina bidireccional para medir el flujo de gas ("MIR" Turbine, Vacumed®, EEUU). La ventilación y el intercambio de gases se tomaron en el modo respiración-por-respiración. La frecuencia cardíaca se midió continuamente con un cardio-tacómetro (Polar RS series, Polar ElectroOy®, Finlandia). El puntaje del concepto de percepción del esfuerzo se midió al final de cada minuto empleando la escala de Borg de 6 a 20.

Análisis de los Datos

Los cálculos estadísticos se llevaron a cabo utilizando el Statistical Package for the Social Sciences® (SPSS® Inc., EUA). Se realizaron las correlaciones para elegir las mejores variables independientes para derivar el modelo matemático. La relación entre la FC y la carga de trabajo se ajustó en funciones lineales, cuadráticas, exponenciales y sigmoides. El mejor ajuste matemático se consideró como el que tiene la media cuadrática residual más baja. La significancia estadística se estableció en un nivel alfa de P ≤0,05.

RESULTADOS

La Tabla 1 presenta los datos de esfuerzo máximo. Todos los sujetos alcanzaron al menos tres de los criterios de esfuerzo máximo de Howley's et al. (12). Se observaron correlaciones significativas entre FCmáx y FC150w y entre FCmáx y edad (Tabla 2).

Tabla 1. Parámetros Fisiológicos durante el Test Cardiopulmonar (media ± DE)

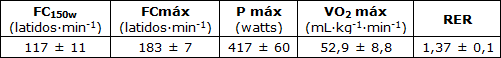
N = 24 hombres; FC150w = Frecuencia Cardíaca a 150 watts; FC máx. = Mayor Frecuencia Cardíaca en el Esfuerzo Máximo; P máx = Mayor Carga de Trabajo en el Esfuerzo Máximo; VO2máx = Potencia Aeróbica Máxima; RER = Tasa de Intercambio Respiratorio.

Tabla 2. Matriz de Correlación entre Edad, Frecuencia Cardíaca Máxima y Frecuencia Cardíaca Submáxima.

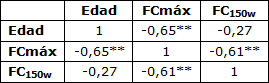
FCmáx = Frecuencia Cardíaca Máxima; FC150w = Frecuencia Cardíaca Submáxima a 150 watts; ** P≤0,01 para nivel de significancia

La FCmáx se puede predecir utilizando la siguiente fórmula:

FCmáx = 166,088 - (0,584 x edad) + (0,27 x FC150w)
r = 0,79 y EEE = 4,15

Los modelos matemáticos sigmoides (r = 0,76), cuadrático (r = 0,90) y exponencial (r = 0,91) no mejoraron el ajuste lineal (r = 0,91) para la relación FC versus carga de trabajo.

DISCUSIÓN

Mientras que algunos estudios (4,7) no encontraron diferencias entre la predicción de la FCmáx a través de "220 - edad" y las ecuaciones de Tanaka et al. (20), otros estudios (17,20) informaron una diferencia significativa entre estas ecuaciones. Además, a diferencia de nuestros datos, Tibana et al. (22) no encontraron una diferencia entre la FC medida durante el test de esfuerzo máximo y la FC estimada usando la ecuación para adultos jóvenes sanos de Tanaka et al. (20)

Astrand et al. (1-3) encontraron una gran variación individual en la relación inversamente proporcional entre la edad y la FCmáx (12,14,21,26). Además, estas ecuaciones de predicción no pueden mejorarse mediante la inclusión de una segunda variable independiente recopilada antes del test de esfuerzo, como el sexo, las actividades físicas, el tabaquismo y el índice de masa corporal (16). Por lo tanto, debido a esta muy baja precisión, Von Dobeln et al. (23) desaconsejan usar el factor edad en lugar de medir la FCmáx.

La edad explica el 42% de la varianza total de la FCmáx, y la inclusión de la FC150w podría aumentar el porcentaje de explicación al 62%. Este procedimiento podría reducir el EEE de 10 a 12 latidos·min-1, obtenido por ecuaciones de predicción previas (20), hasta 4 latidos·min-1. Este EEE está cerca de 3 latidos·min-1, que es la variación intra-individual diaria de la FCmáx durante el test de esfuerzo máximo (3).

Lima (14) informó que el 82% de la relación entre la FC y la carga de trabajo de los sujetos se ajustaba a la función matemática sigmoide. La función lineal fue mejor para el resto de los sujetos. Además, Lima (14) creía que si no se producía la meseta de la FC, entonces la función sigmoide no sería buena para ajustar matemáticamente los datos. Al igual que Bunc et al. (6), no pudimos ver una meseta de la FC y, debido a esto, la función lineal fue una mejor opción para describir la relación entre la FC y la carga de trabajo.

CONCLUSIÓN

La ecuación basada en la edad y la FC en una carga de trabajo sub-máxima ligera, propuesta en este estudio, podría reducir sustancialmente el error de estimación de la frecuencia cardíaca máxima. Además, no hubo ventajas en el empleo de modelos matemáticos más complejos para describir la relación entre la FC y la carga de trabajo de los sujetos.

AGRADECIMIENTOS

Los autores agradecen a la Fundación de Apoyo a la Investigación de Río de Janeiro (FAPERJ) por el apoyo financiero y a Fabiana Eramo por la revisión del texto.

Dirección de correo: Dr. Fernando Pompeu, 540 Carlos Chagas Avenue, Zip Code:21941-590, Rio de Janeiro, R.J., Brazil. Phone (+55 21) 3839 6826, Fax (+55 21) 3839 6801, Email: fpompeu@eefd.ufrj.br, Website: www.ladebio.com.br