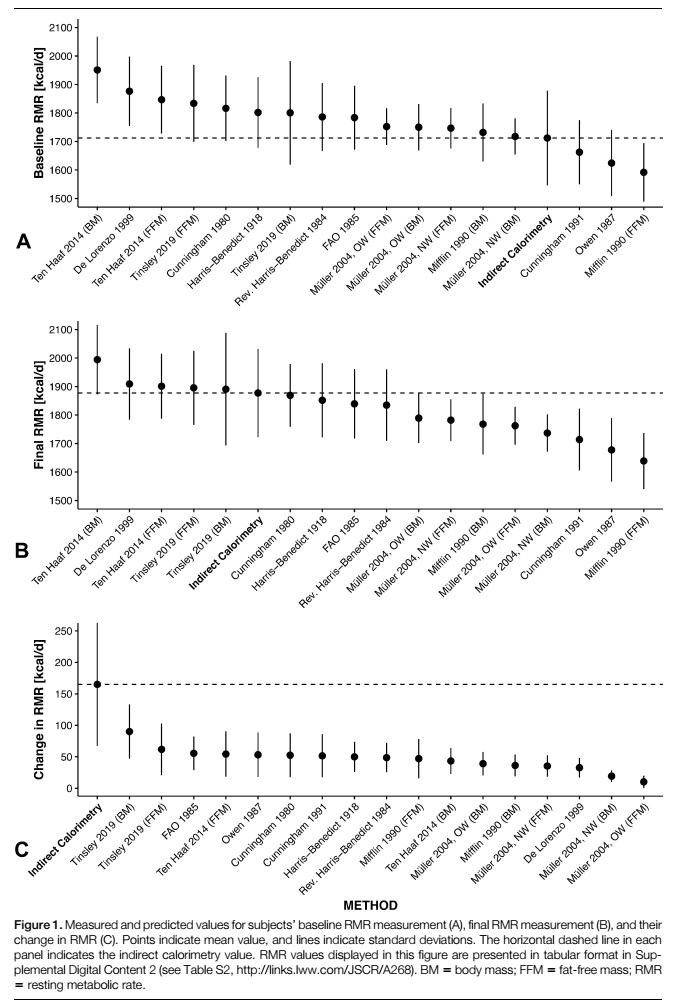
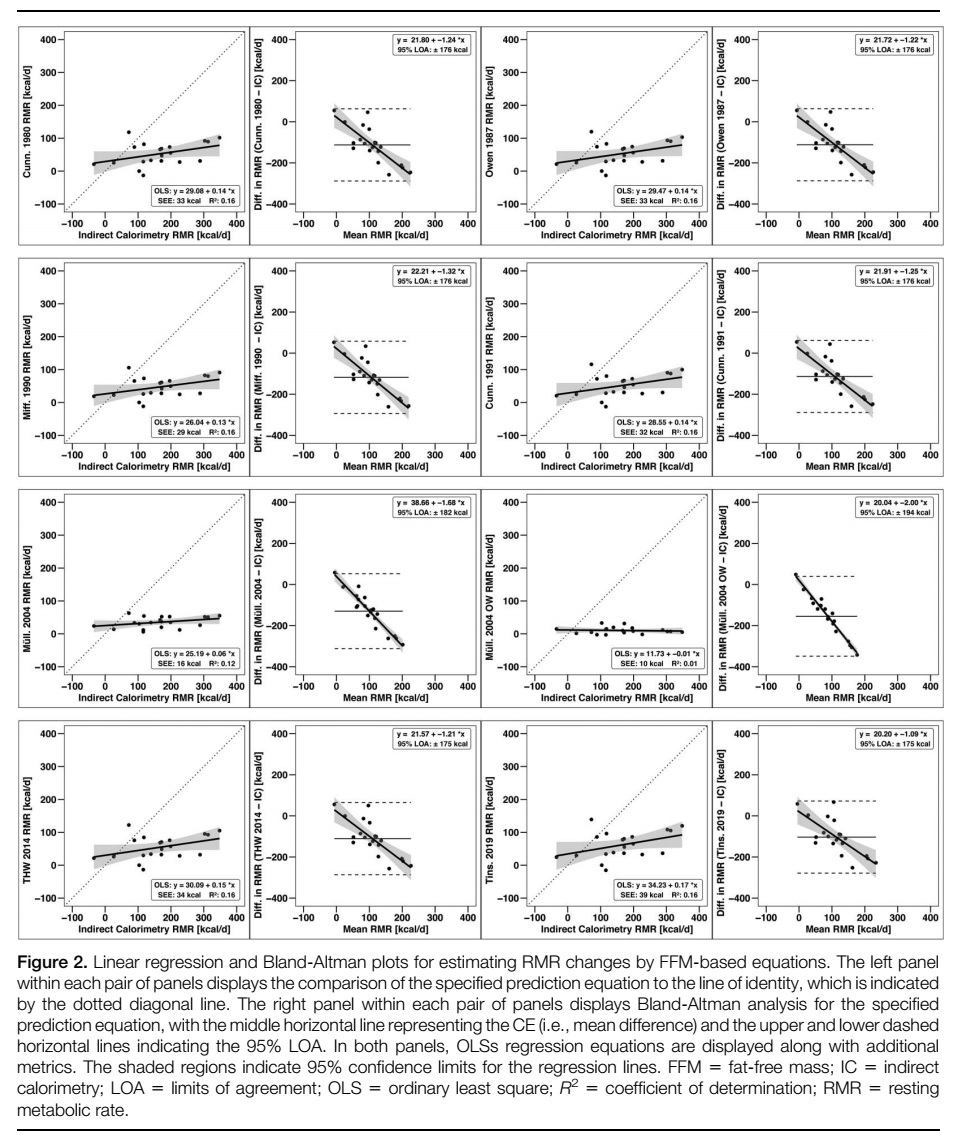
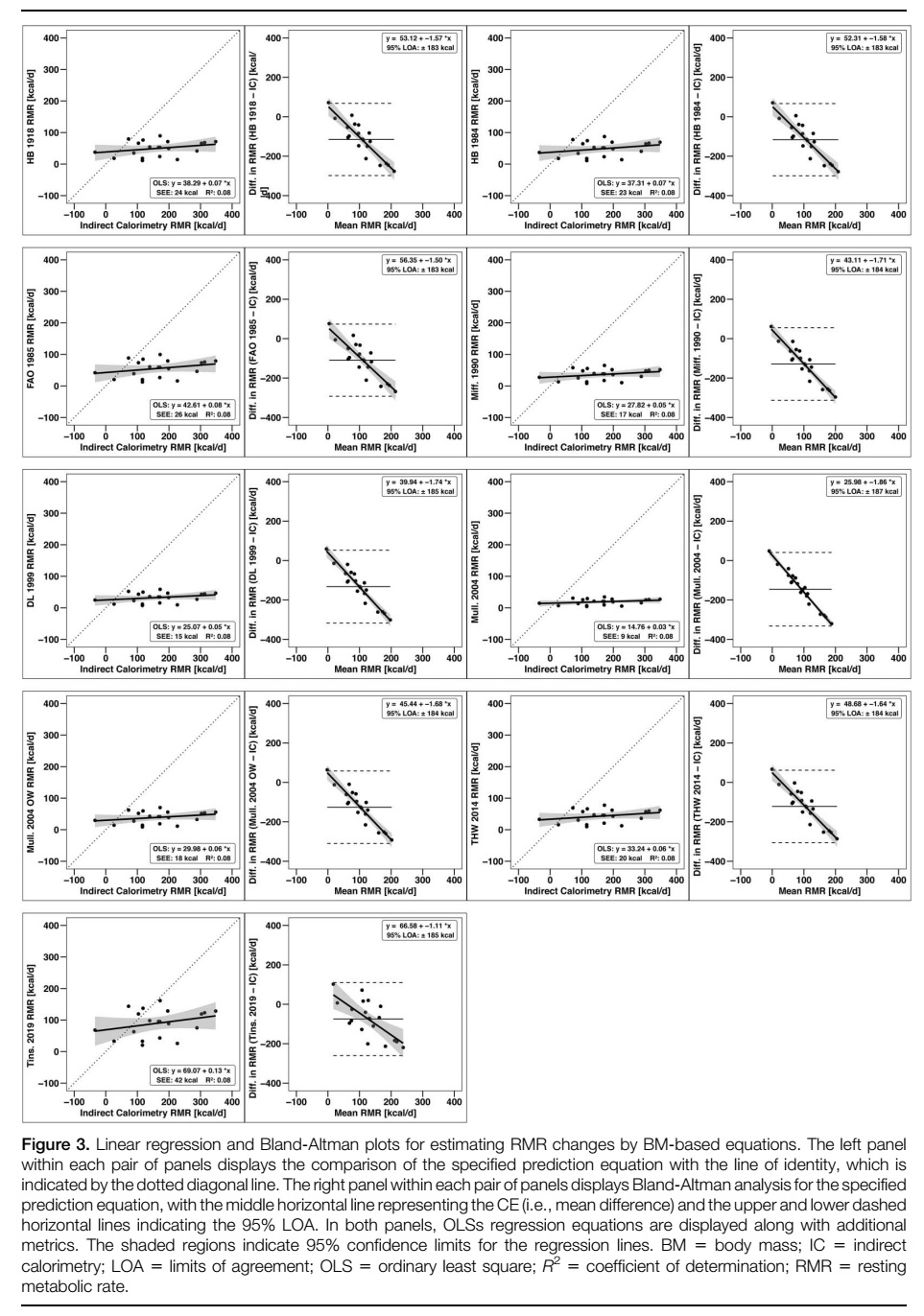
Comparación de calorimetría indirecta y ecuaciones de predicción comunes para evaluar los cambios en la tasa metabólica en reposo inducidos por el entrenamiento de la fuerza y una dieta hipercalórica

La tasa metabólica en reposo (RMR) de un individuo, que se puede definir como la energía necesaria para cumplir con las funciones corporales cruciales en reposo, suele ser el mayor contribuyente al gasto de energía (Sabounchi 2013, Xian 2015). Además, la capacidad de prescribir la ingesta energética, en base a evaluaciones de RMR precisas, es fundamental para comprender, desarrollar y ejecutar intervenciones relacionadas con el peso, tanto en el deporte como en entornos clínicos (ACSM 2016, Sabounchi 2013). La calorimetría indirecta (CI) se acepta actualmente como un método válido y confiable para medir la RMR (Jagim 2018, Pinheiro 2011). Sin embargo, el costo de los calorímetros indirectos, el tiempo necesario para completar una medición y la necesidad de personal capacitado han limitado tradicionalmente la aplicabilidad de la CI fuera de un entorno de investigación (Frankenfield 2015). Aunque algunos analizadores de CI portátiles, asequibles y fáciles de usar ya están disponibles, los profesionales de la nutrición y del ejercicio todavía utilizan a menudo ecuaciones de predicción para estimar la RMR. Estas ecuaciones se desarrollan y validan comúnmente utilizando datos de personas de una amplia gama de edades, razas, sexos, composiciones corporales y otras características (Flack 2016).

Harris y Benedict (1918) fueron pioneros en el desarrollo de ecuaciones de predicción de RMR; a saber, presentaron ecuaciones basadas en la masa corporal (BM) específicas del sexo desarrolladas a partir de una población de 239 adultos sanos hace más de un siglo. Sus ecuaciones utilizaron la altura, la masa corporal y la edad de los sujetos para predecir la RMR. Luego, Roza y Shizgal (1984) desarrollaron nuevas ecuaciones de predicción utilizando los datos del informe original de Harris y Benedict (1918) y 2 investigaciones posteriores (Benedict 1928 y 1935) realizadas en adultos que abarcaban un rango de edad más amplio. Aunque esta investigación arrojó las ecuaciones de Harris-Benedict revisadas, Roza y Shizgal (1984) informaron que los coeficientes de correlación, el error estándar de la estimación y los límites de confianza del 95% eran similares para todas las ecuaciones y finalmente sugirieron que las ecuaciones originales de Harris-Benedict (1918) eran igualmente válidas para los individuos más jóvenes y mayores.

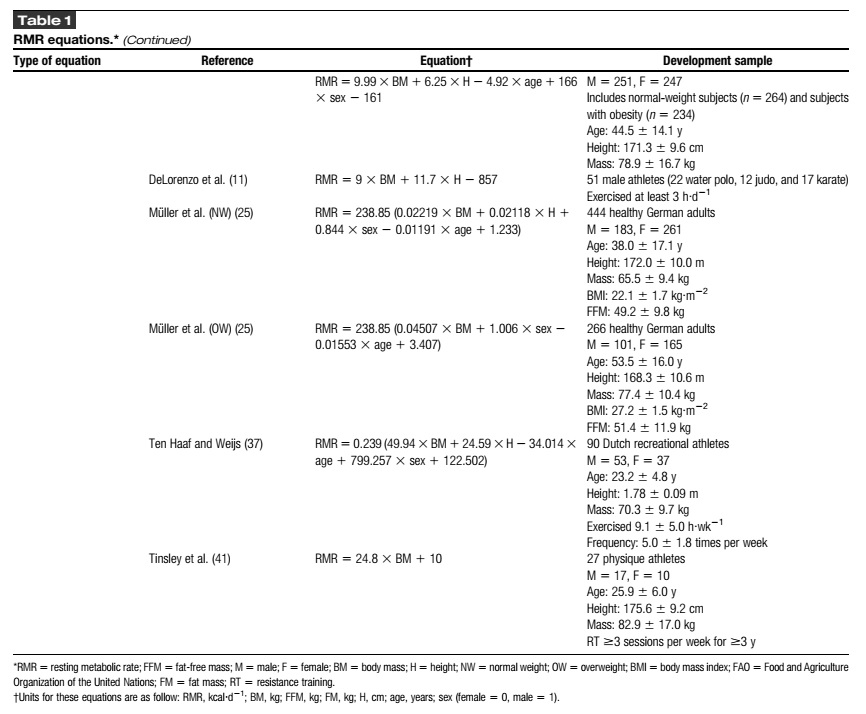
Ecuaciones adicionales de predicción basadas en la masa corporal se han originado a partir de poblaciones de adultos con peso “normal” y adultos con obesidad (Mifflin 1990, Muller 2004), atletas competitivos (De Lorenzo 1999), atletas recreativos (ten Haff 2018) e incluso atletas entrenados (Tinsley 2019). Sin embargo, las ecuaciones que no tienen en cuenta la composición corporal tienen limitaciones. Específicamente, existe evidencia de que el componente de masa libre de grasa (FFM) de un individuo puede impartir una fuerte influencia en sus requerimientos de energía (Cunningham 1991). De hecho, trabajos anteriores determinaron que la FFM representa entre el 53% y el 83% de la variabilidad en la RMR (Cunningham 1980, Flack 2016). Por lo tanto, las ecuaciones que utilizan la FFM para predecir la RMR pueden ser más precisas porque tienen en cuenta la variabilidad resultante de las diferencias en la composición corporal. Esto puede ser particularmente relevante para las poblaciones atléticas, que pueden desviarse de la relación esperada entre la BM y la composición corporal. Por ejemplo, ten Haff y Weijs (2014) determinaron que su ecuación basada en la FFM era un predictor superior de la RMR en atletas recreativos, en relación con la ecuación basada en la BM de De Lorenzo (1999). Además, este estudio destacó la importancia de considerar la población de referencia para cada ecuación de predicción cuando se aplica en la práctica. Es decir, las ecuaciones basadas en la FFM de Mifflin y cols. (1990) y Owen y cols. (1987), que se desarrollaron en la población general, se desempeñaron peor que la ecuación de De Lorenzo basada en la BM, que se desarrolló en atletas, al estimar la RMR en atletas recreativos. La ecuación de De Lorenzo se desarrolló en una muestra de atletas que incluía 22 competidores de waterpolo, 12 de judo y 17 de kárate (De Lorenzo 1999). Por lo tanto, cuando se utilizan ecuaciones de predicción, se justifica una consideración de la población objetivo porque estas ecuaciones no deben aplicarse indiscriminadamente a grupos que son diferentes a aquellos en los que se desarrollaron (Tinsley 2019).

Se han realizado evaluaciones adicionales de la precisión de la ecuación de predicción de la RMR en numerosas poblaciones, incluidos adultos sanos y adultos con obesidad (Flack 2016, Frankenfield 2005), remeros y piragüistas (Carlsohn 2011), atletas de resistencia (Thompson 1996), una variedad de atletas de deportes de equipo (Jagim 2018), y competidores físicos (Tinsley 2019). Aunque estas investigaciones transversales ofrecen una corroboración preliminar para las ecuaciones de predicción basadas en la BM y la FFM en poblaciones múltiples, no abordan una escasez notable en la literatura existente. Hasta la fecha, no se tiene conocimiento de ningún examen longitudinal que informe sobre la capacidad de estas ecuaciones de predicción para cuantificar los cambios de la RMR a lo largo del tiempo. La capacidad de identificar con precisión la variación de la RMR a lo largo del tiempo es valiosa para que los profesionales puedan prescribir los ajustes adecuados a la ingesta nutricional de un individuo en función de esos cambios. Por lo tanto, recientemente Grant M. Tinsley de la Texas Tech University (EEUU), llevó a cabo un estudio cuyo propósito fue evaluar la validez de distintas ecuaciones de predicción de uso común para rastrear los cambios de la RMR durante una intervención de nutrición hipercalórica y un programa de entrenamiento físico supervisado. En términos generales, se planteó la hipótesis de que las ecuaciones de predicción exhibirían un error significativo en relación con la CI, pero que algunas, en particular las ecuaciones basadas en la FFM, aún pueden tener utilidad para evaluar los cambios longitudinales de la RMR.

Veinte hombres entrenados en fuerza completaron el estudio. El protocolo duró 6 semanas y los sujetos se sometieron a evaluaciones de la RMR por calorimetría indirecta (CI) antes y después de la intervención para obtener valores de referencia. También se evaluaron las ecuaciones de predicción de la RMR existentes basadas en la masa corporal (BM) o la masa libre de grasa (FFM) por medio de una absorciometría de rayos X de energía dual. Se utilizaron pruebas de equivalencia para evaluar si cada ecuación de predicción demostraba equivalencia con la CI. También se realizaron pruebas de significación de hipótesis nulas y se utilizó el análisis de Bland-Altman junto con la regresión lineal para evaluar el grado de sesgo proporcional.

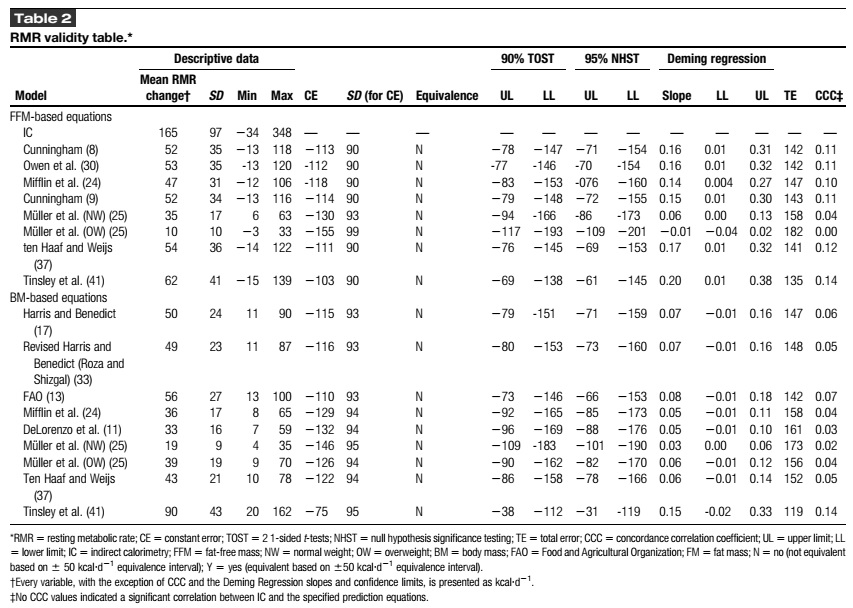
La masa corporal y la FFM aumentaron en 3.6±1.7 kg y 2.4±1.6 kg, respectivamente. La RMR por calorimetría indirecta aumentó en 165±97 kcal·d-1 y la relación RMR:FFM aumentó en 5.6±5.2%. Todas las ecuaciones de predicción subestimaron los cambios medios de RMR en relación con CI, con magnitudes que oscilaron entre 75 y 155 kcal·d-1, al mismo tiempo que mostraban niveles inaceptables de sesgo proporcional negativo. Además, ninguna ecuación demostró equivalencia con la CI. Las ecuaciones comunes de predicción de la RMR basadas en BM o en FFM no detectaron completamente el aumento en la RMR observado con el entrenamiento de fuerza más una dieta hipercalórica. En general, las ecuaciones de predicción evaluadas no son adecuadas para estimar los cambios de la RMR en el contexto de este estudio.