Efectos de la Velocidad de Carrera sobre los Costos Energéticos Metabólicos y Mecánicos de la Carrera

Este estudio evaluó la influencia de la velocidad sobre el costo metabólico y mecánico para correr una distancia dada. Corredores entrenados (n=12) realizaron dos pruebas de carrera en cintaergómetro de 8 minutos de duración a cada una de 6 velocidades (un rango de 2.33 a 4.0 m/s). Los valores de consumo de oxígeno fueron normalizados para la velocidad de carrera, proporcionando una variable de costo metabólico (MBTC, ml/kg/m). El trabajo mecánico fue calculado a partir de registros de videos digitalizados usando tres algoritmos diferentes. Los valores fueron normalizados para la velocidad de carrera, dadas las variables de costo mecánico (MTC, J/kg/m). No fue encontrado ningún cambio en el costo metabólico promedio del grupo a través de las velocidades (p=0.25). De manera contraria, el costo mecánico de la tarea disminuyó a medida que la velocidad de carrera se incrementó (p<0.001). Los tres algoritmos de trabajo mecánico resultaron en las características MTC que fueron significativamente diferentes una de la otra (p<0.001). Este estudio sugiere que el costo metabólico por distancia permanece relativamente constante a través de las velocidades de carrera, mientras que el costo mecánico por distancia disminuye a medida que aumenta la velocidad.

INTRODUCCION

Es comúnmente sostenido que el costo metabólico de la carrera a una distancia dada no es influenciado por la velocidad de carrera. Así, si uno corre a un paso lento o rápido, no tiene consecuencias al costo metabólico total para completar la distancia. La aceptación de esta asociación entre el costo metabólico por distancia y velocidad de carrera esta basada en un antiguo trabajo de Margaria et al. (1), que reporto que el costo calórico neto del nivel de carrera era de 1 kcal/kg/km (equivalente a 0.20 ml/kg/m) para velocidades que variaban de 2.5 m/s hasta 6.1 m/s para dos corredores altamente entrenados. Un trabajo posterior de Pugh (2) y Fellingham et al. (3) apoyó los resultados del grupo de Margaria. Sin embargo, otros investigadores han demostrado, tanto incrementos dependientes de la velocidad (4) y disminuciones dependientes de la velocidad (5) en el costo de oxígeno de la carrera por distancia.

Mientras que estos aspectos descriptivos identifican diferentes respuestas del costo de oxígeno por distancia para los cambios en la velocidad de carrera, los mismos no exploran los mecanismos detrás de las respuestas. Intuitivamente, parecería que el costo metabólico por distancia estaría influenciado por los mecanismos exhibidos por el corredor. Fue demostrado que el costo mecánico total se incrementa con la velocidad de carrera (6, 7) y estuvo altamente correlacionado con el costo metabólico (6). Sin embargo, ningún estudio examinó la respuesta del costo mecánico por distancia con los cambios en la velocidad de carrera, o examinó tanto el costo metabólico por distancia como el costo mecánico por distancia simultáneamente. De este modo, el propósito de esta investigación fue evaluar la influencia de la velocidad sobre los costos metabólicos y mecánicos para correr una distancia dada.

METODOS

Características de los Sujetos

20 corredores (edad 29±5 años; talla 179±7 cm; masa corporal 72±9 kg) sirvieron como sujetos para el estudio. Todos los sujetos eran corredores de distancia entrenados y exhibían un VO₂ máx. 62.4±5.0 ml/kg/min y un VO₂ en el umbral ventilatorio (VO₂VT) de 52±4.0 ml/kg/min (82.9±2.7 % del VO₂ máx.). El tiempo de carrera en el momento del estudio para los 10 km para los sujetos era de entre 29:30 a 36:02 minutos: segundos. Antes de su participación, todos los sujetos fueron verbalmente informados acerca de la naturaleza del estudio y cada uno firmo un documento de informe de consentimiento que fue aprobado por el Comité de Revisión Institucional.

Adaptación a la Cintaergómetro/ Máxima Captación de Oxígeno/ Umbral Ventilatorio

En su visita inicial al laboratorio, se les pidió a los sujetos que realizaran una sesión de adaptación en la cintaergómetro que iba dirigida a reducir la variabilidad zancada a zancada en los corredores de campo experimentados, los cuales no tenían experiencia en la cintaergómetro (8). La siguiente visita al laboratorio de los sujetos fue para las mediciones del VO₂ máx. y para la determinación del umbral ventilatorio. Durante esta evaluación y en las evaluaciones submáximas subsecuentes, el consumo de oxígeno fue medido por medio de espirometría de circuito abierto usando un sistema de medición metabólica Sensormedics 2900 (Sensormedics Corporation, Yorba Linda, CA). Antes de cada evaluación, los analizadores de gases de la carta metabólica fueron calibrados usando preparados de gases comerciales certificados y el medidor de flujo de masa fue calibrado con un volumen de gas conocido.

El protocolo de VO₂ máx. consistió de etapas de 1 minuto y comenzaba a una velocidad de 2.67 m/s y graduación de 0%. La velocidad fue incrementada en 0.22 m/s por etapa hasta que era alcanzada una velocidad de 4.0 m/s. Todas las etapas hasta e incluyendo la primera etapa a 4.0 m/s fueron corridas en un mismo nivel de la cintaergómetro. Después del primer minuto a 4.0 m/s, la velocidad fue mantenida constante y la graduación fue incrementada en 1.0% por minuto hasta que el sujeto alcanzara la fatiga volitiba.

El consecución del VO₂ máx. fue confirmada a través del alcance dos de los siguientes criterios: a) un incremento en la tasa de trabajo sin un incremento concomitante en el consumo de oxígeno, b) un índice de intercambio respiratorio (RER) que exceda 1.1, y c) una frecuencia cardiaca dentro del 10% del máximo predicho para la edad. El umbral ventilatorio fue definido como el punto en el cual el equivalente ventilatorio para el oxígeno se incrementaba sin un incremento concomitante en el equivalente ventilatorio para el dióxido de carbono (9).

Sesiones de Economía Submáximas

De 7 a 10 días luego de la evaluación de VO₂ máx., los sujetos completaron la primera de las dos sesiones de economía de carrera. Durante las sesiones, el VO₂ en estado estable fue medido a seis velocidades de carrera (2.33, 2.67, 3.00, 3.33, 3.67 y 4.00 m/s) completadas en el orden de evaluación usando un protocolo discontinuo. Cada carrera tuvo 8 min de duración y fueron proporcionados períodos de descanso de 10 min entre las carreras sucesivas. Los valores de consumo de oxígeno de los 5 min finales de carrera a cada velocidad fueron evaluados para estabilidad por medio de análisis de regresión. Un modelo lineal se ajustaba mejor a los datos y ningún sujeto exhibió una pendiente de regresión positiva o negativa entre los minutos 4 y 8 de carrera a cada velocidad. De este modo, el promedio de los valores de VO₂ de los 5 min finales fue usado como el VO₂ para cada velocidad. Un VO₂ de ejercicio fue luego calculado sustrayendo el VO₂ promedio determinado a partir de los 5 min finales de la medición en reposo del VO₂ promedio medido en ejercicio. La variable metabólica principal de interés en el presente estudio fue el VO₂ de la carrera submáxima normalizado para la distancia recorrida. Por medio de la división del VO₂ en estado estable por la velocidad de carrera, fue logrado un valor de costo metabólico por unidad de distancia. El valor fue llamado el costo metabólico de la tarea (MBTC) y fue expresado en mililitros de oxígeno por kilogramo de masa corporal por metro de distancia recorrida (ml/kg/m). Esto permitió comparaciones de economía de carrera a través del rango de velocidades evaluadas.

Fueron impuestos controles sobre los factores que ha sido demostrado que incrementan la variación intraindividual en la economía de carrera durante las carreras submáximas. Los siguientes fueron los controles impuestos: a) En un día separado de las sesiones de economía submáxima, los sujetos corrireron 45 min en la cintaergómetro para la adaptación a la misma (8), b) las carreras de economía fueron realizadas en duplicado a través de dos días de evaluación, c) los sujetos realizaron las evaluaciones a la misma hora del día, y d) fue usado el mismo calzado para cada evaluación (8, 10, 11).

Procedimientos Experimentales- Mecánicos

Registro de Video

La variable mecánica de interés en este estudio fue la potencia mecánica total del cuerpo, normalizada para la masa corporal y la distancia recorrida. Por medio de la normalización de la potencia mecánica en este modo, las comparaciones del costo mecánico podrían ser hechas a través de las velocidades, en base a la distancia recorrida por unidad. La variable de costo mecánico fue denominada costo mecánico de la tarea (MTC) y fue expresada en joules por kilogramo de masa corporal por metro de distancia recorrida (J/kg/m).

La potencia mecánica total del cuerpo fue determinada a partir de un análisis de energía por segmentos basado en cinemática. Para seguir el desplazamiento de los segmentos y subsecuentemente calcular las energías por segmentos fueron usadas técnicas de dos dimensiones (2D) para los análisis de video. Dos cámaras de video fueron usadas para filmar a los sujetos en los lados derecho e izquierdo. La cámara operó a 60 Hertz (Hz) y estaba sincronizada a la imagen más cercana con un evento identificatorio. La claridad de la imagen fue mejorada con el uso de un obturador electrónico con un tiempo de 0.004 segundos. Para cada carrera de economía, fue obtenido un video de registro de 15 s durante el minuto cinco.

Antes de cada sesión, fueron marcados los puntos extremos de los segmentos del cuerpo estimados, por ello creando modelos de 7 segmentos para cada lado del cuerpo. Subsecuentemente, los resultados digitalizados de los registros de video del lado derecho e izquierdo fueron unidos, resultado en un modelo de 12 segmentos que fue usado para representar el cuerpo. Las características inerciales de los segmentos fueron estimadas empleando datos de parámetros de segmentos corporales de Dempster (12).

Análisis de Video

Dos zancadas fueron digitalizadas por cada sujeto en cada velocidad de carrera. Los análisis de los registros de video fueron llevados a cabo usando el Peak Performance Video Analisis System, Sistema de Análisis de Video de Alto Rendimiento (Peak Performance Technologies Inc., Englewood, CO). Los datos coordinados fueron igualados usando un recursivo Butterworth de cuarto orden, filtro digital de paso bajo. Las frecuencias de corte para cada segmento en la dirección horizontal y vertical fueron determinadas individualmente usando el método de análisis residual de Wells y Winter (13). Las frecuencias de corte en la dirección horizontal variaron desde una frecuencia baja de aproximadamente 3 Hz en la cabeza y el cuello hasta una frecuencia alta como 8 Hz en el pie. En la dirección vertical, las frecuencias de corte variaron desde 5 a 7 Hz en todos los puntos.

Cálculos de Energía

El costo mecánico fue determinado a partir de la energía mecánica y el trabajo de todo el cuerpo. El trabajo mecánico (W, Joules) y la potencia (P, Watts) fueron calculados a partir de la suma de los cambios de los niveles de energía potencial y cinética de los segmentos a través del tiempo requerido para un ciclo de carrera. La transferencia de energía entre los segmentos de cuerpo influencia el costo mecánico. La magnitud de las energías potencial y cinética de los segmentos varía dependiendo del grado al cual se les permite a las energías cambiar dentro de un segmento y/o transferirse de un segmento a otro. Si la transferencia de energía dentro de un segmento y entre segmentos es permitida, el trabajo total va a ser menor ya que va a haber un menor cambio del nivel de energía. Subsecuentemente, el trabajo mecánico de todo el cuerpo va a ser menor, ya que el mismo es calculado a partir de los cambios de la curva de energía de todo el cuerpo. La Figura 1 muestra una curva característica de la energía de todo el cuerpo.

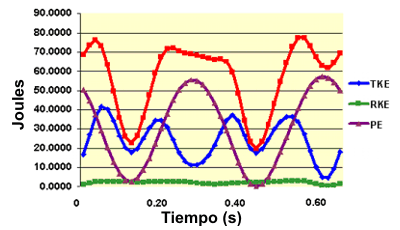
Figura 1. Curva de energía representativa.

En esta investigación fueron usados tres algoritmos separados para los cálculos de trabajo y potencia: a) el enfoque de no transferencia de Norman et al. (14), b) el enfoque de no transferencia entre segmentos de Pierrynowski et al. (15), y c) el enfoque de transferencia total de Winter (16). Para todos los algoritmos, el enfoque básico implico la determinación de la energía potencial instantánea de cada segmento (PE), de la energía cinética translacional (TKE), y de la energía cinética rotacional (RKE) a través de todo un ciclo de carrera. Los componentes de la energía fueron definidos como sigue:

PE = mgh, TKE= ½ mv², RKE= ½ Iδ²

Donde m= masa del segmento, g= aceleración debido a la gravedad, h= altura vertical arriba de un dato arbitrario, v= velocidad translacional del centro de gravedad de segmento, I= momento de inercia del segmento con respecto al centro de gravedad y δ= velocidad angular del segmento. Cada algoritmo fue diferente en la manera en la cual los cambios en el nivel de energía de los segmentos eran sumados, y de este modo, únicos en el grado de transferencia de energía permitido.

Para el algoritmo de trabajo de no transferencia (NTW), los cambios absolutos de las energías instantáneas de cada segmento fueron calculados y sumados a través de todos los segmentos (i) y todos los cuadros de video (j). Matemáticamente la ecuación usada fue:

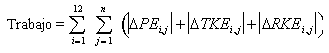
Para el algoritmo de trabajo de no transferencia (NBTW), fue calculada la energía instantánea total de cada segmento, luego los cambios absolutos de la curva de energía para cada segmento fueron sumados a través del ciclo de carrera. La suma posterior a través de los 12 segmentos en el modelo resultó en el valor NBTW. Las ecuaciones matemáticas empleadas fueron:

E_i= m_i gh_i + ½ m_i v_i² + ½ I_i w_i²

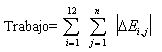
La transferencia completa de las formas de energía dentro de un segmento y entre todos los segmentos fue proporcionada en el algoritmo de trabajo de transferencia total (TTW). En el enfoque TTW, la suma de las energías instantáneas de los segmentos fue obtenida proporcionando una curva de energía de todo el cuerpo. La suma de los cambios absolutos en la curva a través del ciclo de carrera resultó en el valor TTW. Matemáticamente, la fórmulas fueron:

E_i= m_i gh_i + ½ m_i v_i² + ½ I_i w_i²

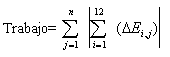
Para obtener valores de P, los valores de trabajo mecánico fueron divididos por el tiempo de zancada. Las variables MTC (J/kg/m) fueron obtenidas por medio de la normalización de P para la masa corporal y la velocidad de carrera.

Análisis Estadísticos

Para la variable MBTC, las diferencias en las medias entre la primera y la segunda sesión de carrera submáxima fueron evaluadas usando procedimientos de análisis de varianza (ANOVA) separados 2 (sesiones) x 6 (velocidades) con mediciones repetidas. Los análisis no revelaron diferencias en las sesiones de carrera (p=0.86). De este modo, los datos de las dos sesiones fueron promediados y fueron realizadas regresiones simples para describir las respuestas de la variable, a través de el rango de velocidades evaluadas.

Para las variables MTC, las diferencias en las medias entre las cuatro zancadas analizadas (2 zancadas en cada una de las sesiones uno y dos) y fueron evaluadas entre los tres algoritmos a través de análisis ANOVA 3 (algoritmo) x 4 (zancadas) x 6 (velocidades), con procedimientos de mediciones repetidas. Fueron realizados análisis post-hoc Scheffe cuando fueron detectadas diferencias entre los algoritmos y/o las zancadas. Los análisis no revelaron diferencias entre las cuatro zancadas analizadas (p≥0.82). De este modo, los datos de las zancadas fueron promediados y fueron realizadas regresiones múltiples para describir la respuesta de las variables a través del rango de velocidades evaluadas. Los análisis de regresión simple también fueron realizados para evaluar la relación entre MTBC y las variables de costo mecánico de la tarea.

RESULTADOS

Los datos descriptivos promedio a partir de las evaluaciones de VO₂ máx. son proporcionados en la Tabla 1. Las respuestas promedio a las series de carrera submáxima son proporcionadas en la Tabla 2.

Para la variable MBTC, modelos simples y polinomiales fueron ajustados a los datos y los modelos lineales simples describieron mejor la relación entre el MBTC y la velocidad de carrera. La respuesta promedio del MBTC a los cambios en la velocidad es presentada en la Figura 2. No hubo una pendiente de regresión significativa para el MTBC versus la velocidad de carrera (p= 0.25). Así, el MBTC fue independiente de la velocidad, promediando 0.164±0.004 ml/kg/m. Los datos de un solo sujeto que es representativo del VO₂ y MBTC total son exhibidos en la Figura 3.

La respuesta de las variables MTC, calculadas usando los tres diferentes algoritmos, son representadas en la Figura 3. Los valores MTC calculados con los tres algoritmos difirieron significativamente (p<0.001). Sin tener en cuenta el algoritmo empleado, fue observada una pendiente de regresión significativa para el MTC versus la velocidad de carrera (p≤0.001). Usando los métodos de transferencia restringida (Sin Transferencia, NTW y Sin Transferencia entre los Segmentos, NBTW), el MTC disminuyó un 14% desde la velocidad más lenta a la más rápida, mientras que fue observado un 32% de disminución con el enfoque de transferencia completa (TTW).

Tabla 1. Resultados descriptivos promedio de la evaluación de VO₂ máx.

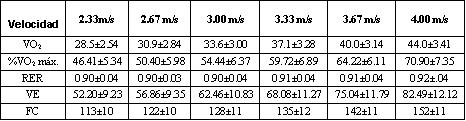
Tabla 2. Respuesta fisiológica a la carrera submáxima.

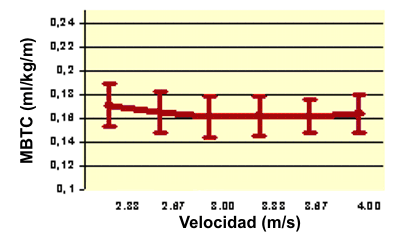
Figura 2. MBTC (ml/kg/m) versus velocidad de carrera.

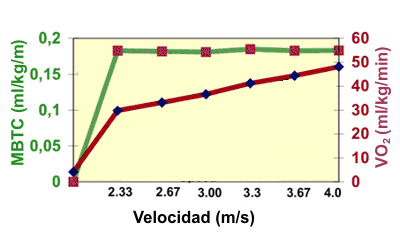
Figura 3. Respuesta del VO₂ total y del costo metabólico de la tarea.

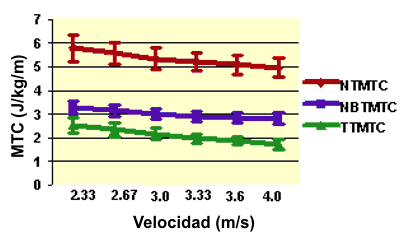
Figura 4. MTC (J/kg/m) versus velocidad de carrera.

DISCUSION

El propósito de esta investigación fue evaluar la respuesta del costo metabólico y mecánico para correr una distancia dada con los cambios en la velocidad de carrera. Desde una perspectiva metabólica, el principal hallazgo de esta investigación fue la constancia del costo metabólico por distancia (MBTC) con respecto a los cambios en la velocidad de carrera, lo cual coincide con estudios previos (1, 2, 3). Las velocidades de carrera usadas en nuestro estudio variaron de 2.33 m/s hasta 4.0 m/s, lo cual estaba dentro del rango de velocidades colectivamente examinadas en investigaciones previas (1, 2, 3). Margaria et al. (1) encontraron un costo calórico por distancia de 1 kcal/kg/km (equivalente a 0.20 ml/kg/m) para 2 sujetos, para velocidades que variaban desde 2.5 m/s hasta 6.1 m/s. Pugh (2) encontró un costo calórico constante de 0.95 kcal/kg/km para 2 sujetos y para un rango de velocidades que fue aproximadamente el mismo estudiado por Margaria et al. (1). En una investigación posterior, fue reportado un costo de 0.93 kcal/kg/km para 24 sujetos de varios niveles de aptitud física y velocidades de 2.23 y 3.13 m/s (3). Basándonos en los presentes y previos hallazgos, la independencia del MBTC y la velocidad de carrera parece ser fuerte.

Las diferencias existen, sin embargo, en la magnitud del costo metabólico por distancia entre el presente estudio y reportes previos. Mientras que no fue la intención de este estudio examinar el costo calórico, fue aplicado un equivalente calórico de 4.825 kcal/L de oxígeno a los presentes datos para permitir las comparaciones con los trabajos anteriores. Esto resultó en un costo calórico estimado de 0.79 kcal/kg/km que fue un 17 y 21% menor que los hallazgos anteriores (1, 2, 3). Las diferencias en el costo metabólico por distancia entre el presente y los estudios previos son probablemente causadas debido a diferencias en los siguientes factores: a) la economía de carrera de los sujetos; b) los controles empleados sobre factores que influencian la economía de carrera, y c) la manera en la cual fue obtenido el costo en reposo. No es sorprendente que las magnitudes de los valores MBTC de este estudio y de estudio previos mostraron una variación, dado que ha sido demostrado que el VO₂ varía de un 20 a 30% entre sujetos que corren a una velocidad particular (18) y dado que dos reportes previos emplearon solo 2 sujetos. Además, ha sido demostrado que los factores que influencian la economía de carrera (i.e., adaptación a la cintaergómetro, calzado, y variación circadiana) influencian el VO₂ submáximo en tanto como un 11% (19). A los sujetos en este estudio se les pidió que acumularan 45 min de tiempo de adaptación antes de la participación en las carreras de economía. Este tiempo fue indicado como suficiente para minimizar la variabilidad zancada a zancada en los corredores de campo experimentados, los cuales no tenían experiencia en la cintaergómetro (8). También los sujetos usaron el mismo calzado, llevaron a cabo las evaluaciones a la misma hora del día y se abstuvieron de realizar ejercicio 24 h antes de su visita al laboratorio. Ya que los efectos que tienen estos factores sobre la economía de carrera no eran conocidos por los investigadores de estudios previos (1, 2, 3, 4), es improbable que fueran hechos intentos determinados para controlar las variables. Adicionalmente, estudios pasados (1, 2, 3) fallaron en documentar los procedimientos usados para evaluar los costos en reposo. Ya que fue usado un valor neto de costo de oxígeno para calcular el costo metabólico por distancia, la variación en el costo en reposo conduciría a diferencias en la magnitud del costo neto por distancia.

Las diferencias en el costo metabólico por distancia pueden tener significancia práctica en la predicción del costo metabólico a partir de la velocidad de carrera. Actualmente, el Colegio Americano de Medicina del Deporte (American Collage of Sports Medicine) (20) usa valores de 0.2 como constante de regresión para convertir la velocidad de carrera en m/min a costo de oxígeno en ml/kg/min. Los presentes datos sugieren que el uso de 0.2 como la constante de regresión puede sobreestimar el verdadero costo de oxígeno en tanto como el 18%.

En base a los hallazgos del presente estudio y con el apoyo de estudios previos, parece que cuando los corredores son capaces de elegir libremente su velocidad de carrera, otras razones distintas que el costo metabólico para cubrir una distancia dada determinan dicha selección. El confort percibido del paso de la carrera y/o el costo mecánico pueden ser una fuerte influencia sobre la selección de la velocidad. A través de una encuesta informal de los sujetos de este estudio fue determinado que las velocidades de carrera más cómodas fueron las de 3.67 y 4.00 m/s. Los corredores indicaron que estas velocidades eran más representativas de las velocidades comunes de entrenamiento. Esta impresión fue reflejada en los resultados del MTC, donde los valores MTC fueron los menores para varias velocidades de carrera.

Sin tener en cuenta el algoritmo usado, el MTC disminuyó a medida que la velocidad de carrera se incrementó hasta 4.0 m/s. La mayor disminución en el MTC (32%) ocurrió con el algoritmo de transferencia total (TT-MTC). Con los algoritmos NT-MTC y NBT-MTC ocurrió una disminución de un 14% a través de las velocidades de carrera. Para los sujetos de esta investigación, esto sugiere un cambio benéfico en las cinemáticas de carrera a medida que la velocidad se incrementa. Además, esto sugiere que los intercambios de energía entre segmentos fueron incrementalmente más importantes a medida que la velocidad se incrementó. Este hallazgo esta apoyado por estudios previos que examinaron el costo mecánico de la carrera (6, 7). Aunque los cambios en la cinemática de la zancada y los intercambios de energía no fueron de suficiente magnitud para generar una reducción en el costo metabólico por distancia, los mismos contribuyeron a su consistencia a través del rango de velocidades evaluadas. Este cambio en la cinemática proporciona un incremento en el uso de intercambios de energía metabolicamente económicos, para ayudar en el movimiento de los miembros, lo que subsecuentemente permite el mantenimiento del costo metabólico por distancia.

En este estudio fueron empleados el algoritmo de no transferencia basado en cinemática (14), el algoritmo solo dentro de un segmento (15), y el algoritmo de transferencia completa (16). Mientras que han sido demostrados los intercambios de energía dentro de un segmento (21, 22), la extensión a la cual los intercambios ocurren entre segmentos no adyacentes es desconocida. En la presente metodología no fue tenida en cuenta la contribución del almacenamiento y utilización de la energía elástica. Los investigadores han sugerido que la energía almacenada en los componentes elásticos de los músculos contribuyen a la generación positiva de trabajo externo sin costo metabólico adicional (23). De este modo, la energía elástica podría contribuir al cambio positivo de nivel de energía. La inhabilidad de tener en cuenta la influencia de la energía elástica podría conducir a una sobreestimación del trabajo realizado. Las limitaciones del enfoque basado en cinemática para calcular el trabajo mecánico y la potencia han sido suficientemente discutidas en otras publicaciones (24, 25).

En conclusión, nuestro objetivo fue evaluar la respuesta del costo metabólico y mecánico por distancia de la carrera, a través de un rango de velocidades de carrera submáxima. Parece que el costo metabólico para correr una distancia dada es independiente de la velocidad de carrera. Sin embargo, la magnitud del costo metabólico por distancia pudo haber sido sobreestimada en reportes anteriores. Mecánicamente, los costos por distancia disminuyeron a medida que la velocidad se incrementó. La consistencia en el costo metabólico por distancia puede ser el resultado de cambios en la cinemática de carrera a medida que la velocidad se incrementa. En la locomoción humana, la constancia del costo para recorrer una distancia dada parece ser causada por alteraciones cinemáticas y cinéticas en el patrón de carrera con el incremento de la velocidad de carrera.

Agradecimientos

Los autores agradecen con gratitud a Dawn Gillis y Koichiro Fujimoto por su contribución a la recolección y reducción de los datos del experimento.

Dirección para Correspondencia

Chad Harris, Department of Kinesiology, Boise State University 1910 University Dr., Boise, ID 83725, Fax: 208-426-1894; correo electrónico: charris@boisestate.edu