Estadística Básica para los Profesionales del Entrenamiento de la Fuerza y el Acondicionamiento
Arkansas State University, Jonesboro, Arkansas.
Artículo publicado en el journal PubliCE, Volumen 0 del año 2008.
Publicado 10 de noviembre de 2008
Resumen
Palabras clave: estadística descriptiva, evaluación, fuerza y acondicionamiento
INTRODUCCION
Los profesionales dedicados al entrenamiento de la fuerza y al acondicionamiento utilizan herramientas para mejorar el rendimiento de los atletas con los que trabajan. Por ejemplo con frecuencia se prescriben ejercicios en los que se utilizan barras, mancuernas, máquinas y balones medicinales para así mejorar el rendimiento muscular. Los profesionales dedicados al entrenamiento de la fuerza y al acondicionamiento regularmente evalúan a sus atletas para valorar la efectividad del programa de entrenamiento que están llevando a cabo y para valorar el progreso de los atletas con este programa de entrenamiento. La evaluación genera información en forma numérica a lo cual nos referimos como datos. A medida que se incrementa la cantidad de datos generados, es posible que pueda perderse algo de su significado. Por lo tanto, se han desarrollado herramientas para comprender de mejor manera los datos crudos, de forma que se puedan tomar mejores decisiones acerca del entrenamiento. Estas herramientas para interpretar y resumir los datos son las estadísticas (4). El propósito de este artículo es demostrar las técnicas estadísticas básicas que los profesionales dedicados al entrenamiento de la fuerza y el acondicionamiento pueden utilizar para mejorar su capacidad profesional.
ESTADISTICA DESCRIPTIVA
La estadística descriptiva es la más simple de las técnicas estadísticas que los profesionales dedicados al entrenamiento de la fuerza y el acondicionamiento pueden utilizar. Estas técnicas son útiles para tomar una gran cantidad de datos, difíciles de interpretar, y simplemente resumir la información de manera que su interpretación sea más sencilla y por lo tanto poder tomar decisiones a partir de estos datos. La estadística descriptiva discutida en el presente artículo incluye medidas de tendencia central así como también distribuciones y valores estándar.
Tendencia Central
Una de las formas más comunes de la estadística descriptiva es conocida como medidas de tendencia central. Como el término lo indica, estos son estadísticos que describen como tienden a centrarse los datos; esto es, las medidas de tendencia central proveen un valor que representa a todos los valores. La medida más común de tendencia central es conocida como la media (2). La media es el promedio aritmético de todos los números y se calcula sumando todos los valores y luego dividiendo este valor por el número de valores. Esta medida es el “punto de equilibrio” de una distribución de valores. Aunque es muy comúnmente utilizada, la media puede no ser apropiada en todas las situaciones (5). Por ejemplo, unos pocos valores “no representativos” en un grupo de valores puede afectar adversamente la interpretación del promedio. Estos valores no representativos son conocidos como valores atípicos, y en conjunto con los demás valores darán una distribución sesgada ya que los valores atípicos afectarán la media. Los valores extremos “atraerán” a la media hacia sus valores. Una medida alternativa de tendencia central es la mediana, o simplemente el valor medio de todos los valores. Cincuenta por ciento de los valores están por encima de la mediana, y 50% de los valores están por debajo de la mediana. La mediana es la medida de tendencia central más apropiada para distribuciones sesgadas debido a que no se ve afectada por los valores extremos característicos de las distribuciones sesgadas y que afectan a la media. Considere la siguiente muestra de valores de salto vertical medidos en centímetros: 45, 46, 48, 50, 51, 51, 55, 75, 76. Los últimos dos valores serían considerados valores no representativos ya que son significativamente diferentes del resto de los valores. Ahora compare los valores de la media y la mediana de esta muestra. La suma de todos los valores, 497, dividida por el número de valores, 9, resulta en un valor medio de 55.2. La mediana se obtiene ordenando los valores de menor a mayor y luego se ubica el valor del medio. En este ejemplo, la mediana tiene un valor de 51. Ambas son medidas de tendencia central, pero como puede observarse, la media es afectada en mayor medida por los valores atípicos que la mediana. También debería señalarse que en este ejemplo, se utilizó un número impar de valores lo cual nos deja con un solo dato que se encuentra en la mitad de la distribución. Las muestras con un número par de valores resultan en un dilema, ya que en realidad hay dos valores que se encuentran en la mitad de la distribución. La solución a esto es simplemente promediar los dos datos que se encuentran a la mitad de la distribución (3). Esto con frecuencia resulta en un valor de mediana que no es realmente uno de los valores de la muestra. Otros autores han recomendado que el valor de la mediana en una muestra con un número par de datos sea el mayor de los dos valores que se encuentran en la mitad de la distribución (5).
La restante medida de tendencia central es la moda, o la puntuación que tiene mayor frecuencia (3). La moda se utilizar con datos categóricos; esto es, los datos que se clasifican en grupos. Por ejemplo, uno podría evaluar el índice de masa corporal de un grupo de personas y en base a este valor, los individuos serán divididos en grupos: grupo con “peso bajo”, grupo con “peso normal”, grupo con “sobrepeso” y “obsesos”. La moda sería la categoría con el valor que presenta la mayor frecuencia.
Variabilidad
Si bien las medidas de tendencia central son útiles para interpretar datos, solo se trata de un número que representa un conjunto de datos. La variabilidad hace referencia a las diferencias entre los valores, o como los valores se encuentran distribuidos (4). La adición de una medida de variabilidad a una medida de tendencia central nos proporciona mayor información acerca de cómo están dispersos los datos alrededor de la medida de tendencia central. Suponga que usted entrena a dos grupos que desean mejorar su aptitud física y que tienen el mismo valor promedio de aptitud física. El conocimiento de la variabilidad de la aptitud física también será una información importante debido a que puede alterar la forma en que se dictan los entrenamientos de cada grupo. De hecho, puede resultar complicado entrenar a un grupo de sujetos con una gran variabilidad en su aptitud física ya que dentro del mismo grupo puede haber sujetos con un nivel bajo de aptitud física y sujetos con un nivel muy alto de aptitud física. La medida más simple de la variabilidad de una muestra es el rango. El rango es la diferencia entre el mayor valor y el menor valor. La utilidad del rango es limitada por el hecho de que es afectado solo por dos valores (el mayor y el menor) y no dice nada acerca de los valores que se encuentran entre los dos extremos (1). Nuevamente, un único valor atípico puede afectar drásticamente el rango y derivar en una interpretación errónea. La medida de variabilidad más comúnmente utilizada es la desviación estándar. La desviación estándar es un número que indica la distancia promedio, o estándar, entre cada valor individual y la media. En términos relativos, una desviación estándar pequeña significa que todos los valores tienden a agruparse cerca de la media en comparación con una desviación estándar grande.
Por lo tanto, para describir un conjunto de datos uno debería utilizar tanto una medida de tendencia central como una medida de la variabilidad. En la mayoría de los casos lo más apropiado para los profesionales dedicados al entrenamiento de la fuerza y la resistencia es utilizar la media y la desviación estándar en forma conjunta (1). De esta manera, ambos valores son utilizados para representar muchos datos. La media y la desviación estándar proveen una “instantánea” de un gran grupo de datos, cuyo tamaño podría limitar la interpretación sin la asistencia de una herramienta estadística. Por ejemplo, considere los datos de la fuerza en 1RM en el ejercicio de press de banca obtenidos en un equipo de 30 atletas. La examinación de los datos crudos puede tornarse dificultosa sin algo de organización y/o utilizar las herramientas estadísticas de la media y la desviación estándar. Si la media de los 30 atletas fue de 150 libras y la desviación estándar fue de 10 libras, entonces el resultado podría haberse expresado como 150 ± 10 libras. De manera que dos números son suficientes para resumir el valor promedio de los datos y como los datos están dispersos alrededor de la media. Comparemos los datos de este ejemplo con los de otro equipo que tiene una media para la fuerza en 1RM en el ejercicio de press de banca de 150 libras y una desviación estándar de 20 libras (150 ± 200 libras). Esta comparación le permite al profesional dedicado al entrenamiento de la fuerza y el acondicionamiento observar que, si bien los promedios son iguales, el primer equipo tiene una menor desviación estándar, por lo que es probable que el segundo equipo tenga atletas con mayores valores de fuerza en 1RM en el ejercicio de press de banca así como también atletas con menores valores de fuerza en 1RM en el ejercicio de press de banca que el primer equipo. De esta manera puede observarse, que los datos del segundo equipo tienen una mayor dispersión o variabilidad alrededor de la media.
La Distribución Normal
Cuando se recolecta una gran cantidad de datos sobre una sola variable y se crea una gráfica de distribución de las frecuencias, esta distribución tiende a tomar una forma característica. Esta distribución es conocida como distribución normal o curva normal. Esta distribución normal tiene su mejor representación a través de la gráfica de distribución de frecuencias en donde la curva adquiere la forma de una campana (Figura 1). De hecho, esta distribución con frecuencia es denominada curva en forma de campana. La observación de la figura muestra que si se mide una variable, tal como la talla, la mayoría de los individuos estarán agrupados cerca de la media, con igual número de individuos que son extremadamente bajos y extremadamente altos.
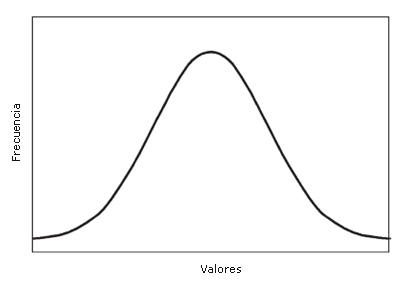
Figura 1. La distribución normal.
Esta curva simétrica es el resultado de esta relación. La simetría se encuentra alrededor del punto más alto de la curva. En una distribución normal, el punto más alto de la curvas corresponde a la media, la mediana y a la moda (1).
Además, la curva normal tiene características específicas relacionadas con las desviaciones estándar. Por definición, una desviación estándar es aproximadamente, ± 34.1% de los valores por encima y debajo de la media (5). En otras palabras, aproximadamente el 68% de los valores estarán dentro del rango que va entre más y menos una desviación estándar de la media. Suponga que un entrenador personal midió el porcentaje de grasa corporal en un gran grupo de clientes varones y con ello obtuvo una distribución normal con una media del 22% y una desviación estándar del 4%. Esto indicaría que el 68% de los individuos evaluados tendría un porcentaje de grasa en el rango del 18% (22% – 4%) al 26% (22% + 4%). Esta relación entre la desviación estándar y el porcentaje en ocasiones se denomina como la regla del 68%. Además, existen las reglas del 95% y del 99.7% para 2 y 3 desviaciones estándar, respectivamente (5). Por ejemplo, el 95% de los sujetos mencionados previamente tendría un porcentaje de grasa que iría entre el 14% (22% - 8%) y el 30% (22% + 8%), y el 99.7% de los clientes tendría un porcentaje de grasa que iría entre el 10% (22% - 12%) y el 34% (22% + 12%).
Puntuación Z
Los datos crudos pueden obtenerse utilizando diversas mediciones. A veces es difícil realizar comparaciones utilizando datos crudos. Por ejemplo, la comparación del rendimiento en el salto vertical medido en centímetros y del rendimiento en la prensa de piernas medido en libras, puede ser problemática debido a las diferencias en las unidades utilizadas para cada evaluación. Considere el siguiente ejemplo. Un individuo realiza un salto vertical de 55 cm y tiene una fuerza en 1RM en el ejercicio de prensa de piernas de 350 libras. Sería difícil realizar comparaciones útiles de los valores y determinar cómo fue el rendimiento de un individuo en relación a otros sujetos evaluados. Un método útil que permite la comparación precisa de los valores, convierte los datos crudos en un valor estándar conocido como puntuación Z. Los valores estándar se relacionan con las desviaciones estándar debido a que el valor estándar indica cuantas unidades de desviación estándar se encuentra un valor del valor medio (5). Mediante este método, cualquier dato obtenido mediante cualquier medición es convertido a una media de cero y a una desviación estándar. Los datos crudos pueden ser convertidos a puntuaciones z utilizando la siguiente ecuación:
Z = (X - M)/ DE
Donde X es el dato de interés, M es la media de la muestra y DE es la desviación estándar de la muestra. Las comparaciones precisas requieren de la media y la desviación estándar, pero un atleta podría querer saber en que test tuvo el mejor rendimiento. Teniendo la siguiente información: MVJ = 51 cm, SDVJ = 2, MLP = 3400 libras, y SDLP = 10. La realización de simples cálculos revela puntuaciones z de +2 y +1 para el salto vertical y para la prensa de piernas, respectivamente. La mayor puntuación z en el salto vertical indica un mejor rendimiento, en relación con los otros individuos evaluados, que en la prensa de piernas. Además, recuerde que una única desviación estándar por encima de la media incluye aproximadamente el 34% de las puntuaciones. Las puntuaciones z que son positivas indican valores crudos por encima de la media (50% hasta la media más 34% hasta la primera desviación estándar, lo que hace un 84%). Por lo tanto, una puntuación z de +1 indica que el valor crudo del rendimiento medido en el test fue mejor que el 84% de los sujetos evaluados. Además, una puntuación z de +2 corresponde a un valor crudo del rendimiento medido que fue mejor a aproximadamente el 97% de todos los valores (50% hasta la media más 34% de la primera desviación estándar más 13% de la segunda desviación estándar). Los valores crudos por debajo de la media producirán puntuaciones z negativas.
CONCLUSIONES
Los profesionales dedicados al entrenamiento de la fuerza y el acondicionamiento dependen de los datos numéricos para valorar el progreso de sus clientes o atletas y para valorar si los programas de entrenamiento cubren las necesidades de los atletas. La estadística descriptiva debería ser una herramienta de uso regular entre los profesionales del entrenamiento para mejorar su práctica profesional. En el presente artículo se minimizó la utilización de ecuaciones y cálculos matemáticos. En la actualidad las computadoras, a través del uso de planillas de cálculo, facilitan el registro de datos y son capaces de llevar a cabo muchos cálculos estadísticos. Con un esfuerzo mínimo, los profesionales dedicados al entrenamiento de la fuerza y el acondicionamiento pueden utilizar estas herramientas estadísticas para mejorar la evaluación de los datos obtenidos regularmente, y así maximizar los beneficios que el cliente o atleta puede obtener de los programas de entrenamiento.
Referencias
1. Baumgartner, TA, Jackson, AS, Mahar, MT, and Rowe, DA (2003). Statistical tools in evaluation. In: Measurement for Evaluation in Physical Education and Exercise Science. New York, NY: McGraw-Hill. pp. 3958
2. Harman, E, Garhammer, J, and Pandorf, C (2000). Administration, scoring, and interpretation of selected tests. In: Essentials of Strength Training and Conditioning. Baechle, TR and Earle, RW, eds. Champaign, IL: Human Kinetics. pp. 287317
3. Lomax, RG (2000). Univariate population parameters and sample statistics. In: An Introduction to Statistical Concepts for Education and Behavioral Sciences. Mahwah, NJ: Lawrence Erlbaum Associates. pp 4255
4. Sifft, JM (1990). Utilizing descriptive statistics in sport performance. Nat Strength Cond J 12: 3841
5. Vincent, WJ (2005). of central tendency. In: Statistics in Kinesiology, 3rd Edition. Champaign, IL: Human Kinetics. pp. 5277