Influencia de la Masa Corporal en el Ciclismo

El ciclismo es un deporte complejo en el cual el costo energético de un atleta está relacionado a dos fuerzas principales: la resistencia del aire cuando se viaja en terreno llano y la gravedad cuando se viaja cuesta arriba. Tanto los datos obtenidos en el túnel del viento como las mediciones fisiológicas sugieren que la resistencia del aire es proporcional a la masa corporal elevada a una potencia de 1/3. Así, los ciclistas de masa corporal grande solo presentan una resistencia aerodinámica frontal ligeramente mayor a la de los ciclistas de baja masa corporal. Si es expresada relativa a la masa corporal, la resistencia aerodinámica frontal de los ciclistas de menor masa corporal es considerablemente mayor a la de los ciclistas de masa corporal grande. La diferencia en el área frontal (costo energético) no es compensada por la ventaja de los ciclistas de baja masa corporal en el VO₂ máx. relativo (aporte de energía), debido a que el exponente de la masa para la resistencia aerodinámica (1/3) está más cercano a cero que para el VO₂ máx. (2/3). Así, los ciclistas de baja masa corporal estarían en desventaja en las pruebas contrarreloj llanas, lo cual está apoyado por los datos de campo. El costo energético del ciclismo en subida favorece ligeramente a los ciclistas de mayor masa corporal, debido a que el peso de la bicicleta representa una carga relativamente menor de lo que lo hace para un ciclista de baja masa corporal. El exponente de la masa es 0,79. Debido a que este exponente es mayor que el para el VO₂ máx., los ciclistas de baja masa corporal tienen una ventaja en la escalada, lo cual está apoyado por los datos de campo.

INTRODUCCION

Atletas de diferentes masas corporales parecen sobresalir en diferentes deportes. Un ejemplo obvio es en la carrera, donde los corredores de larga distancia exitosos tienen generalmente menor masa corporal que los miembros promedio de la población, mientras que los velocistas tienen generalmente una mayor masa corporal que el promedio.

Tales diferencias han sido estudiadas en la literatura científica para el esquí de cross-country (2, 3), la carrera (4) y el remo (12). El presente análisis se centrará en como influencia el tamaño corporal al rendimiento en el ciclismo y se realizará el siguiente enfoque. En primer lugar, será presentado el concepto de proporcionalidad, explicando como es usado para relacionar la función fisiológica con el tamaño corporal. En segundo lugar, van a ser estudiados datos experimentales concernientes a los efectos del tamaño corporal sobre las demandas de oxígeno en el ciclismo. En tercer lugar, serán estudiados resultados de eventos competitivos de ciclismo a luz de estas relaciones.

PARAMETRO DE CONVERSION A ESCALA (SCALING)

El scaling constituye el estudio acerca de cómo difieren determinados aspectos en objetos geométricamente similares. Debe recordarse, que esta aplicación a los humanos es precisa solo cuando se consideran a atletas de diferentes tamaños, pero con proporciones corporales similares.

El área es proporcional al cuadrado de las dimensiones lineales (A=L.L). Dada la densidad similar de los tejidos corporales entre los individuos de distintos tamaños, la masa es proporcional al volumen. En muchos casos, es conveniente realizar la relación usando a la masa corporal como la variable de referencia. Así, las dimensiones lineales son proporcionales a la masa corporal elevada a una potencia de 1/3, y el área es proporcional a la masa elevada a una potencia de 2/3.

Es importante señalar el efecto de los exponentes de la masa entre 0 y 1. Si un dado factor es proporcional a la masa elevada a una potencia de 1, entonces este factor es por definición directamente proporcional a la masa, y los individuos de diferente tamaño van a tener el mismo valor para este factor, si el mismo es expresado relativo a la masa corporal. Por ejemplo, la cantidad absoluta de ATP almacenado debería ser directamente proporcional a la masa corporal. Así, uno podría predecir que la potencia anaeróbica es mayor para los individuos de mayor masa corporal, pero igual entre individuos, si es expresada relativa a la masa corporal.

Si un factor tiene un exponente para la masa de 0, entonces no hay diferencia en el valor absoluto para el factor entre individuos de diferentes tamaños. Pero si este factor es expresado relativo a la masa corporal, el término sería mucho mayor para los individuos de menor masa corporal.

La mayoría de los factores fisiológicos son proporcionales con un exponente de masa menor a 1. Mientras más cercano está el exponente a 0, menor es la diferencia absoluta que existe entre los individuos, pero mayor es la diferencia relativa que existe en proporción a la masa corporal. Si se considera a dos adultos geométricamente similares que pesan 70 y 105 kg, respectivamente. El último es un 50% más pesado que el primero, pero tendría solo un 31% más de área superficial (1,72 vs. 2,25 m²). La pequeña diferencia absoluta en el área superficial se debe a que el exponente para la masa es menor a 1, específicamente 2/3. Si el área superficial es expresada en términos relativos a la masa corporal, 172 m²/70 kg vs. 2,25 m²/105 kg, entonces uno observa que los individuos con menor masa corporal tienen proporcionalmente más área superficial: 0,025 unidades vs. 0,021 unidades. Una mayor área superficial relativa tendría consecuencias fisiológicas, tales como una más rápida pérdida de calor, y tendría también un impacto sobre el rendimiento en el ciclismo, tal como será discutido luego.

ALOMETRIA

Mientras que el exponente para la masa del área superficial puede ser derivado fácilmente, resulta más complejo determinar los exponentes para la masa para la mayoría de las variables fisiológicas. Sin embargo, es posible calcular los exponentes para la masa para la mayoría de las variables a partir de datos experimentales utilizando alometría. Si una variable es proporcional a las dimensiones corporales, entonces debería producir una correlación significativa cuando es analizada en la siguiente relación:

y=a.M^b

Si los datos son graficados en coordenadas log-log, entonces el exponente de la masa se convierte en la pendiente (b) de la recta:

log (y) = log (a) + b. log (M)

De este modo, los exponentes de la masa han sido determinados para una serie de variables fisiológicas. Por ejemplo, Kleiber (8) demostró en 1932 que la tasa metabólica en reposo es proporcional a la masa corporal elevada a una potencia de 3/4. Esto expresa matemáticamente el hecho bien conocido que indica que los mamíferos más pequeños presentan un metabolismo relativo más elevado que los mamíferos más grandes, debido a que el exponente para la masa es menor a 1.

CICLISMO EN BICICLETA ERGOMETRICA

¿Hay diferencias en el costo energético del ciclismo para los atletas de diferentes tamaños?. Para contestar esta pregunta, deberíamos aislar cualquier posible influencia que podría estar presente en el ciclismo estacionario en bicicleta ergométrica de la influencia de factores adicionales experimentados en una bicicleta que se mueve.

Un reporte reciente acerca de los efectos de la masa corporal usando sujetos que no eran ciclistas, con un intervalo de masa corporal de 58-147 kg, encontró un costo de oxígeno absoluto significativamente mayor (en L/min) para los sujetos más pesados durante el ciclismo estacionario (5). La mayor tasa de trabajo estudiada fue de 132 W, y el efecto fue eliminado cuando el costo energético del ciclismo sin carga fue tenido en cuenta. Así, a bajas tasas de trabajo puede ser observado un pequeño efecto de la masa debido al esfuerzo incrementado que los sujetos con masa corporal grande deben hacer para mover sus piernas más pesadas.

En 1987, Swain et al. (14) publicaron un trabajo que estudió la influencia del tamaño corporal en el ciclismo. Diez ciclistas entrenados con una masa corporal entre 53-89 kg participaron en una serie de tests. Cuando los datos recolectados se analizaron nuevamente, durante el ciclismo en estado estable en un ergómetro Monarck, se encontró que el consumo de oxígeno de los ciclistas no dependía de la masa corporal, tal como es ilustrado en la Figura 1. Así, los ciclistas entrenados que se ejercitan a cargas de trabajo altas no exhiben un efecto de movimiento de las piernas suficientemente grande para producir una influencia general de la masa corporal sobre el costo energético durante el ciclismo estacionario.

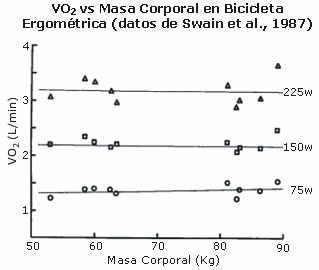
Figura 1. Consumo de oxígeno en función de la masa corporal durante el ciclismo estacionario. Datos obtenidos a partir de la ref. 14. Las pendientes de las rectas no son significativamente diferentes de cero.

CICLISMO DE RUTA

Si hay un pequeño efecto del tamaño corporal sobre el costo energético en el ciclismo estacionario, ¿que ocurre con el ciclismo de ruta?. Para contestar esto, primero se deben tener en cuenta los componentes que determinan la demanda energética en el ciclismo al aire libre – adaptado de Di-Prampero et al. (7):

costo energético = (kR.P.s) + (k_A.A.ν³) + (g.P.i.s)

Donde, k_R=coeficiente de resistencia al rodamiento, P=masa corporal combinada del ciclista y la bicicleta, s=velocidad de la bicicleta en la ruta, k_A=coeficiente de resistencia del aire, A=área superficial del ciclista, ν=velocidad de la bicicleta en el aire, g=aceleración de la grevedad; i=inclinación del camino.

El primer componente está asociado con el costo de superar la fricción entre las cubiertas y la ruta, y es directamente proporcional a la masa total del ciclista y la bicicleta. Además, el valor del coeficiente de resistencia al rodamiento varía directamente con el área superficial de la cubierta en contacto con la ruta. Así, las bicicletas de competición modernas con cubiertas finas, y con alta presión presentan una resistencia al rodamiento despreciable.

El segundo componente está asociado con el costo de empujar al ciclista y a la bicicleta a través del aire, y así es proporcional a su resistencia aerodinámica frontal combinada. Para simplificar su análisis teórico, Di-Prampero et al., asumieron que esta resistencia aerodinámica combinada era proporcional al área superficial total del ciclista. La influencia del área superficial del ciclista va a ser estudiada en mayor detalle luego. El componente de resistencia del aire es también proporcional al cubo de la velocidad, y así se convierte en el primer componente del costo energético a altas velocidades. Di-Prampero et al. expresaron a este término como ν².s (cuadrado de la velocidad en el aire multiplicada por la velocidad en la ruta). Sin embargo, debería ser ν³ (cubo de la velocidad en el aire), ya que el costo energético asociado con la resistencia del aire está determinado por medio de la multiplicación de la resistencia del aire (k_A.A.ν²) por la velocidad del ciclista a través de ese medio (ν, no s).

El componente final está relacionado al efecto gravitacional de los ascensos y descensos de cuestas, y de este modo es directamente proporcional a la masa total del ciclista y la bicicleta.

Para el ciclismo a alta velocidad en terreno llano, el principal costo energético está representado por la resistencia del aire, y debido a que la misma es proporcional al área superficial, uno asumiría que es proporcional a la masa elevada a una potencia de 2/3. Si es así, esto le daría una ventaja a los ciclistas con mayor masa corporal en términos del costo energético relativo, tal como fue predicho por primera vez por Di-Prampero et al. (7). Debido a que el exponente de la masa para el área superficial es menor a uno, los ciclistas de menor masa corporal tienen un índice de área superficial/masa corporal mayor (tal como en el ejemplo anteriormente presentado), lo cual proporciona mayor resistencia relativa al aire.

Para evaluar la predicción que indica que los ciclistas de mayor masa corporal tendrían una ventaja en el costo energético relativo, Swain et al. (14) midieron el consumo de oxígeno de 5 ciclistas de masa corporal grande y 5 de masa corporal pequeña, que pedaleaban en terreno llano. Los ciclistas de mayor masa corporal produjeron un VO₂ un 22% menor, expresado en mL..kg^-1. min^-1, en comparación con los ciclistas de menor masa corporal.

Cuando los datos volvieron a analizarse usando alometría se encontró que el exponente de la masa para el consumo de oxígeno era de solo 0,32 (produciendo la regresión un coeficiente de correlación de 0,78, p<0,01), aun menor que el valor de 2/3 esperado en base al área superficial.

En 1990, McCole et al. (10) realizaron un estudio similar acerca del costo energético del ciclismo que se centró sobre la ventaja ganada en el drafting. Fue realizado un nuevo análisis del VO₂ y el peso corporal en los datos usando alometría, usando solo los datos recolectados durante las condiciones de control (n=20), cuando el drafting no era permitido. El exponente para la masa fue 0,31 (produciendo la regresión un coeficiente de correlación de 0,52, p<0,02).

Para explicar porque el exponente de la masa presenta un valor muy por debajo de lo esperado, se debe regresar al estudio de 1987 de Swain et al. (14), en el cual fue medida el área frontal de los ciclistas en la posición en la cual pedalean en una bicicleta estacionaria en el laboratorio. Un análisis alométrico de estos datos reveló que el área frontal es proporcional a la masa elevada a una potencia de 0,55, un valor significativamente menor que el esperado de 2/3. Gran parte del tronco del ciclista está escondido en la posición de pedaleo, y aparentemente las áreas restantes que son expuestas son proporcionales con una potencia menor a 2/3.

El costo energético en el ciclismo al aire libre fue proporcional a la masa con una potencia de 0,32, lo cual implica que los sujetos pueden haber adoptado una mayor inclinación al aire libre en comparación con el laboratorio. A los sujetos se les pidió que adoptaran una posición de pedaleo similar (manos sobre la parte baja del manillar) en ambas situaciones, pero el grado de flexión del tronco no fue controlado. Otra posibilidad para considerar es la contribución de la bicicleta al área frontal total.

Las bicicletas de los ciclistas de mayor masa corporal no son mucho más grandes que las de los ciclistas de menor masa corporal. Cuando los datos de Swain et al. (14) volvieron a analizarse se encontró que los sujetos de menor masa corporal pedaleaban sobre bicicletas que pesaban el 17% de lo que pesaban ellos, mientras que para los sujetos de mayor masa corporal, esto representó solo el 12% de sus respectivos pesos (Figura 2). Así, debido a que la bicicleta implica una fracción menor de la combinación de la bicicleta y el ciclista para los ciclistas de mayor masa corporal, el área frontal total (bicicleta y ciclista) estaría desplazada a favor de los ciclistas de mayor masa corporal. La mejor forma de establecer solidamente este interrogante sería medir la resistencia aerodinámica frontal de ciclistas de diferentes tamaños en un túnel del viento.

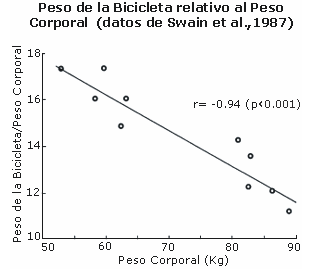
Figura 2. Peso de la bicicleta como porcentaje del peso corporal entre ciclistas entrenados. Datos obtenidos a partir de la ref. 14.

Nonweiler (11) hizo justamente esto en 1957, y cuando sus datos fueron analizados nuevamente se encontró un exponente para la masa para la resistencia aerodinámica frontal (bicicleta y ciclista) de 0,40. Mientras que hubo solamente 3 sujetos, el coeficiente de correlación fue 0,90. En 1991, Kyle (9) realizó mediciones similares en cuatro ciclistas. Tres de los cuales tenían una estructura delgada, y cuando los datos fueron analizados nuevamente se encontró un exponente de la masa para la resistencia aerodinámica frontal de 0,21, con una r igual a 0,85. El cuarto ciclista tenía una estructura robusta, lo cual altera los resultados considerablemente. Con la inclusión de este sujeto, el exponente para la masa se incrementa a 0,47, mientras que el r cae a 0,31.

Sería útil realizar evaluaciones en el túnel del viento sobre un número grande de ciclistas de diferentes tamaños, pero los datos preliminares disponibles apoyan el hallazgo a partir de los estudios de VO₂ que indican que el costo energético del ciclismo en terreno llano es proporcional a la masa elevada a una potencia de 1/3.

PRUEBAS CONTRARRELOJ

El análisis anterior indica que los ciclistas de mayor masa corporal tienen ventaja cuando se consideran esfuerzos aislados sobre terreno llano, donde la resistencia del aire es la fuerza principal que debe ser superada. Y, tradicionalmente, los mejores contrarrelojistas tienden a ser sujetos de mayor masa corporal.

En 1991, Coyle et al. analizaron el rendimiento de contrarrelojistas de elite (6).Una gráfica de sus datos brutos revela que hay una ligera tendencia (p<0,10) hacia un mejor rendimiento, i.e. menores tiempos en una prueba contrarreloj de 40 km, entre los competidores con mayor masa corporal (Figura 3).

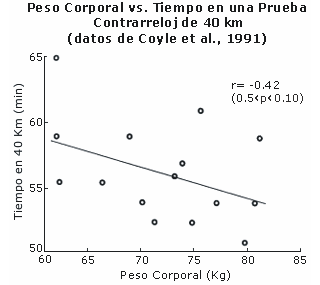
Figura 3. Rendimiento en una prueba contrarreloj de 40 km en función del peso corporal en ciclistas de elite. Datos obtenidos a partir de la ref. 6.

Coyle et al., estudiaron varios factores que podrían explicar las bases del máximo rendimiento – incluyendo aspectos como el VO₂ máx. y el umbral del lactato. La mejor variable de predicción que ellos encontraron fue la cantidad promedio de producción de potencia que el ciclista podría mantener en un test de laboratorio de 1 h. El coeficiente de correlación fue de 0,88, y cuando se eleva este valor al cuadrado, se revela que el 78% de la variación en el rendimiento en la prueba contrarreloj puede ser explicado por este único factor (6). Al expresar la producción de potencia por kilogramo de peso corporal realmente disminuye la correlación.

Para evaluar la fortaleza del exponente de la masa previamente determinado para el costo energético del ciclismo en terreno llano, estos datos han sido analizados nuevamente y son presentados en la Figura 4, la cual muestra la relación del rendimiento en una prueba contrarreloj y la producción de potencia dividida por la masa del ciclista elevada a una potencia de 0,32. La correlación es ahora mayor, con un coeficiente de correlación de 0,94, que explica el 89% de la variación en el tiempo de rendimiento.

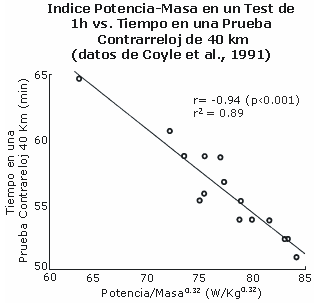
Figura 4. Rendimiento en una prueba contrarreloj de 40 km en función de la producción de potencia en 1 h dividida por la masa elevada a una potencia de 0,32. Datos obtenidos a partir de la ref. 6.

CUESTAS

En las competiciones por etapas tales como el Tour de Francia y el Tour du Pont, parece que los ciclistas promedio y los de masa corporal baja son los que terminan siendo victoriosos. ¿Cómo puede ser explicada esta observación?.

Durante las competiciones por etapas, todos pedalean en grupo, permitiendo a los ciclistas que van dentro del grupo reducir su resistencia al aire en tanto como el 40%, tal como fue determinado por McCole et al. (10). Esto efectivamente elimina la ventaja de los ciclistas de mayor masa corporal en el terreno llano.

Los ascensos montañosos, los cuales prevalecen en las carreras por etapas, constituyen enteramente otra materia. Los ciclistas disminuyen la velocidad considerablemente, reduciendo el componente de resistencia del aire, y la mayor parte del costo energético del ciclista va dirigido a vencer la fuerza de la gravedad, tal como fue descrito por la ecuación de Di-Prampero anteriormente. Este componente es directamente proporcional a la masa combinada del ciclista y la bicicleta.

Teniendo en cuenta que las bicicletas de los ciclistas con mayor masa corporal representan una menor proporción de su peso en comparación con las bicicletas de los ciclistas de menor masa corporal (12% vs. 17%, tal como se señaló antes), los ciclistas de mayor masa corporal deberían tener una ventaja relativa en el costo energético. Un nuevo análisis de los datos de un estudio acerca de ciclismo cuesta arriba en cinta rodante (15) indicó una tendencia (p<0,10) hacia un menor VO₂ relativo entre los ciclistas más pesados (Figura 5), con un exponente de la masa para el costo energético del ciclismo cuesta arriba de 0,79.

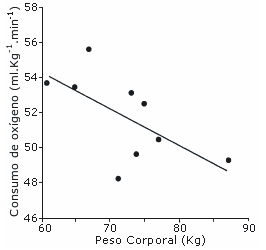
Figura 5. Consumo de oxígeno durante ciclismo cuesta arriba (pendiente de 10%) en cinta rodante a 11,3 km/h en función del peso corporal de ciclistas entrenados. Datos obtenidos a partir de la ref. 15.

Si la ventaja relativa nuevamente está a favor de los ciclistas de mayor masa corporal, ¿Por qué siempre los ciclistas de masa corporal baja parecen vencer en las cuestas?. Para contestar esto, uno también debe considerar el scaling de la potencia aeróbica máxima. Cuando se expresa en términos relativos, mL.kg^-1.min^-1, el VO₂ máx., es mayor en los atletas de resistencia de menor masa corporal en comparación con los de mayor masa corporal, tal como fue demostrado por Vaage y Hermansen en el Textbook of Work Physiology (1). El exponente de la masa del VO₂ máx. fue 2/3, el cual es el factor de 2/3 observado en el área superficial. Esta relación se mantiene para los ciclistas de elite, tal como es ilustrado en la Figura 6, la cual fue derivada a partir de datos reportados por Coyle et al. (6). En el panel inferior de la Figura 6, el VO₂ máx. fue expresado en mL.kg^-1.min^-2/3, y la pendiente de la regresión no fue estadísticamente diferente de cero.

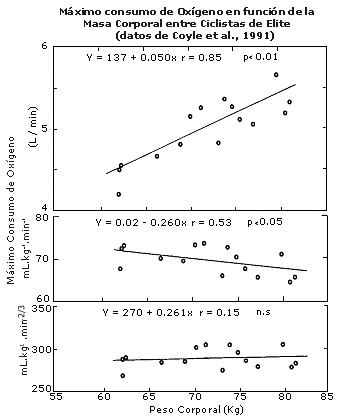
Figura 6. Máximo consumo de oxígeno en función de la masa corporal entre ciclistas de elite. Datos obtenidos a partir de la ref. 6.

Retornando a la escalada de cuestas, se debe recordar que el exponente de la masa para el costo energético era de 0,79. Aunque este número es menor que 1, es mayor que el exponente para el VO₂ máx. Así, los ciclistas de baja masa corporal deberían tener ventaja en el rendimiento durante el ascenso de cuestas, debido a que su ventaja relativa en el VO₂ máx. es mayor que la ligera desventaja en el costo energético.

Durante los descensos, cuando la fuerza debida a la gravedad y la fuerza debida a la resistencia aerodinámica del aire son significativas, los ciclistas de masa corporal elevada deberían tener ventaja, debido a que la gravedad los impulsa hacia abajo con una fuerza que es proporcional a la masa total, la cual es proporcional con un exponente de 0,79 (arriba), mientras que son expuestos a la resistencia del aire, que es proporcional con un exponente de solo 0,32. El aporte de energía en los descensos proviene de la gravedad y no del VO₂ máx.

Aunque los ciclistas más pesados descienden más rápido, no pueden recuperar el tiempo que perdieron subiendo, por lo que los ciclistas de menor masa corporal vencen en los recorridos montañosos en la mayoría de las competiciones por etapas. En un reporte reciente del Tour du Pont, fue demostrada una correlación inversa significativa entre los tiempos de finalización y la masa corporal para tres etapas montañosas (13). La etapa más montañosa, en la cual los competidores experimentaron más de 2000 m de subida en un recorrido de 158 km, produjo un coeficiente de correlación de -0,41 (con n=52, p<0,01). Así, la variación en la masa corporal explicó el 17% de la variación en los tiempos de finalización.

COMPARACIONES CON OTROS DEPORTES

Para cualquier deporte en el cual el exponente de la masa para el costo energético difiera del exponente de la masa para el aporte energético, habrá una influencia de la masa corporal en el rendimiento. El ciclismo cuesta arriba es similar a la situación de la carrera de larga distancia, en la cual ha sido demostrado por Bergh et al. (4) que el exponente para el costo de oxígeno es de 0,76. El costo de oxígeno le da a los atletas más pesados una ventaja, pero no tanto como el VO₂ máx. favorece al atleta más liviano. Así, los corredores de larga distancia exitosos en un nivel elite tienen a ser menos masivos que los individuos de tamaño promedio. Extendiendo la analogía, la carrera de velocidad es realizada a altas velocidades, en donde la resistencia del aire se convierte en un factor importante. El costo energético del esprint debería ser proporcional a la masa elevada a un exponente no mayor a 2/3. El almacenamiento de ATP debería ser proporcional a la masa. Debido a que el costo energético del esprint es proporcional a la masa con un menor exponente que la disponibilidad energética, los atletas con masa corporal mayor deberían vencer en estos eventos, en comparación con las carreras de distancia.

El deporte con la mayor similitud en scaling al ciclismo es el esquí de cross-country. Tal como en los ciclistas, los esquiadores de cross-country se desplazan a una velocidad mayor que los corredores de distancia (en relación a la resistencia del aire), y frecuentemente compiten en cuestas. En 1987, Bergh (2) publicó un excelente análisis acerca de la influencia de la masa corporal sobre el rendimiento en este deporte. El autor encontró que los esquiadores más pesados tenían una ventaja en el terreno llano y desplazándose hacia abajo, y los esquiadores más livianos tenían ventaja cuando se desplazaban hacia arriba. Fueron obtenidos resultados similares en los análisis teóricos del deporte en 1992, aunque no fueron obtenidos resultados estadísticamente significativos en los estudios de campo asociados (3). Estos resultados son cualitativamente los mismos que los del presente estudio acerca de ciclistas. Bergh concluyó que las comparaciones de la potencia aeróbica entre esquiadores de cross-country deberían ser realizadas expresando el VO₂ máx. en ml.kg^-1.min^-2/3.

CONCLUSIONES

En conclusión, los ciclistas más pesados vencen en las pruebas contrarreloj llanas, debido a que el costo energético es proporcional a la masa elevada a un factor menor que para el caso del VO₂ máx. (aporte energético), mientras que los ciclistas livianos vencen en la escalada de cuestas debido a que el costo energético es proporcional a la masa elevada a un factor mayor que para el caso del VO₂ máx.

Las comparaciones de la capacidad aeróbica de los ciclistas deberían considerar estos efectos. Para juzgar la capacidad de pedalear en terreno llano, el VO₂ máx. debería ser expresado en mL.min^-1.kg^-0,32. Para juzgar la capacidad de escalada, el VO₂ máx. debería ser expresado en mL.min^-1.kg^-0,79. Sin embargo, el valor del exponente de la masa en la escalada no está tan bien establecido como el exponente de la masa de 0,32 en el ciclismo en terreno llano.

Debe ser recordado que la masa corporal es solo un factor que afecta el rendimiento. En el análisis de la prueba contrarreloj, la producción de potencia en 1 h predijo el 78% de la variabilidad del rendimiento (6). La adición del exponente a la masa corporal mejoró la predicción en un 11% adicional. En las competiciones con etapas montañosas, la masa corporal explicó el 17% de la variación en los tiempos de finalización. Así, aproximadamente 10-20% de la variabilidad del rendimiento entre ciclistas de elite está asociada con diferencias en la masa corporal.

Agradecimientos

Agradezco a los Drs Chester. Kyle y Jim Hagberg por proporcionarme amablemente los datos brutos de sus estudios (9, 10). Quiero agradecer al Dr. Edward Coyle por incluir los datos brutos de su estudio en la publicación (6).

Dirección para el Envío de Correspondencia

David P. Swain, Ph.D., Director, Wellness Institute and Research Center, Old Dominion University, Norfolk, VA 23529-0196.