Modelo Matemático Para Predecir la Masa Corporal Magra Femenina

El propósito de este estudio fue producir un modelo matemático para predecir la masa corporal magra (MCM) a través de la evaluación del área muscular del brazo (AMB). Cuarenta y cinco mujeres jóvenes sanas (27 ± 7 años, 66,5 ± 10,4 kg) se dividieron aleatoriamente en el grupo de validación (GV, n = 30) y el grupo de validación cruzada (GC, n = 15). Los sujetos fueron sometidos a evaluaciones antropométricas e hidrométricas. El AMB se obtuvo midiendo la circunferencia del brazo derecho y el pliegue cutáneo del tríceps. El modelo derivado fue: MCM = -49,459 + (0,350 × MC) + (0,411 × A) + (0,171 × AMB); r2 = 0,91; EEE = 2,07 kg. No se encontraron diferencias significativas entre la evaluación hidrométrica y la predicción del modelo para el GC (P = 0,32; r2 = 0,91; CV = 2%). Por lo tanto, los hallazgos indican que el Modelo matemático n° 3 proporciona una evaluación similar de la MCM de la mujer como la de medida hidrométrica.

INTRODUCCIÓN

La evaluación de la composición corporal es un procedimiento clínico muy importante, así como un medio para comprender el rendimiento deportivo. La grasa corporal está negativamente asociada con varias enfermedades, bienestar, estado físico y alto nivel de rendimiento (7,9,10). La comprensión de la conexión entre la grasa corporal y la masa corporal magra (MCM) es útil para mejorar la dieta y/o el programa de ejercicios de un individuo. Sin embargo, se reconoce comúnmente que el acceso a esta información a menudo es costoso y requiere el uso de equipos de laboratorio complejos. Además, en el entorno clínico, existe la falta de una técnica precisa y práctica que sea relativamente fácil de administrar.

Como resultado, se ha convertido en algo común que los profesionales de la salud usen la relación entre la masa corporal y la estatura para evaluar la composición corporal (10). La impedancia eléctrica biológica tetrapolar (BIA) es una de las técnicas complejas utilizadas para determinar la composición corporal (1,12,14,15). En comparación con el pesaje subacuático, el método BIA tiene una buena validez y fiabilidad [r = 0,84 a 0,98; EEE = 1,31 a 5,8 kg] (5,6,11,16,18,25). Sin embargo, la técnica requiere un técnico bien entrenado, y es necesaria una preparación detallada del tema para esta evaluación (13).

Por otro lado, existen algunas evaluaciones antropométricas que son una buena opción para estudiar la composición corporal (19,20,23,25). Por ejemplo, existen varias ventajas al utilizar las áreas musculares y grasas del brazo del sujeto mediante estimaciones antropométricas (8). La circunferencia del brazo y las mediciones del pliegue de la piel del tríceps son muy precisas (17), no requieren mucho tiempo, tienen un bajo costo operativo, no requieren una preparación complicada del sujeto y no necesitan un profesional altamente capacitado. Por lo tanto, el propósito de este estudio fue desarrollar un modelo matemático simple, rápido, barato y preciso para estimar la masa corporal magra femenina joven a través del área muscular del brazo.

MÉTODOS

Sujetos

Cuarenta y cinco mujeres participaron como sujetos en este estudio. Los sujetos aparentemente estaban sanos y participaban regularmente en un programa de ejercicio físico (Tabla 1). Treinta sujetos participaron en el grupo de validación interno (GV) y 15 participaron en el grupo de validación externa (GC). Se aconsejó a cada sujeto que no realizara un gran esfuerzo (≥5 METs), que no tomara diuréticos ni que bebiera alcohol 24 horas antes de las pruebas. Las pruebas se realizaron después de un período de 4 horas post-prandial, y 30 minutos después de que los sujetos vaciaron sus vejigas (26). Todos los sujetos recibieron información sobre los procedimientos experimentales y firmaron un formulario de consentimiento informado. Los procedimientos del estudio fueron aprobados por el Comité de Ética Institucional (Registro de Aprobación del Comité Ético: CAE 09237613.1.0000.5257).

Procedimientos Experimentales

La composición corporal se evaluó mediante técnicas antropométricas e hidrométricas. El pliegue cutáneo del tríceps (17) se midió con un calibrador con 10,0 g/mm2 de presión (Lange Skinfold Caliper®, EUA). La circunferencia del brazo se midió usando una cinta métrica metálica (Samy American Medical®, Br). El mayor error en la lectura a escala se estableció en 1,0 mm para el pliegue cutáneo y la circunferencia del brazo.

La masa corporal se midió considerando 0,1 kg, y la altura considerando 0,1 cm como el error máximo en la lectura a escala (Welmy®, Br). El volumen de agua corporal se midió por impedancia eléctrica tetrapolar, con 200 - 1,500 Ohmios de resistencia, 1 Ohm de resolución, 1% de error y 800 μA y 50 kHz en intensidad y frecuencia de la corriente eléctrica, respectivamente (BIA 310e Analizador, Biodynamics®, EUA).

El área muscular del brazo (AMB) se estimó por:

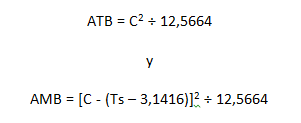
Donde: ATB = área total del brazo; AMB = área muscular del brazo, C = circunferencia del brazo derecho relajado, medido en el punto meso-humeral; y Ts = pliegue cutáneo del tríceps.

Análisis Estadísticos

Todos los cálculos estadísticos se realizaron usando un Paquete Estadístico para el software Social Sciences® (EEUU). Los datos se mostraron en media ± desviación estándar (DE). El error intra-evaluador se midió a través del error técnico de medición (ETM), o:

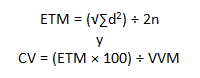
Donde: ETM = error técnico de medición; CV = coeficiente de variación en %; Σd² = suma de error cuadrada; n = tamaño de la muestra; VVM = valor de la variable media.

El intervalo de concordancia de Bland-Altman (4) se aplicó entre BIA y los resultados del modelo predictivo. El coeficiente de correlación intraclase (23) se utilizó para medir la asociación entre BIA y los valores del modelo predictivo. El error de predicción se evaluó a través del error estándar de estimación (EEE) y mediante el coeficiente de variación. El nivel de significancia se estableció en P≤0,05.

RESULTADOS

Las características antropométricas de los sujetos se presentan en la Tabla 1. El ETM intra-evaluador fue del 5% para los pliegues cutáneos y no mayor del 1% para las otras mediciones.

Tabla 1. Características Antropométricas de los Sujetos.

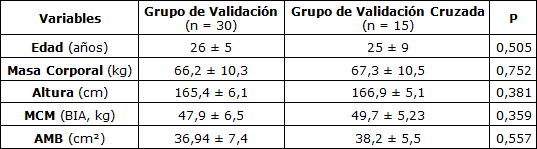
n = (Voluntarios) Número de Sujetos; GV = Grupo de Validación; GC = Grupo de Validación Cruzada; P = Significancia de Diferencia entre Grupos; MCM = Masa Corporal Magra; BIA = Impedancia Eléctrica; AMB = Área Muscular del Brazo

La matriz de correlación (Tabla 2) muestra la correlación más fuerte de la MCM con la masa corporal, seguida por la altura, la circunferencia del brazo contraído, la circunferencia del brazo relajado, el índice de masa corporal y el AMB. La Tabla 3 muestra los modelos matemáticos para predecir la MCM derivada del GV.

Tabla 2. Matriz de Coeficiente de Correlación entre Medidas Antropométricas y de Impedancia Eléctrica.

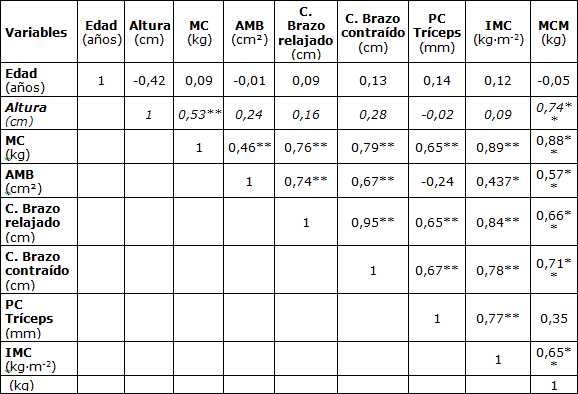
AMB = Área Muscular del Brazo; C = Circunferencia;  PC= Pliegue Cutáneo; IMC = Índice de Masa Corporal; MCM = Masa Corporal Magra; *P≤0,05; **P≤0,01 Nivel de Significancia

Tabla 3. Modelos Matemáticos para la Predicción de Masa Corporal Magra.

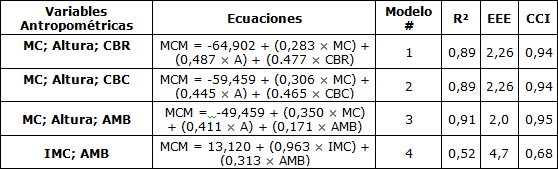
MC = Masa Corporal; AMB = Área Muscular del Brazo; A = Altura; CBR = Circunferencia del Brazo Relajado; CBC = Circunferencia del Brazo Contraído; MCM = Masa Corporal Magra; IMC = Índice de Masa Corporal; R² = Coeficiente de Determinación; EEE = Error Estándar de Estimación; CCI = Coeficiente de Correlación Intraclase

Cuando estas pruebas se aplicaron en el grupo externo (GC), no se encontraron diferencias significativas entre la MCM predicha por los modelos matemáticos y la MCM determinada por BIA. El modelo 3 explica el 91% de la variación de la MCM. La Figura 1 muestra el diagrama de dispersión y el 95% del intervalo de concordancia de Bland-Altman para la validez externa (GC).

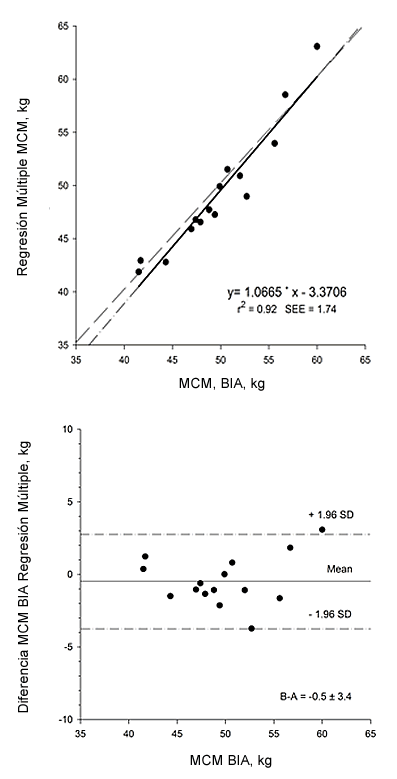
Figura 1. Regresión, Correlación e Intervalo de Concordancia de Bland-Altman entre MCM Predicha por el Modelo n° 3 y Determinada por BIA para el Grupo de Validación Cruzada.

DISCUSIÓN

La masa corporal magra se puede medir mediante la conducción eléctrica del agua corporal (3). El aparato de impedancia eléctrica biológica tetrapolar puede medir la resistencia del cuerpo contra una corriente eléctrica imperceptible. Eso es inversamente proporcional al agua corporal total. Esta masa se puede determinar porque tiene un contenido de agua muy estable. Esta técnica es confiable y tiene una excelente correlación con la densitometría, que es el método gold standard (1). Sin embargo, para una medición precisa, es necesaria una larga y metódica preparación del sujeto para evitar hiper o hipo-hidratación (3). Los autores de este estudio no han encontrado una diferencia significativa en la masa grasa entre las mediciones en dos momentos cercanos, cuando se emplean esos procedimientos de preparación (n = 30; 13,99 ± 3,96 frente a 13,78 ± 4,12%, CCI = 0,94).

En este estudio, la altura y la masa corporal tenían una fuerte correlación con la MCM (Tabla 2). Debido a esto, los autores trataron de incluir el índice de masa corporal en el modelo matemático. Sin embargo, el modelo predictivo con este índice tenía un coeficiente de determinación más bajo y un error estándar de estimación más alto. La transformación de Fisher, para la inclusión de este índice, no mostró una mejora predictiva. Además, aunque no hubo diferencias entre los modelos, se debe elegir el tercer modelo. Este modelo presenta valores predictivos más cercanos a las mediciones de BIA. Además, esta ecuación presenta ventajas porque el AMB y el área de grasa del brazo pueden medirse con buena precisión. Además, cuando estas áreas cambian, nos brindan información directa sobre la MCM y las alteraciones del compartimento graso y, también, sobre la fuerza máxima del brazo y del tronco (22).

Aunque la edad puede influir en la composición corporal (21), el presente estudio no encontró una mejora en la predicción de la MCM cuando la edad se incluyó en el modelo matemático. Se encontraron datos similares en otro estudio con sujetos masculinos (24). Esto probablemente ocurrió debido al estrecho rango de edad en ambos estudios.

CONCLUSIONES

Dado que no se encontraron diferencias significativas entre la evaluación hidrométrica y la predicción del modelo para el GC (P = 0,32; r2 = 0,92; CV = 2%), los hallazgos indican que este modelo matemático [MCM = -49,459 + (0,350 × MC) + (0,411 × A) + (0,171 × AMB)] proporciona una buena predicción de la MCM en mujeres jóvenes.

AGRADECIMIENTOS

Los autores agradecen a la Fundación de Apoyo a la Investigación de Río de Janeiro por su apoyo financiero (beca FAPERJ: E-26 / 111.413 / 2013) y a Fabiana Eramo por la revisión del texto.

Dirección de correo: Dr. Fernando Pompeu, 540 Carlos Chagas Avenue, Zip Code:21941-590, Rio de Janeiro, R.J., Brazil. Phone (+55 21) 3839 6826, Fax (+55 21) 3839 6801, Email: fpompeu@eefd.ufrj.br