Rendimiento Competitivo de Triatletas de Elite que Compiten en Distancia Olímpica: Confiabilidad y Menor Mejora Significativa

Objetivos: La confiabilidad del rendimiento competitivo de los atletas de diferentes deportes provee una estimación del menor cambio significativo en el rendimiento, lo cual es crucial cuando se evalúa a los atletas y cuando se valoran los factores que afectan el rendimiento en un deporte en particular. Por lo tanto, hemos analizado la confiabilidad del rendimiento de atletas que compiten en la prueba de triatlón de distancia olímpica a nivel internacional. Métodos: Se obtuvieron los resultados oficiales, en distintos sitios Web, de diversas pruebas de triatlón llevadas a cabo antes de que se permitiera el “drafting” (correr pegado a otro competidor) en la etapa de ciclismo. Se analizaron los tiempos de 103 atletas que participaron en dos o más de nueve carreras llevadas a cabo en 19 meses. Nuestra medición de la confiabilidad fue la variación característica del tiempo del atleta entre una carrera y otra, calculada como el coeficiente de variación mediante el análisis de los tiempos con transformación log. Resultados: (a) las variaciones características entre una carrera y otra fueron: natación, 1.6%; ciclismo, 2.3% y carrera a pie, 3.6%. Cuando se combinaron, independiente o dependiente de la duración de cada fase (20, 60 y 35 min), estas variaciones produjeron variaciones estimadas en el tiempo total de 1.6% o 2.6% respectivamente, mientras que la variación observada fue del 1.8%. (b) Los tiempos de transición, que estuvieran disponibles para tres carreras, promediaron 89 s para las transiciones combinadas entre la natación y el ciclismo y entre el ciclismo y la carrera. La variación inter individual en estos tiempos en cada carrera fue de 5.2, 5.6 y 7.8 s, o ~ 0.1% del tiempo medio total de 115 minutos. (c) El análisis de la confiabilidad entre todos los posibles pares de carrera no mostraron un efecto substancial del tiempo entre los pares (14 – 567 días). (d) La confiabilidad entre los pares de carreras llevados a cabo a temperaturas ambientales normales fue mejor que cuando al menos uno de los pares de carreras había sido llevado a cabo en condiciones calurosas (variaciones características del 1.6% y 2.0%, respectivamente). (e) El 10% de los mejores triatletas, quienes en promedio fueron un 3.4% más rápidos que el triatleta promedio, exhibieron variaciones substancialmente menores que los otros triatletas respecto del tiempo total (1.1%) y para cada una de las tres etapas (natación, 1.2%; ciclismo, 1.3%; carrera, 2.5%). En los triatlones en donde se permitió el “drafting” en la etapa de ciclismo, la variación en el tiempo total de los mejores triatletas probablemente estuvo dada solo por la carrera a pie y por lo tanto fue de ~ 0.8%. Conclusiones: (a) Los factores que afectan el rendimiento de triatletas de elite actúan en gran medida independientemente en las tres fases. (b) No es posible obtener mejoras significativas en el rendimiento a través de la reducción del tiempo de transición. (c) El rendimiento de los triatletas de elite es notablemente estable a lo largo de un período de 19 meses. (d) El resultado de un triatlón llevado a cabo en un ambiente caluroso es algo menos predecible que el de uno llevado a cabo en condiciones normales. (e) El menor cambio significativo en el tiempo de carrera para los mejores atletas (mitad de la variación en el tiempo total) es de ~ 0.5%, lo cual en los triatlones actuales debe alcanzarse a través de un cambio de al menos 1.2% en la velocidad de carrera a pie.

INTRODUCCION

Cualquiera con un serio interés en el rendimiento de los atletas de más alto nivel debería apreciar la importancia del menor cambio significativo en el rendimiento: el cambio que hace una diferencia significativa a las oportunidades de un atleta de ganar una competencia. El conocimiento de este cambio es necesario para la valoración de los atletas mediante un test de rendimiento y tomar decisiones acerca de los cambios significativos en un individuo o en estrategias de investigación que puedan afectar el rendimiento (Hopkins, 2004).

Para atletas que compiten individualmente y que para ganar deben registrar el mejor tiempo, la mejor distancia o el mejor puntaje, el análisis de la confiabilidad (reproducibilidad o variabilidad) del rendimiento competitivo provee una estimación del menor cambio significativo (Hopkins et al., 1999). El rendimiento de un atleta individual muestra una variación aleatoria de una competencia a la siguiente. Las mejoras o desmejoras en el rendimiento afectan las oportunidades del atleta de ganar una competencia solo si estas son de una magnitud mayor a la mitad de su variación aleatoria. Hasta ahora, los únicos datos publicados en forma completa acerca de la variabilidad del rendimiento competitivo son los de nadadores juveniles (Stewart and Hopkins, 2000), nadadores de elite (Pyne et al., 2004) y corredores de nivel no elite (Hopkins and Hewson, 2001). Por esta razón se necesitan más estudios acerca de la variabilidad del rendimiento competitivo. En el presente estudio nos hemos dedicado a la cuestión de la magnitud de la variabilidad del rendimiento en triatletas de alto nivel.

METODOS

Para este estudio hemos realizado una búsqueda en la Web de los resultados oficiales de triatlones de distancia olímpica. Hasta ese momento, la práctica del drafting (correr en pelotones durante la etapa de ciclismo) no estaba permitida. Hemos limitado arbitrariamente los datos a las carreras llevadas a cabo en un período de 19 meses, como se muestra en la Tabla 1. Para contribuir al análisis de la confiabilidad, los atletas tenían que competir y finalizar en al menos dos competencias. El número de dichos atletas y sus tiempos de carrera se muestran en la Tabla. Para estos atletas, los tiempos medios (en minutos) por etapa fueron: natación, 19.5; ciclismo, 59.8; carrera a pie, 35.1; y tiempo total, 115.0.

En el presente estudio hemos estimado la variabilidad de los tiempos de atletas individuales de una carrera a la otra utilizando los procedimientos previamente descritos para corredores competitivos (Hopkins and Hewson, 2001). En forma resumida, se aplicó el procedimiento de modelado linear mixto (Proc Mixed) del Sistema de Análisis Estadístico (Version 8.2, SAS Institute, Cary, NC) a los tiempos de carrera, a los que se le aplicó la transformación log, y se derivó el coeficiente de variación intra atleta (desviación estándar expresada como un porcentaje de la media) conjuntamente con su límite de probabilidad (confianza) del 90%. El coeficiente de variación intra atleta representa el porcentaje de variación característico en el rendimiento de un atleta de una competencia a otra luego de controlar estadísticamente las diferencias en los tiempos medios de cada competencia.

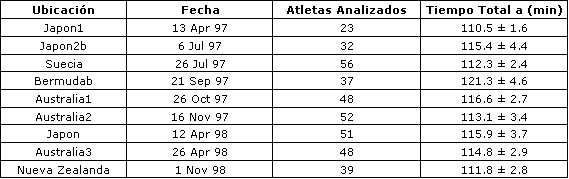
Tabla 1. Triatlones de distancia olímpica y triatletas analizados en el presente estudio. aMedia ± desviación estándar, bRealizado en un ambiente relativamente caluroso (>30ºC)

La variabilidad en cada fase del triatlón contribuye a la variabilidad del tiempo total. Si el rendimiento de un atleta en cada fase es independiente del rendimiento en las otras fases, la variabilidad del tiempo total debería ser igual a la raíz cuadrada de la suma de las varianzas que representan la variabilidad en cada fase. Por otro lado, si el rendimiento de un atleta en cada fase es totalmente dependiente del rendimiento en cada una de las otras fases, la variabilidad del tiempo total debería ser igual a la suma linear de las desviaciones estándar. Nosotros estimamos la variabilidad en el tiempo total combinando las variabilidades en cada fase tanto en forma independiente como dependiente, para realizar la comparación con la variabilidad observada en el tiempo total.

Los análisis descritos previamente fueron llevados a cabo con todos los datos y dividiendo a la muestra total en subgrupos correspondientes al 10%, 20% y 50% de los mejores triatletas, identificados mediante la clasificación de las medias de los cuadrados mínimos del tiempo total de cada atleta a través de todas las carreras. Este procedimiento de clasificación ajusta el tiempo de carrera de cada atleta a la duración media de la carrera y a la duración media de las carreras en las que no participó, por lo que es una forma más precisa de clasificar a los atletas que simplemente promediar los tiempos crudos de carrera (Hopkins and Green, 1995).

Para examinar el efecto del tiempo a través de las carreras sobre la variabilidad intra atleta, hemos computado la variabilidad para cada posible combinación de pares de carreras; y luego hemos graficado los coeficientes de variación resultantes contra el tiempo entre las carreras. También se investigó el efecto de la temperatura ambiental sobre la variabilidad, marcando separadamente los puntos de la gráfica que representan las carreras que fueron apareadas con una de las dos carreras llevadas a cabo en condiciones calurosas (>30ºC, datos provistos conjuntamente con los resultados oficiales). Las líneas de los cuadrados mínimos no ponderados fueron ajustadas a estos puntos y a los puntos que representan los pares de carreras. No se derivaron los límites de confianza para estas líneas y sus comparaciones, debido a la falta de independencia de los puntos.

Las diferencias entre los coeficientes de variación que representan la variabilidad entre carreras fueron consideradas substanciales si su cociente era mayor que 1.10. La razón detrás de esta decisión es la siguiente: el menor cambio significativo en el rendimiento es proporcional a la variabilidad (Hopkins et al., 1999) y, el tamaño de la muestra en estudios llevados a cabo para cuantificar un cambio medio es proporcional al cuadrado de la magnitud del cambio (Hopkins, 2000); por lo tanto un cociente de 1.1 representa un incremento en el tamaño de la muestra de un factor de 1.21 (1.1²), o un incremento del 21%.

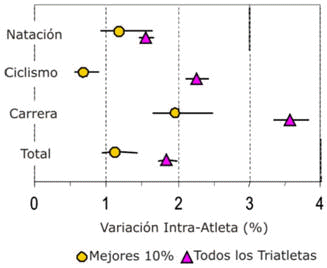
Figura 1. Variación característica en el rendimiento de un triatleta en las etapas de natación, ciclismo y carrera a pie, y en el rendimiento total promediado en nueve triatlones para todos los triatletas y para el 10% de los mejores atletas. Las barras representan el límite de confianza del 90%.

RESULTADOS

La variación característica intra atleta en los tiempos de carrera entre carreras se muestra en la Figura 1. Las variaciones en la figura para todos los atletas son: natación, 1.6%; ciclismo, 2.3%; carrera a pie, 3.6%; total, 1.8%. Cuando se combinaron en forma independiente y dependiente, las variaciones de las tres fases produjeron variaciones estimadas en el tiempo total de 1.6% y 2.6% respectivamente.

El tiempo total de carrera del 10% que representaba a los mejores atletas fue un 3.4% menor que el tiempo medio para todos los atletas. Para estos atletas, las variaciones intra atleta mostradas en la Figura 1 son: natación, 1.2%; ciclismo, 1.3%; carrera a pie, 2.5%; total, 1.1%. Las variaciones estimadas en el tiempo total fueron del 1.0% y del 1.6% para las variabilidades independientes y dependientes en las tres fases. La variabilidad del rendimiento del 20% de los mejores alteas fue apenas diferente de la observada en el 10% de los mejores atletas, pero la variabilidad del 50% de los mejores atletas fue substancialmente mayor.

Los tiempos de transición entre las distintas fases de la carrera solo estuvieron disponibles para tres locaciones (Tabla 2). El tiempo medio de transición fue de 89 segundos para las transiciones entre natación y ciclismo y entre ciclismo y carrera combinadas. La variación intra atleta en el tiempo es equivalente al ~ 0.09% del tiempo medio de carrera de 115 minutos. La variación intra atleta a lo largo de las tres carreras fue un poco menor (4.6 s, o 0.07%)

Tabla 2. Tiempo total de transición en las tres carreras en las que se registraron dichos datos.

Para el análisis de la variación intra atleta entre todos los pares de carreras, el tamaño medio de la muestra fue 19 (rango, 6-32). La gráfica de la variación intra atleta (Figura 2) no mostró un efecto substancial del tiempo entre los pares a través del rango de 14-567 días. La variación característica entre los pares de carreras llevadas a cabo con temperaturas ambientales normales (media, 1.6%) fue menor que la observada cuando al menos una de las carreras del par había sido llevada en condiciones calurosas (media, 2.0%). La variación aleatoria extra adicionada al rendimiento de un atleta en una competencia llevada a cabo en condiciones de calor está dada por √(2(2.02-1.62)) = 1.6%.

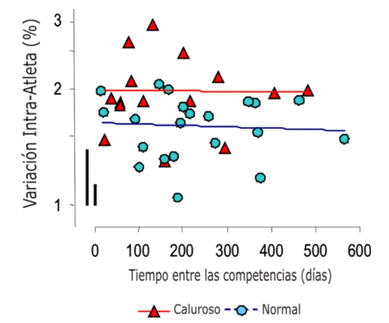
Figura 2. Variación intra atleta (escala log [log scale]) en el rendimiento, entre todos los pares formados con nueve triatlones, graficada versus el tiempo entre las competencias. Los apareamientos y las líneas de regresión se muestran para los pares de competencias de las cuales al menos una se llevó a cabo en condiciones calurosas. Las barras son las desviaciones estándar y representan la variación de muestreo esperada para el menor y el mayor tamaño de la muestra (6 y 32, barras de la izquierda y derecha respectivamente).

DISCUSION

El presente estudio fue llevado a cabo principalmente para determinar el menor cambio significativo en el rendimiento de triatletas de alto nivel. Los análisis también revelaron información útil e interesante acerca de la estabilidad del rendimiento entre las carreras y acerca de las contribuciones de cada una de las fases y de las transiciones al tiempo total de carrera.

Los triatletas que se encontraban dentro del 10% de los mejores atletas tuvieron una variabilidad substancialmente menor en su rendimiento que el triatleta promedio de nivel internacional. En estudios previos también se ha observado una menor variabilidad en los subgrupos de atletas más rápidos (Stewart and Hopkins, 2000; Hopkins and Hewson, 2001; Pyne et al., 2004) lo que presumiblemente refleja una mejor preparación, un ritmo de carrera más consistente, o una mayor motivación entre las carreras. El menor cambio significativo en el rendimiento es de aproximadamente un medio de la variación característica entre carreras (Hopkins et al., 1999), por lo que, para nuestros triatletas de alto nivel este cambio es ~0.5×1.1 = 0.5% del tiempo total de carrera.

Un hallazgo sorprendente fue que los cambios aleatorios en los tiempos para cada una de las fases fueron mayormente independientes unos de los otros. Esto significa que hay algún factor que normalmente afecta al rendimiento del triatleta durante las competiciones que debe actuar predominantemente solo en una fase. Por ejemplo, los cambios en las variables asociadas con la capacidad de resistencia, tales como el consumo máximo de oxígeno, pueden tener o un efecto substancial sobre solo una de las fases o no tienen consecuencias sobre cualquiera de las fases en relación a cualquier otro factor que afecte el rendimiento. Por lo tanto es probable que cualquier estrategia que tenga el propósito de mejorar el tiempo total de carrera de un triatleta en un mínimo del 0.5% debería enfocarse a solo una fase de la carrera.

Antes de que los recientes cambios reglamentarios permitieran la utilización del drafting durante la fase de ciclismo, era posible alcanzar, en principio, una ganancia mínima del 0.5% en cualquier fase; de hecho, todavía puede ser posible alcanzar ganancias significativas en las fase de natación y en la fase de ciclismo siempre y cuando el triatlón sea realizado en un curso con pendientes lo que reduce el efecto del drafting. La ganancia necesaria en la velocidad dependerá de la duración de la fase. La duración de la fase de natación es de aproximadamente un sexto de la duración total, por lo que una mejora del 0.5% en el tiempo total requeriría una mejora del 3% (= 6 × 0.5%) en la velocidad de nado, un objetivo porco realista para un atleta de alto nivel. Las mejoras correspondientes en las velocidades de ciclismo y carrera a pie serían del 1.0% y 1.6% las cuales son más alcanzables. Ahora que se permite el drafting, es claro que los ganadores de medallas deben dejar el agua a tiempo para juntarse con el primer pelotón de bicicletas, ya que estos atletas son generalmente más fuertes en la fase de ciclismo y sacan una ventaja que es difícil de acortar en la fase de carrera a pie. Por lo tanto, los mejores triatletas ahora deben ser lo suficientemente rápidos en la fase de natación como para juntarse con el primer pelotón de bicicletas, y deberían enfocar sus estrategias de entrenamiento en mejorar el rendimiento en la fase de carrera. Si ahora asumimos que la única variación en el tiempo total proviene de la fase de carrera, y que la variación intra atleta en la fase de carrera de los mejores atletas es similar a observada por nosotros (2.5%), la variación en el tiempo total sería 35/115×2.5% = 0.8%; el menor cambios significativo en el tiempo total sería ~0.5×0.8 = 0.4%, y este cambio debería ser alcanzado por un cambio del ~0.5×2.5% = 1.2% en la velocidad de carrera.

No se pueden obtener ganancias substanciales en las transiciones, debido a que la variación en el tiempo de transición representa <0.1% del tiempo total. En los triatlones donde se permite el drafting, la variación en la transición entre la natación y el ciclismo podría ser lo suficientemente grande, en principio, como para afectar la oportunidad de un atleta de alcanzar al primer pelotón de bicicletas. Sin embargo, la mayor parte de la variación en la transición se debe a la variación aleatoria intra atleta, y es difícil imaginar como un atleta podría modificar dicha variación pare mejorar el tiempo de transición.

Otro hallazgo que debe destacarse el la notable estabilidad del rendimiento de los triatletas de nivel internacional. De hecho, como puede observarse en la Figura 2, no hay nada que indique un incremento en la variabilidad, incluso a lo largo de 19 meses, lo cual implica que los atletas mantienen su forma física por al menos este período. Las barras de error en la figura muestran que la dispersión en la variación intra atleta se debe principalmente a la variación del muestreo en las estimaciones más que a verdaderas diferencias en la variación entre las carreras.

Por último, es bastante claro que el rendimiento fue más variable para aquellos triatlones llevados a cabo en condiciones calurosas. La variabilidad adicionada por el calor es los suficientemente grande como para que algunos triatletas se encuentren en desventaja con respecto a otros. Es posible que una estrategia de aclimatación agresiva pueda reducir esta variabilidad hasta un nivel insignificante, pero algunos atletas pueden estar inherentemente en desventaja cuando compiten en el calor sin importar cuan bien aclimatados se encuentren.