Un novedoso método para la predicción de 1MR utilizando el perfil de carga-velocidad

Una máxima repetición (1MR) se define como la carga externa máxima (kg) que una persona puede levantar para una sola repetición [Suchomel 2016]. Además, los tests de 1MR tienen una fiabilidad excelente, se relacionan con movimientos deportivos biomecánicamente similares (por ej., sentadillas y saltos) y pueden servir como una herramienta prescriptiva eficaz (% 1MR) [Thompson 2020]. A pesar de esto, se impone una gran demanda al sistema neuromuscular, lo que a menudo hace que los tests regulares de 1MR no sean factibles, particularmente en deportes multifacéticos (como deportes de equipo o de campo) debido a la importancia del entrenamiento técnico, los horarios competitivos ocupados y los viajes [Shattock 2020]. Por lo tanto, los tests máximos frecuentes podrían crear una fatiga no deseada, lo que podría afectar al rendimiento durante todo el año. Si bien es poco probable que esto sea problemático en entornos donde los tests de 1MR son relativamente estables (por ej., deportes de fuerza), la fuerza máxima podría fluctuar en los atletas que compiten en estos deportes debido a las prioridades del entrenamiento [Shattock 2020], el sueño [Reilly 1994], la nutrición [Cribb 2007] y/o fatiga [Enoka 2008]. Como resultado, estrategias alternativas como la predicción de 1MR a partir de los datos del perfil de carga-velocidad (LVP) podrían ser una estrategia eficaz para manipular la carga (es decir, la autorregulación), que se cree que es vital para optimizar el desarrollo deportivo [Greig 2020].

Normalmente, los perfiles LVP se construyen utilizando una combinación de cargas ligeras y pesadas (30% 1MR a 100% 1MR) en un ejercicio no balístico [Thompson 2020 y 2021]. A pesar de esto, los equivalentes balísticos (sentadilla con salto con carga) a menudo se prescriben con más frecuencia que los ejercicios no balísticos con estas cargas más ligeras (por ej., peso corporal al 60% de 1MR) dados los mayores rendimientos mecánicos, una relación más estrecha con acciones deportivas específicas (por ej., saltar) y períodos más prolongados de aceleración positiva [Cormie 2010, Tricoli 2005]. Por lo tanto, al utilizar ejercicios balísticos y no balísticos dentro de los LVP, podría decirse que podría desarrollarse un modelo más confiable, válido y prácticamente representativo, lo que permitiría una mayor utilidad en la práctica. Además, la combinación de estos datos más válidos con la sofisticación del modelo cuadrático podría ofrecer predicciones mejoradas para un movimiento complejo de peso libre como la sentadilla trasera. Recientemente, Steve W. Thompson de la Sheffield Hallam University (Reino Unido), llevó a cabo un estudio al respecto cuyo objetivo fue investigar si se podía predecir 1MR a partir de los datos de la carga-velocidad. Específicamente, para comparar si la selección del ejercicio (método 'combinado' de sentadilla traseras vs sentadilla con salto y sentadilla trasera) y la construcción del modelo (lineal vs cuadrática) afecta la validez predictiva del LVP usando un método novedoso de extrapolación (80% 1MR) para estimar la fuerza máxima.

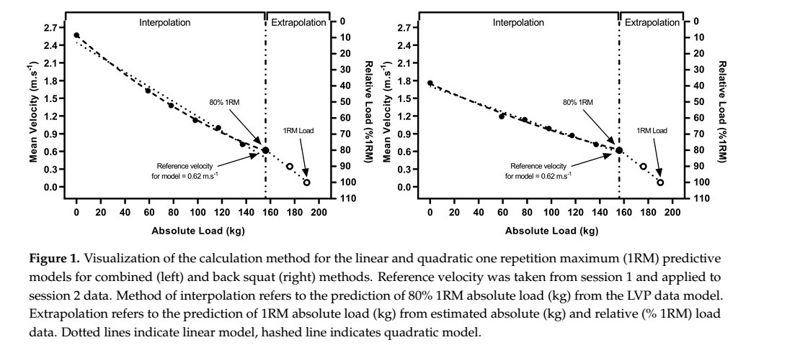
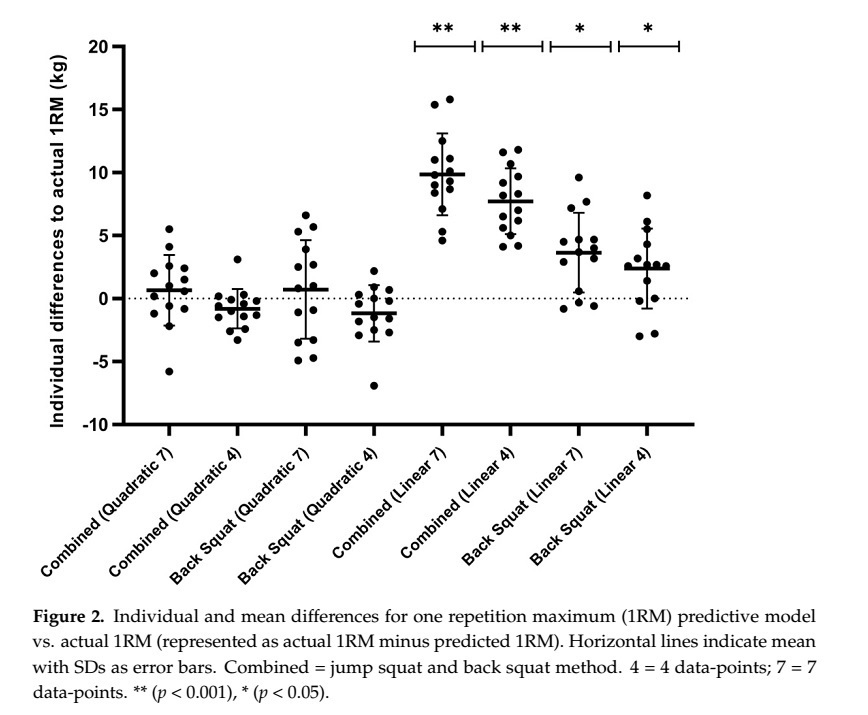
Catorce hombres entrenados en fuerza se sometieron a 1MR inicial en sentadilla trasera con peso libre, seguidas de dos cargas LVP, durante tres sesiones. Los perfiles se construyeron mediante un método combinado (sentadilla con salto (carga 0, 30–60% 1MR) + sentadilla trasera (70–100% 1MR)) o sólo sentadilla trasera (carga 0, 30–100% 1MR) en incrementos de 10%. Se aplicó un modelo de regresión cuadrática y lineal a los datos para estimar el 80% de 1MR (kg) utilizando la velocidad media del 80% de 1MR identificada en la carga LVP como punto de referencia, con carga (kg), luego extrapolada para predecir 1MR. La predicción de 1MR se basó en datos de la LVP dos y se dedujo mediante análisis de varianza, tamaño del efecto (g/ɳ²_p), coeficientes de correlación de Pearson (r), t-tests apareados, error estándar de estimación (SEE) y límites de concordancia (LOA) p <0.05.

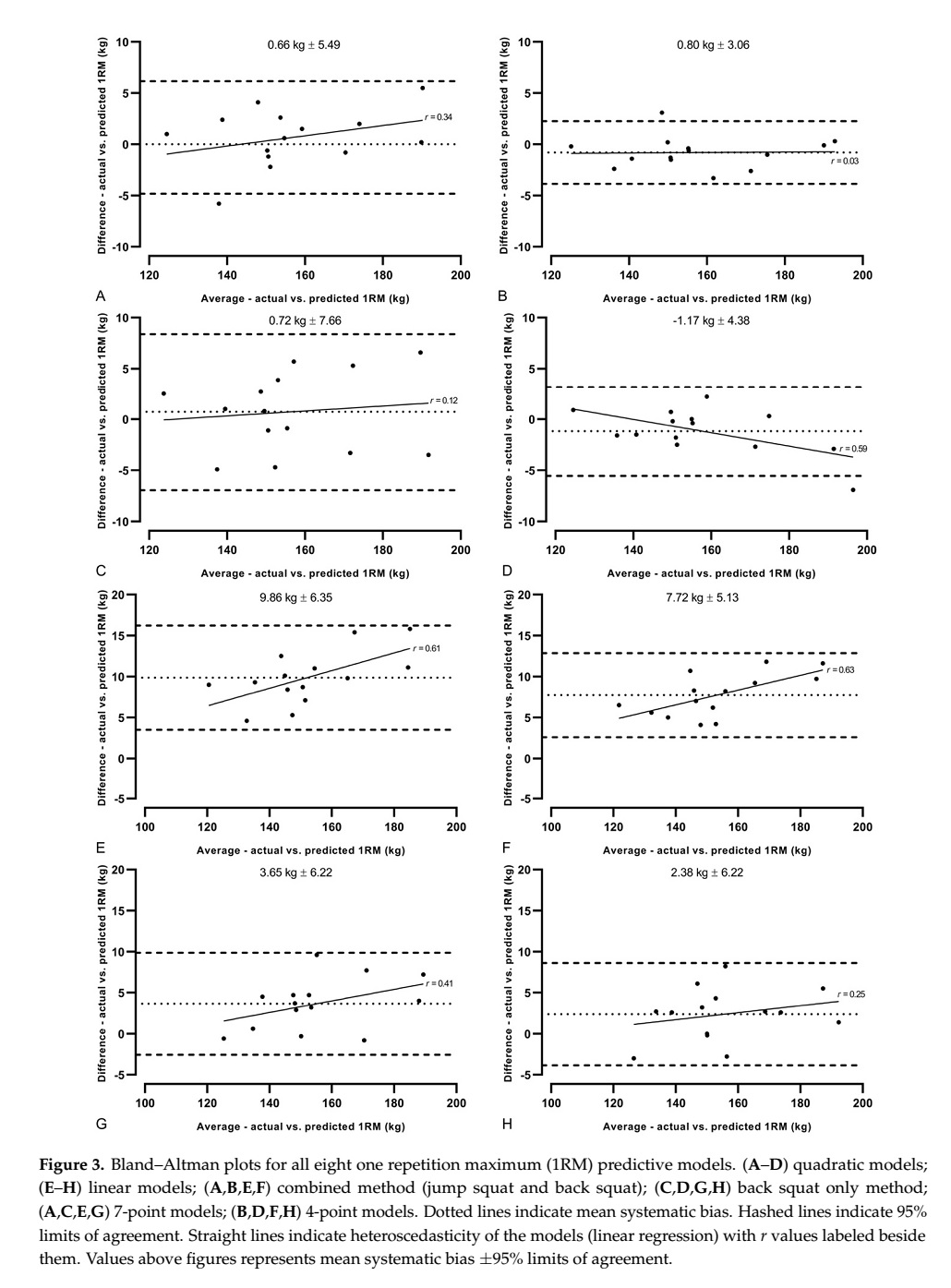
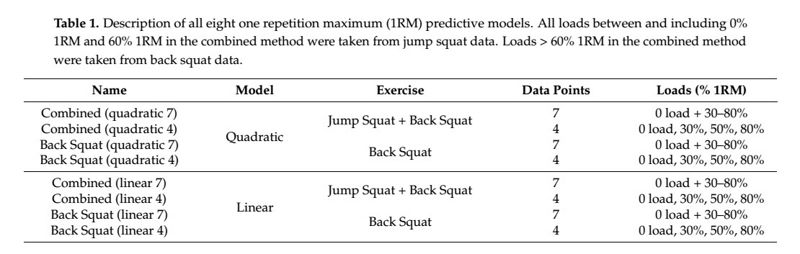
Todos los modelos informaron un sesgo sistemático <10 kg, r >0.97 y SEE <5 kg; sin embargo, todos los modelos lineales fueron significativamente diferentes del 1MR medido (p = 0.015 <0.001). Se observaron diferencias significativas entre los modelos cuadráticos y lineales para los métodos combinados (p <0.001; ɳ²_p = 0.90) y sentadilla (p = 0.004, ɳ²_p = 0.35). Se observaron diferencias significativas entre los ejercicios al aplicar el modelado lineal (p <0.001, ɳ²_p = 0.67-0.80), pero no cuadrático (p = 0.632-0.929, ɳ²_p = 0.001-0.18).

El modelado cuadrático que emplea el método combinado proporcionó la mayor validez predictiva. Por lo tanto, los profesionales deben utilizar este método cuando busquen predecir 1MR diario como un medio de autorregulación de la carga.