Un Novedoso Método para la Predicción de 1MR Utilizando el Perfil de Carga-Velocidad: Una Comparación de Modelos

El objetivo del estudio fue comparar diferentes modelos predictivos en una estimación de 1 máxima repetición (1MR) a partir de datos del perfil de carga-velocidad (LVP). Catorce hombres entrenados en fuerza se sometieron a 1MR inicial en sentadilla trasera con peso libre, seguidas de dos cargas LVP, durante tres sesiones. Los perfiles se construyeron mediante un método combinado (sentadilla con salto (carga 0, 30–60% 1MR) + sentadilla trasera (70–100% 1MR)) o sólo sentadilla trasera (carga 0, 30–100% 1MR) en incrementos de 10%. Se aplicó un modelo de regresión cuadrática y lineal a los datos para estimar el 80% de 1MR (kg) utilizando la velocidad media del 80% de 1MR identificada en la carga LVP como punto de referencia, con carga (kg), luego extrapolada para predecir 1MR. La predicción de 1MR se basó en datos de la LVP dos y se dedujo mediante análisis de varianza, tamaño del efecto (g/ɳ2p), coeficientes de correlación de Pearson (r), t-tests apareados, error estándar de estimación (SEE) y límites de concordancia (LOA) p <0.05. Todos los modelos informaron un sesgo sistemático <10 kg, r >0.97 y SEE <5 kg; sin embargo, todos los modelos lineales fueron significativamente diferentes del 1MR medido (p = 0.015 <0.001). Se observaron diferencias significativas entre los modelos cuadráticos y lineales para los métodos combinados (p <0.001; ɳ2p = 0.90) y sentadilla (p = 0.004, ɳ2p = 0.35). Se observaron diferencias significativas entre los ejercicios al aplicar el modelado lineal (p <0.001, ɳ2p = 0.67-0.80), pero no cuadrático (p = 0.632-0.929, ɳ2p = 0.001-0.18). El modelado cuadrático que emplea el método combinado proporcionó la mayor validez predictiva. Por lo tanto, los profesionales deben utilizar este método cuando busquen predecir 1MR diario como un medio de autorregulación de la carga.

The study aim was to compare different predictive models in one repetition maximum (1RM) estimation from load-velocity profile (LVP) data. Fourteen strength-trained men underwent initial 1RMs in the free-weight back squat, followed by two LVPs, over three sessions. Profiles were constructed via a combined method (jump squat (0 load, 30–60% 1RM) + back squat (70–100% 1RM)) or back squat only (0 load, 30–100% 1RM) in 10% increments. Quadratic and linear regression modeling was applied to the data to estimate 80% 1RM (kg) using 80% 1RM mean velocity identified in LVP one as the reference point, with load (kg), then extrapolated to predict 1RM. The 1RM prediction was based on LVP two data and analyzed via analysis of variance, effect size (g/η2p), Pearson correlation coefficients (r), paired t-tests, standard error of the estimate (SEE), and limits of agreement (LOA). p < 0.05. All models reported systematic bias < 10 kg, r > 0.97, and SEE < 5 kg, however, all linear models were significantly different from measured 1RM (p = 0.015 <0.001). Significant differences were observed between quadratic and linear models for combined (p < 0.001; η2p = 0.90) and back squat (p = 0.004, η2p = 0.35) methods. Significant differences were observed between exercises when applying linear modeling (p < 0.001, η2p = 0.67–0.80), but not quadratic (p = 0.632–0.929, η2p = 0.001–0.18). Quadratic modeling employing the combined method rendered the greatest predictive validity. Practitioners should therefore utilize this method when looking to predict daily 1RMs as a means of load autoregulation.

INTRODUCCIÓN

Una máxima repetición (1MR) se define como la carga externa máxima (kg) que una persona puede levantar para una sola repetición [1]. Además, los tests de 1MR tienen una fiabilidad excelente, se relacionan con movimientos deportivos biomecánicamente similares (por ej., sentadillas y saltos) y pueden servir como una herramienta prescriptiva eficaz (% 1MR) [1-4]. A pesar de esto, se impone una gran demanda al sistema neuromuscular, lo que a menudo hace que los tests regulares de 1MR no sean factibles, particularmente en deportes multifacéticos (como deportes de equipo o de campo) debido a la importancia del entrenamiento técnico, los horarios competitivos ocupados y los viajes [5]. Por lo tanto, los tests máximos frecuentes podrían crear una fatiga no deseada, lo que podría afectar al rendimiento durante todo el año [5]. Si bien es poco probable que esto sea problemático en entornos donde los tests de 1MR son relativamente estables (por ej., deportes de fuerza), la fuerza máxima podría fluctuar en los atletas que compiten en estos deportes debido a las prioridades del entrenamiento [5], el sueño [6], la nutrición [7] y/o fatiga [8]. Como resultado, estrategias alternativas como la predicción de 1MR a partir de los datos del perfil de carga-velocidad (LVP) podrían ser una estrategia eficaz para manipular la carga (es decir, la autorregulación), que se cree que es vital para optimizar el desarrollo deportivo [9].

Normalmente, los LVP se construyen utilizando una combinación de cargas ligeras y pesadas (30% 1MR a 100% 1MR) en un ejercicio no balístico [11,29]. A pesar de esto, los equivalentes balísticos (sentadilla con salto con carga) a menudo se prescriben con más frecuencia que los ejercicios no balísticos con estas cargas más ligeras (por ej., peso corporal al 60% de 1MR) dados los mayores rendimientos mecánicos, una relación más estrecha con acciones deportivas específicas (por ej., saltar) y períodos más prolongados de aceleración positiva [30-34]. Por lo tanto, al utilizar ejercicios balísticos y no balísticos dentro de los LVP, podría decirse que podría desarrollarse un modelo más confiable, válido y prácticamente representativo, lo que permitiría una mayor utilidad en la práctica. Además, la combinación de estos datos más válidos con la sofisticación del modelo cuadrático podría ofrecer predicciones mejoradas para un movimiento complejo de peso libre como la sentadilla trasera. Por lo tanto, el objetivo de este estudio fue investigar si se podía predecir 1MR a partir de los datos de la carga-velocidad. Específicamente, para comparar si la selección del ejercicio (método 'combinado' de sentadilla traseras vs sentadilla con salto y sentadilla trasera) y la construcción del modelo (lineal vs cuadrática) afecta la validez predictiva del LVP usando un método novedoso de extrapolación (80% 1MR) para estimar la fuerza máxima.

MATERIALES Y MÉTODOS

Sujetos

Catorce hombres sanos, entrenados en fuerza (fuerza relativa >1.5 masa corporal) (edad: 26.0 3.8 años; masa corporal: 82.5±9.4 kg; estatura: 174.7±4.6 cm; fuerza relativa: 1.95±0.2 kg·pc-1) se ofrecieron como voluntarios para este estudio. La aprobación ética se otorgó a través del consejo de ética de la institución (ER13605026) de acuerdo con la séptima revisión (2013) de la declaración de Helsinki. Además de la fuerza relativa, se pidieron 12 meses de experiencia en entrenamiento de la fuerza y competencia técnica en los ejercicios de sentadilla trasera con peso libre y sentadilla cargada con salto. Se proporcionó consentimiento informado verbal y escrito antes de las pruebas.

Procedimientos

Los sujetos acudieron al laboratorio en tres ocasiones, cada una separada por un mínimo de 72 hs. No se permitió ningún ejercicio adicional para la parte inferior del cuerpo 48 hs antes y durante la recopilación de los datos. Todas las repeticiones se realizaron utilizando una barra de pesas calibrada de 20 kg y discos de competición aprobados por la Federación Internacional de Halterofilia (Werksan, Akyurt, Pavo). Se adoptó una técnica de sentadilla con barra alta hacia atrás que involucraba la barra apoyada en la parte superior de los músculos trapecios y usando un agarre neutral. Los sujetos seleccionaron por sí mismos el ancho de la cadera y la posición del pie, que se registró y estandarizó en todas las sesiones. Un levantamiento se consideró exitoso cuando la cadera estaba debajo de la rodilla con un desplazamiento mínimo y las extremidades inferiores estaban completamente extendidas al ascender. La sentadilla con salto se estandarizó de manera idéntica a la sentadilla trasera, pero se requirió que los sujetos abandonaran completamente el piso después del ascenso. La técnica y la profundidad fueron evaluadas por un entrenador experimentado y acreditado de Fuerza y ​​Acondicionamiento (S&C, Strength and Conditioning) y un análisis de video 2D retrospectivo (iPhone 7, iOS 14.4.4, Apple, Cupertino, CA, EE. UU.), para garantizar que la profundidad de cada repetición fuera constante. La función de caída del transductor de posición lineal Gymaware (versión 2.9.4, Kinetic, Canberra, Australia) también se utilizó para comprobar el desplazamiento de la barra.

Prueba de 1MR (visita 1)

La masa corporal (kg) (Kistler, 9286A, Winterthur, Suiza), la estatura (cm) (Seca, Leicester, Hamburgo, Alemania) y la estimación real de 1MR se recopilaron durante la visita inicial. Luego se realizó un calentamiento individualizado y estandarizado utilizando una combinación de estiramiento estático, movilidad dinámica, ejercicios de activación, trabajo ligero con barra y saltos con el peso corporal. También se produjo una familiarización de realizar las fases concéntricas con "máxima intención y velocidad".

Luego, los sujetos fueron sometidos a un protocolo de 1MR incremental en la sentadilla trasera con peso libre que consistía en realizar repeticiones en una serie de cargas incrementales: 50% (cinco repeticiones); 70% (tres repeticiones); 80% (dos repeticiones); 85%, 90% y 95% (una repetición) del valor de 1MR estimado, seguido de hasta cinco intentos para encontrar un 1MR verdadero. El 1MR se determinó cuando el sujeto y el investigador principal acordaban que no se podía levantar más peso o se producía un intento fallido. Además, se prescribió un descanso de 3-5 minutos entre cada carga.

Perfil de carga-velocidad (visitas 2 y 3)

Las visitas dos y tres fueron idénticas desde el punto de vista del procedimiento. Los sujetos realizaron un LVP incremental en los ejercicios de sentadilla trasera y sentadilla con salto. Todas las cargas se determinaron como un porcentaje de 1MR de sentadilla trasera de la primera visita. Se utilizaron un Gymaware (muestreo cada 2 mm de desplazamiento) y un iPad mini de cuarta generación (iOS 14.0.1, Apple, Cupertino, CA, EE. UU.) para medir la velocidad media de cada repetición [29]. El Gymaware estaba ubicado en el extremo derecho, a 10 mm del extremo y perpendicular a la barra.

Antes de la recopilación de los datos, los sujetos completaron el mismo calentamiento estandarizado de la primera visita además de las repeticiones con peso corporal (usando una barra de madera) en la sentadilla trasera y la sentadilla con salto. Luego se realizaron las siguientes cargas secuencialmente en ambos ejercicios: carga 0 (cinco repeticiones), seguida de 30%, 40% (tres repeticiones), 50% y 60% de 1MR (dos repeticiones). Luego, los participantes continuaron con la sentadilla trasera sólo para cargas del 70% (dos repeticiones), 80%, 90% y 100% de 1MR (una repetición). Los participantes recibieron hasta tres intentos para elevar el valor de 1MR logrado en la visita uno. Se administraron cinco minutos de descanso entre las cargas, con tres minutos entre ejercicios en cada carga. Se instruyó a los sujetos para que realizaran la fase concéntrica de cada repetición con "máxima intención y velocidad". La velocidad media se definió como la velocidad media registrada en toda la fase concéntrica de ambos ejercicios. El punto de inicio y de finalización de la fase concéntrica se definió según el sistema de procesamiento y filtrado de datos del fabricante.

Predicción 1MR

Los modelos y métodos empleados en el presente estudio tienen cinco factores novedosos: (1) la utilización del 80% de la velocidad media de 1MR como la constante (punto de referencia) dentro de las ecuaciones predictivas; (2) una comparación entre modelos predictivos lineales y cuadráticos; (3) una combinación de ejercicios de peso libre balísticos (sentadilla con salto) y no balísticos (sentadilla trasera) en comparación con ejercicios no balísticos (sentadilla trasera) solamente; (4) una combinación de interpolación y extrapolación para estimar la carga máxima; y (5) validación del modelo mediante el uso de una serie de datos para ajustar el modelo y luego una nueva serie de datos del LVP para predecir 1MR.

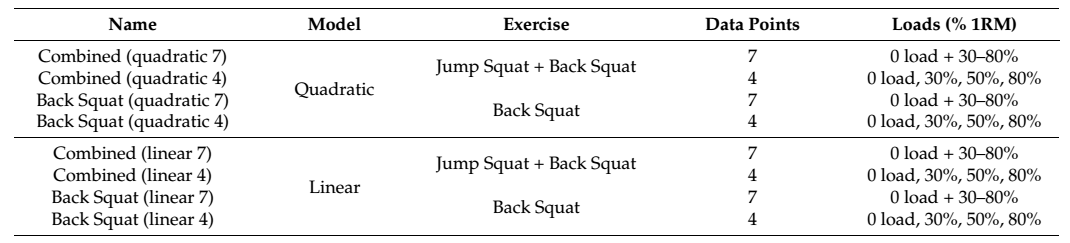
Se crearon ocho LVP para cada individuo después de la recopilación de datos (Tabla 1). Los datos de la velocidad media del método combinado se utilizaron para cuatro de los perfiles, y los datos de velocidad media de la sentadilla sólo se aplicaron a los otros cuatro. Además, se produjo un perfil de cuatro puntos (por ej., Combinado (4 cuadrático)) y de siete puntos (por ej., sentadilla trasera (7 lineal))
para cada una de las condiciones (Tabla 1). Los datos de velocidad para cargas entre 0 carga y 60% 1MR se tomaron de la sentadilla con salto, y cualquier cosa más pesada se tomó de la sentadilla trasera al construir los modelos combinados. Todos los datos de la velocidad (carga 0 a 100% 1MR) se tomaron a partir de la sentadilla trasera al construir los modelos de sentadilla trasera. Luego se aplicó una función cuadrática o lineal a los datos. Los modelos se ajustaron utilizando la carga absoluta (kg) como variable independiente y la velocidad media (m·seg-1) como variable dependiente. La función LINEST se utilizó en Microsoft Excel (Microsoft Excel, Microsoft, Albuquerque, NM, EE. UU.) para determinar los parámetros del modelo para las funciones cuadráticas y lineales. Luego, ambas ecuaciones se reorganizaron para resolver x:
modelo cuadrático:

modelo lineal:

Tabla 1. Descripción de los ocho modelos predictivos de una repetición máxima (1MR). Todas las cargas comprendidas entre 0% 1MR y 60% 1MR en el método combinado se tomaron a partir de los datos de la sentadilla con salto. Las cargas >60% 1MR en el método combinado se tomaron de los datos de la sentadilla trasera.

La velocidad media al 80% 1MR se tomó de la sesión uno y se aplicó a los datos de perfil de la sesión dos, actuando como la velocidad de referencia para cada modelo, es decir, estimando los kg que correspondían al 80% de la velocidad media de 1MR, mediante un método de interpolación. Además, se seleccionó el 80% de 1MR como la velocidad de referencia, ya que la literatura previa ha encontrado que esta es la carga más pesada que demuestra una fiabilidad aceptable de la velocidad media [11]. A continuación, se predijo 1MR mediante un método de extrapolación del 80% al 100% de 1MR utilizando únicamente la carga absoluta (kg) y la relativa (% 1MR). Esto se logró simplemente aumentando la carga absoluta predicha (80% equivalente a 1MR) en un 20% para igualar la carga predicha de 1MR. Se pueden ver ejemplos de los modelos predictivos en la Figura 1.

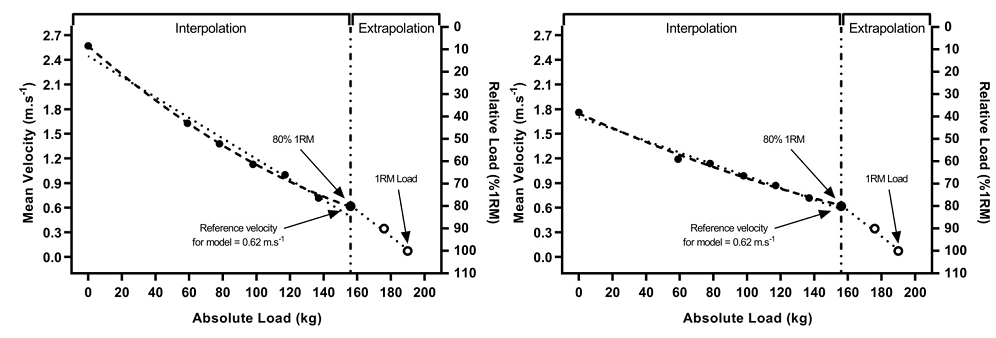
Figura 1. Visualización del método de cálculo para los modelos predictivos lineal y cuadrático de una repetición máxima (1MR) para los métodos combinados (izquierda) y sentadilla trasera (derecha). La velocidad de referencia se tomó de la sesión 1 y se aplicó a los datos de la sesión 2. El método de interpolación se refiere a la predicción del 80% de la carga absoluta de 1MR (kg) a partir del modelo de datos del LVP. La extrapolación se refiere a la predicción de la carga absoluta de 1MR (kg) a partir de los datos estimados de la carga absoluta (kg) y de la relativa (% 1MR). Las líneas punteadas indican un modelo lineal, la línea discontinua indica un modelo cuadrático.

Análisis estadístico

Todos los datos se evaluaron para determinar la distribución normal y los supuestos del modelo relevantes para las variantes lineales y cuadráticas. La validez predictiva de cada modelo se evaluó comparando los valores estimados con los 1MR medidos utilizando t-tests de muestras apareadas, tamaños del efecto (ES) de Hedges g, límites de acuerdo (LOA), correlación r de Pearson y error estándar de la estimación (SEE). Las magnitudes del ES se interpretaron como: trivial (<0.2); pequeño (0.2-0.59); moderado (0.6-1.19); grande (1.19-2.0); muy grande (>2.0) [35]. Las magnitudes r de Pearson se interpretaron como: trivial (<0.1); pequeño (0.1-0.29); moderado (0.3-0.49); alto (0.5-0.69); muy alto (0.7-0.89); y prácticamente perfecto (> 0,9) [11]. Se usó un análisis de varianza de medidas repetidas de dos vías (ANOVA) (ejercicio × modelo) con correcciones post-hoc de Bonferroni para evaluar las diferencias entre modelos y los efectos de interacción relevantes usando diferencias absolutas (1MR directo - 1MR predicho) además del 95% de intervalos de confianza (IC) y ES cuadrático parcial (η2p). Cuando se violó la esfericidad (evaluada mediante las pruebas de esfericidad de Mauchly), se aplicó la corrección de efecto Greenhouse-Geisser. El nivel alfa se fijó en p <0.05. Para los análisis estadísticos se utilizó SPSS (24.0, IBM, Nueva York, NY, EE. UU.) y Microsoft Excel.

Resultados

Todos los datos se distribuyeron normalmente y cumplieron con los supuestos necesarios antes del análisis, o se aplicaron las correcciones apropiadas. El test de 1MR medido fue 157.0±19.4 kg. Las medias, las SDs y los IC del 95% de los datos de 1MR predichos se pueden encontrar en la Tabla 2. Se observaron correlaciones prácticamente perfectas (r >0.97) para todos los modelos predictivos en comparación con los datos de 1MR medidos (Tabla 1). El modelo de sentadilla trasera (cuadrático 7) arrojó el SEE más grande (4.06 kg), con los modelos restantes < 4kg (Tabla 2). Los cuatro modelos predictivos cuadráticos informaron un ES trivial (g = −0.06-0.04), en comparación con los modelos lineales para la sentadilla trasera y los métodos combinados, que informaron un ES moderado (g = 0.52) y pequeño (g = 0.12-0.40), respectivamente (Tabla 2).
Las diferencias medias en el modelo predicho y medido de 1MR se pueden ver en la Figura 2. Los cuatro modelos cuadráticos produjeron diferencias que van desde -1.2 a 0.7 kg, menor que la de los modelos lineales, que van desde 2.4 a 9.9 kg (Figura 2, Tabla 1). Se informaron pequeños sesgos sistemáticos para los cuatro modelos cuadráticos (-1.17-0.73 kg), con un error aleatorio de ±3.09-7.67 kg, mientras que todos los modelos lineales subestimaron la 1MR predicha (2.37-9.87 kg), con un error aleatorio de 5.11 a 6.34 kg siendo observado (Figura 3).

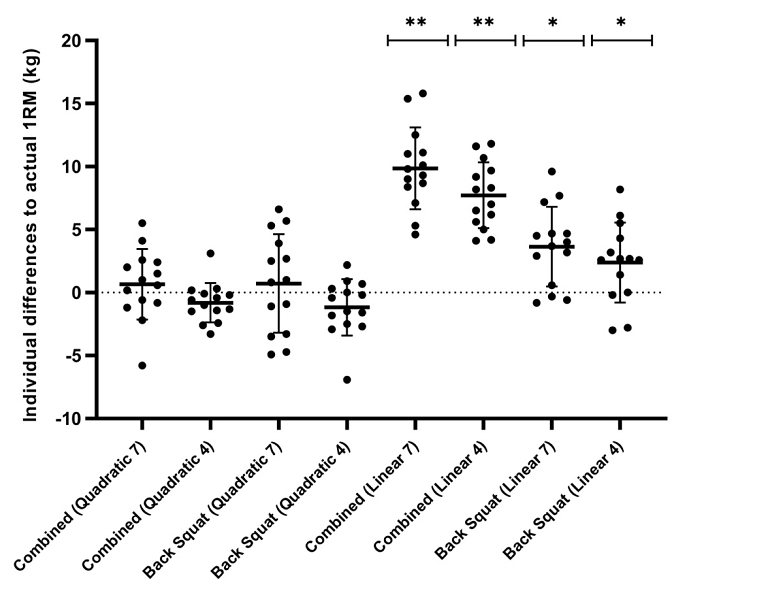
Figura 2. Diferencias individuales y medias para un modelo predictivo máximo de repetición (1MR) vs 1MR real (representado como 1MR real menos 1MR predicha). Las líneas horizontales indican la media con las SDs como barras de error. Combinado = método de sentadilla con salto y sentadilla trasera. 4 = 4 puntos de datos; 7 = 7 puntos de datos. ** (p <0.001), * (p <0.05).

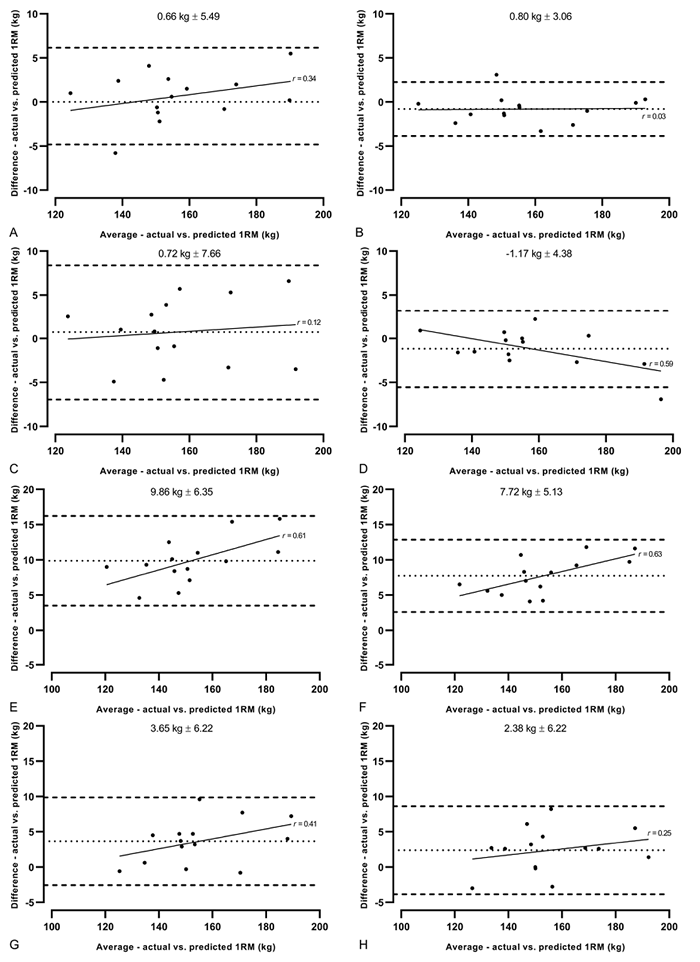
Figura 3. Gráficos de Bland-Altman para los ocho modelos predictivos de una repetición máxima (1MR). (A–D) modelos cuadráticos; (E–H) modelos lineales; (A, B, E, F) método combinado (sentadilla con salto y sentadilla trasera); (C, D, G, H) método exclusivo de sentadilla trasera; (A, C, E, G) modelos de 7 puntos; (B, D, F, H) Modelos de 4 puntos. Las líneas punteadas indican el sesgo sistemático promedio; las líneas discontinuas indican límites de concordancia del 95%. Las líneas rectas indican heterocedasticidad de los modelos (regresión lineal) con valores de r etiquetados al lado. Los valores por encima de las cifras representan el sesgo sistemático promedio ±95% de los límites de acuerdo.

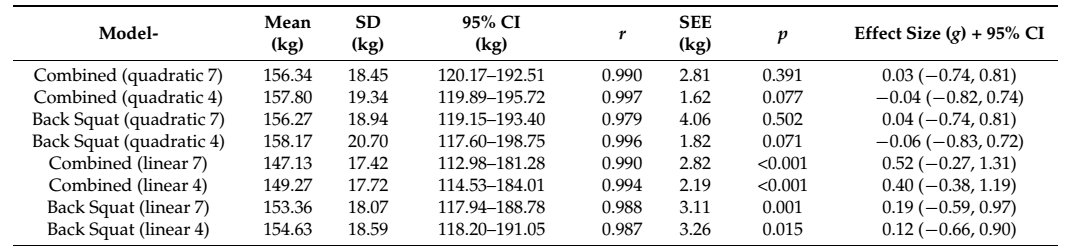
Tabla 2. Datos descriptivos de una máxima repetición (1MR) (medias y SD) con intervalos de confianza (IC) del 95%, coeficiente de correlación de Pearson (r), error estándar de la estimación (SEE), valores p y tamaños del efecto g de Hedges (+95% IC) para los ocho modelos predictivos. 1MR medido = 157.0±19.4 kg. 4 = 4 puntos de datos y 7 = 7 puntos de datos utilizados para construir el modelo. p <0.05.

Se observó una interacción bidireccional significativa entre el ejercicio y el modelo (F(1.65, 21.48) = 23.95, p <0.001, η2p = 0.65), con efectos principales simples observados en todos los modelos (combinados: F(2.01, 26.15) = 121.47, p <0.001, η2p = 0.90; sentadilla trasera: F(1.93, 25.10) = 7.11, p = 0.004, η2p = 0.35). Al aplicar sólo datos de sentadilla, las pruebas de Bonferroni revelaron diferencias significativas entre los modelos cuadráticos y lineales (4 puntos: 3.55 kg (IC del 95%: 0.22-6.88 kg), p = 0.034; 7 puntos: 2.93 kg (IC del 95%: 0.01-5.85 kg), p = 0.049), pero sin diferencias significativas entre los modelos de 4 y 7 puntos (cuadrático: 1.89 kg (IC del 95%: −1.55-5.34 kg), p = 0.670; lineal: 1.27 kg (IC del 95%: -1.20-3.75 kg), p = 0.805). Las pruebas post-hoc también revelaron diferencias significativas entre los modelos cuadráticos y lineales (4 puntos: 8.52 kg (IC del 95%: 6.41 a 10.64 kg), p <0.001; 7 puntos: 9.20 kg (IC del 95%: 7.23 a 11.17 kg), p <0.001) y entre los modelos lineales de 4 y 7 puntos (2.14 kg (IC 95%: 0.95-3.33 kg), p = 0.001), pero no cuadrático (1.46 kg (IC 95%: -0.52-3.45 kg), p = 0.235) cuando se utiliza el método combinado.

Se observaron efectos principales simples para el ejercicio al aplicar el modelado lineal (7 puntos: F(1,13) = 51.56, p <0.001, η2p = 0.80; 4 puntos: F(1,13) = 26.60, p <0.001, η2p = 0.67), pero no el modelo cuadrático (7 puntos: F(1,13) = 0.008, p = 0.929, η2p = 0.001; 4 puntos: F(1,13) = 0.24, p = 0.632, η2p = 0.18). Las diferencias medias entre los ejercicios para los modelos lineales fueron 5.34 kg (IC del 95%: 3.11 a 7.58 kg) y 6.21 kg (IC del 95%: 4.34 a 8.08 kg) para los modelos de 4 y 7 puntos, respectivamente, con modelos cuadráticos como 0.37 kg (IC del 95%: -1.27-2.01 kg) y 0,57 kg (IC del 95%: -1.29-1.41 kg) para modelos de 4 y 7 puntos, respectivamente.

Discusión

El objetivo de este estudio fue investigar si se podía predecir 1MR a partir de datos de carga-velocidad. Específicamente, para comparar si la selección del ejercicio (sentadilla trasera vs sentadilla con salto y sentadilla trasera, método "combinado") y la construcción del modelo (lineal vs cuadrático) afectan la validez predictiva del perfil LVP cuando se usa el 80% de 1MR como la velocidad de referencia del modelo.

Los principales hallazgos de esta investigación fueron que 1MR podía predecirse con precisión a partir de datos de la carga-velocidad y que el modelado cuadrático demostró una mayor precisión que el modelado lineal. Además, al aplicar el modelado cuadrático a los datos del LVP, el método combinado fue tan preciso como la condición de la sentadilla trasera, mientras que las diferencias significativas fueron evidentes entre los enfoques con modelado lineal.

Los resultados de este estudio (Tabla 2) apoyan la investigación reciente que destaca la precisión del uso de datos de LVP para la estimación de carga máxima [17,18,24,25,28,36]. A pesar de esto, nuestros datos mostraron discrepancias entre los valores de 1MR estimados modelados linealmente y los 1MR medidos. Se observaron diferencias significativas para los cuatro modelos lineales, con diferencias medias que oscilan entre 2.4 y 9.9 kg (Figura 2). Cuando se aplica a ejercicios con peso libre para la parte inferior del cuerpo, la literatura previa que investiga la validez predictiva de los datos de LVP respalda nuestros hallazgos. Ruf y cols. [16], Lake y cols. [15] y Banyard y cols. [10] todos informaron estimaciones inexactas de 1MR pronosticado que oscilan entre 5 y 40 kg (p <0.05; ES = -1.24-1.04) en el peso muerto y la sentadilla. Curiosamente, en el presente estudio se observaron SEEs mucho más pequeños (2.2-3.3 kg vs 10.6-17.2 kg) y sesgos sistemáticos (2.4-9.9 kg vs 20.0-30.9 kg) en comparación con los datos anteriores [10]. Estas discrepancias pueden explicarse parcialmente por las diferencias en los métodos de extrapolación aplicados. Investigaciones anteriores utilizaron la V1MR como punto de referencia para el modelado predictivo, a pesar de que las investigaciones indican su escasa validez y fiabilidad [11,16,22]. Como resultado, nuestros modelos se basaron en la carga más pesada (80% 1MR) que demostró niveles aceptables de fiabilidad (80% 1MR CV = 5.4–5.7% vs V1MR = 11.8–19.4%) [11,22]. Dada la superior confiabilidad intraindividual de la velocidad media asociada con cargas submáximas [11], es probable que la magnitud del error aleatorio en nuestro modelo se haya reducido.

Nuestro modelado predictivo implicó un proceso de interpolación de una velocidad media más confiable (80% 1MR), seguida de una extrapolación del 80% estimado de 1MR a 1MR (en kgs), mientras que la literatura previa ha estimado típicamente 1MR mediante extrapolación hasta la V1MR [10,16,17,25,36]. El método de la V1RM se basa en el punto de extrapolación que se alinea completamente con la tendencia de los datos, con el modelo requerido para capturar los valores subyacentes que estima.

A menudo, cuando ese punto de interés es la V1MR, la estimación puede verse comprometida porque la tasa de cambio en la velocidad no es tan constante (pendiente <1) en comparación con cargas submáximas. En cambio, la interpolación puede dar cuenta de esto ya que la estimación de valores cae dentro del rango de datos observados, que es más probable que sea capturado por la función del modelo, lo que conlleva a estimaciones menos erróneas. Finalmente, como carga relativa (% 1MR) y absoluta (kg) son ambos datos de razón, se escalan proporcionalmente, es decir, nuestro método de extrapolación de una predicción de 80% a 100% 1MR parece más robusto para la estimación de la carga máxima que la extrapolación a la V1MR. Las investigaciones futuras deberían buscar emplear este método de estimación en otros ejercicios para investigar más a fondo su validez predictiva.

La literatura anterior que aplica el modelado lineal a los datos del LVP ha informado diferencias más pequeñas y errores asociados que nuestro estudio. Se han informado diferencias medias de <5 kg en los ejercicios de media sentadilla y press de banco a partir de métodos de dos puntos y de múltiples puntos [18,24,36], sin embargo, esta investigación normalmente emplea protocolos basados ​​en máquinas Smith. A pesar de las numerosas críticas con respecto a las máquinas Smith y su transferencia a entornos aplicados, la mayor parte de la literatura en este espacio continúa utilizándolas. La investigación sugiere que los resultados mecánicos como la velocidad de despegue (directamente relacionada con la velocidad máxima), la carga máxima levantada y la actividad muscular electromiográfica difieren cuando se realizan ejercicios de máquina Smith en comparación con el peso libre, lo que sugiere que la generalización de esta investigación a contextos más amplios el uso de ejercicios de peso libre es limitado [37-39]. Por lo tanto, la investigación futura debe buscar dilucidar la validez predictiva de los enfoques más representados en la práctica, como los ejercicios de peso libre para la parte superior e inferior del cuerpo.

Este es el primer estudio que compara diferentes modelos predictivos basados ​​en el LVP en un ejercicio de peso libre para la parte inferior del cuerpo. Se evidenció una interacción bidireccional significativa con efectos principales significativos, con todos los modelos lineales subestimando significativamente el valor de 1MR en comparación con sus contrapartes cuadráticas (p <0.05). También fueron evidentes los LOA más grandes, independientemente del ejercicio empleado (Figura 3), lo que indica la superioridad del modelo cuadrático para estimar el valor de 1MR en la sentadilla trasera con peso libre. Curiosamente, el único estudio anterior que probó hipótesis similares fue en el press de banco con máquina Smith e informó que el modelado lineal de múltiples puntos es superior al modelado polinomial de segundo orden [28]. Una máquina Smith está diseñada para limitar el movimiento en los planos sagital y frontal, aumentando potencialmente la confiabilidad de los datos de velocidad y creando una tendencia más lineal [38]. De manera similar, los movimientos de la parte inferior del cuerpo son de naturaleza más compleja (más articulaciones involucradas, mayor desplazamiento y recorrido y una trayectoria de la barra más variada) que la parte superior del cuerpo (generalmente, una trayectoria de barra lineal más vertical), lo que requiere una mayor interacción entre las fuerzas angulares articulares, momentos y velocidades, potencialmente resultando en una relación menos predecible [40]. Por lo tanto, los profesionales deben utilizar modelos predictivos de 1MR más sofisticados basados ​​en el LVP para tener en cuenta la naturaleza menos predecible de los ejercicios de peso libre para la parte inferior del cuerpo. Además, no se observaron diferencias significativas en la validez predictiva basada en el número de puntos de datos utilizados para construir el perfil en este estudio (2 puntos vs multipuntos) [28] así como en el nuestro (4 puntos vs 7 puntos), lo que sugiere que ambos modelos podrían implementarse de manera efectiva al comienzo de una sesión de entrenamiento para actualizar los valores de 1MR diarios rápidamente con sólo unas pocas cargas levantadas.

Al aplicar el modelo lineal, se observó una diferencia media significativamente mayor y un LOA más grande para el método combinado vs sentadilla trasera (p <0.001). Por el contrario, no se observaron diferencias significativas entre los ejercicios al aplicar el modelo cuadrático, lo que sugiere que este modelo tiene un mayor nivel de sofisticación que puede ajustarse a varios tipos de datos de LVP. Investigaciones anteriores han informado una mayor producción mecánica (velocidad, fuerza, potencia) al realizar ejercicios balísticos con cargas ligeras a moderadas en comparación con sus contrapartes no balísticas, principalmente debido al gran período de trabajo negativo (frenado) al final de la fase concéntrica [31,33]. A pesar de esto, los LVP se obtienen típicamente utilizando sólo un ejercicio no balístico, incluso cuando se comienza con 0-30% de 1MR [11,22,25,41]. La captura de datos de carga-velocidad de esta manera podría ser subóptima y menos válida dada la menor producción mecánica reportada [31,33]. Por lo tanto, utilizar el método combinado con modelado cuadrático parece la forma más lógica, válida y efectiva de construir un LVP y predecir 1MR.

A diferencia de la literatura anterior, el estudio actual evaluó la validez predictiva construyendo primero el modelo a partir de los datos de prueba iniciales (es decir, recopilar datos del LVP y determinar la velocidad del 80% 1MR), y luego evaluó posteriormente su validez utilizando los datos recién recopilados de una segunda sesión. Este enfoque proporciona una mayor confianza en que los modelos predictivos pueden estimar las observaciones futuras con una precisión adecuada. Además, el uso del LVP como herramienta longitudinal se basa en la estabilidad de la velocidad en porcentajes relevantes de 1MR, independientemente de las adaptaciones fisiológicas. Si bien es escasa, la literatura previa sugiere que la velocidad media es estable después de turnos de entrenamiento de fuerza agudos (~ 4-6 semanas) [21,42,43], lo que proporciona confianza en los modelos predictivos. Sin embargo, la investigación futura debe buscar indagar más a fondo la estabilidad del LVP a lo largo de períodos de tiempo más largos (por ejemplo, macrociclo completo), así como predecir 1MR en múltiples sesiones, ya que a menudo, los modelos predictivos pueden concluirse erróneamente como válidos y confiables cuando sólo se aplican al valor de los datos de una sesión.

Conclusiones

La predicción de 1MR basada en datos del LVP podría ser una herramienta autorreguladora eficaz para los profesionales de la fuerza y del acondicionamiento físico en el transcurso de un ciclo de entrenamiento. Los resultados de este estudio brindan a los profesionales la confianza de que un modelo cuadrático que utiliza una velocidad media del 80% de 1MR y que utiliza ejercicios balísticos y no balísticos, es un método eficaz para estimar un valor de 1MR de un individuo en la sentadilla con peso libre, lo que garantiza la manipulación de la carga y la gestión de la fatiga se puede lograr por períodos de sesiones. Dada la naturaleza del protocolo, también sería factible para un entrenador emplear este método al comienzo de una sesión de entrenamiento, para estimar el valor de 1MR diario de un atleta, ajustar las cargas de trabajo relevantes y asegurar la paridad entre las cargas prescritas y el estímulo de entrenamiento previsto en ese día. Esto también permitiría a los entrenadores utilizar la integración de la tecnología al comienzo de una sesión de entrenamiento, liberando su tiempo y atención para entrenar durante el resto del tiempo.

Financiamiento: Esta investigación no recibió financiamiento externo.
Conflicto de intereses: Los autores declaran no tener ningún conflicto de intereses.