Validación Cruzada de Ecuaciones para Estimar el Porcentaje de Grasa Corporal Basadas en el BMI en Atletas Universitarias

El propósito de este estudio fue realizar una validación cruzada de tres ecuaciones de índice de masa corporal (BMI) para predecir el porcentaje de grasa corporal (%BF) en atletas universitarias de sexo femenino. Setenta y cinco atletas de sexo femenino de la Asociación Nacional de Deporte Interuniversitario participaron en el estudio. Se midió la talla y peso de cada participante para determinar el BMI. En el estudio se utilizaron tres ecuaciones de regresión para estimar el %BF en base al BMI que fueron previamente desarrolladas por Deurenberg et al. (DBMI-BF), Gallagher et al. (GBMI-BF), y Jackson et al. (JBMI-BF). Se utilizó absorciometría de rayos x de energía dual (DEXA) para obtener los valores de %BF de referencia. Los resultados no mostraron ninguna diferencia significativa (P> 0,05) en los valores medios del %BF obtenidos mediante 2 de las ecuaciones de porcentajes de grasa corporal basadas en el BMI (DBMI-BF = 27,7 ± 2,9%, JBMI-BF = 28,4 ± 4,7%) y los obtenidos con DEXA (27,7 ± 6,2%), mientras que la medición obtenida por la ecuación GBMI-BF (30,2 ± 4,7%) fue significativamente (P <0,05) superior en comparación con el valor de referencia. El error estándar de estimación varió de 4,53% a 4,82%, el error total estuvo entre 4,67% y 5,41%, y los límites de concordancia tomaron valores aprox. de 12,1% por encima y de 9,4% por debajo de los valores de %BF por DEXA para cada ecuación. Debido a los resultados de esta investigación, las ecuaciones de %BF basadas en BMI podrían ser potencialmente utilizadas en las dm^-2eterminaciones realizadas en el campo para estimar el %BF medio para un grupo completo de atletas de sexo femenino, pero no sería apropiado para estimar el %BF individualmente. Por lo tanto, hay que tener mucho cuidado al usar las ecuaciones de %BF basadas en el BMI, para estimar %BF en esta población.

INTRODUCCION

El índice de masa corporal (BMI), también conocido como índice de Quetelet, es la relación entre el peso y la talla del cuerpo. Se ha transformado en el método principal para establecer los estándares y para determinar la prevalencia de sobrepeso y obesidad (16, 25). La ventaja de usar el BMI es que es fácil de evaluar, dado que la talla y el peso son las únicas variables que se necesitan, y además se cometen errores mínimos de medición asociados a la variación intra o inter observador. El índice de masa corporal es ampliamente utilizado para evaluar el riesgo de desarrollar problemas de salud relacionados con el sobrepeso o con el peso insuficiente (1,16,25). Por ejemplo, ACV, enfermedad de las arterias coronarias, hipertensión y diabetes tipo 2 están entre los problemas asociados con un BMI alto (1,16,25), mientras que los trastornos menstruales, la baja densidad mineral ósea y los desórdenes alimenticios están entre los problemas asociados con un BMI sumamente bajo (17). Debido a las consecuencias negativas de los valores de BMI sumamente bajos o altos, la Organización Mundial de la Salud  (25) y el Instituto Nacional de Salud (16) han establecido -puntos de corte para las categorías de BMI tales como; peso insuficiente (BMI <18,5 kg·m^-2), peso normal (BMI entre 18,5 a 24,9 kg·m^-2), sobrepeso (BMI entre 25 a 29,9 kg·m^-2) y obesidad (BMI> 30 kg·m^-2). 

Una desventaja de BMI es que no distingue entre el tejido graso y la masa corporal magra. Los individuos deportistas normalmente tienen un menor porcentaje de grasa corporal (%BF) y una mayor cantidad de masa muscular que la población general. En cualquier BMI dado, un atleta podría tener un menor %BF en comparación con un sujeto que no es atleta (19). Así, el BMI a menudo clasifica de manera errónea dentro de la categoría sobrepeso a atletas con BF normal % (12,18,19,24). Por esta razón, el BMI no parece ser un sustituto apropiado del %BF al determinar la composición corporal de un atleta. Los especialistas de fuerza y acondicionamiento, los nutricionistas asociados al deporte y los entrenadores, normalmente confían en las técnicas de campo rápidas, baratas, como la medición de pliegues cutáneos o análisis de impedancia bioeléctrica para estimar %BF en los grupos de deportistas (2,7,8,10,13).   

En este sentido, se han desarrollado varias ecuaciones de regresión basadas en el BMI que aportan una estimación razonable de %BF en la población general (6,9,11). Las ecuaciones de %BF basadas en el BMI-pueden ser métodos atractivos para estimar el %BF en una instalación deportiva a campo porque pueden ser aplicadas fácilmente en grupos grandes, ya que la talla y el peso son las variables principales que deben ser medidas. Sin embargo, son escasos los datos sobre la exactitud de las ecuaciones de %BF basadas en el BMI para determinar el %BF específicamente en deportistas de edad universitaria de sexo femenino. Por consiguiente, el propósito de este estudio fue realizar una validación cruzada de tres ecuaciones de %BF basadas en el BMI (6,9,11) para estimar el %BF en atletas universitarias femeninas, utilizando absorciometría de rayos x  de energía dual (DEXA) como medición de referencia. Dado que el BMI solo (es decir, cuando no se utiliza en un modelo de regresión) a menudo produce una clasificación errónea de los atletas con BF % normal dentro de la categoría de sobrepeso (18,19,24), planteamos la hipótesis que las ecuaciones de %BF basadas en el BMI no serían exactas para estimar el %BF en esta cohorte.

MÉTODOS

Sujetos

Setenta y cinco deportistas de sexo femenino de la Asociación Nacional de Atletismo Interuniversitario participaron en el estudio y dieron su consentimiento informado por escrito. Las atletas fueron seleccionadas de los equipos de básquetbol, fútbol, tenis y softball de la Universidad de Auburn de Montgomery, Montgomery, AL. En la Tabla 1 se presenta la estadística descriptiva de las participantes. Cada participante completó una encuesta de antecedentes de salud. Las participantes aparentemente saludables, libres de desórdenes cardiopulmonares, metabólicos y/o ortopédicos, y que no estaban embarazadas fueron incluidas en el proceso de recolección de datos. Los datos fueron recolectados de 7:00 a 11:00 de la mañana durante cualquier día de la semana. Se solicitó a las participantes que no comieran o bebieran durante por lo menos 12 horas antes de las pruebas, y que no realizaran ejercicio ni consumieran alcohol 24 horas antes de la evaluación. Este estudio fue aprobado por el Comité de Revisión Institucional de Asuntos Humanos.

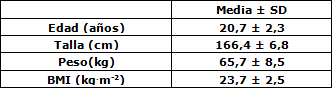
Tabla 1. Estadística descriptive de las participantes del studio (n=75)

Procedimientos 

La talla se midió con un estadiómetro de pared (SECA). Las participantes se colocaron de pie derechas, sin zapatos y con las manos a los costados. Todos los valores de la talla fueron redondeados con una apreciación de 0,1 cm. El peso corporal se midió con un nivel de apreciación de 0,1 kg con una balanza digital calibrada (TANITA BWB-800A). Las mediciones fueron realizadas con las participantes vestidas con ropa liviana y sin zapatos. El índice de masa corporal se calculó dividiendo el peso (kg) por la talla (m2). Todos los valores de BMI se redondearon con una apreciación de 0,1 kg.m^-2. El porcentaje de grasa corporal se estimó usando las siguientes tres ecuaciones de regresión de BMI previamente desarrolladas: Deurenberg et al. (6) (DBMI-BF); Gallagher et al. (9) (GBMI-BF); y Jackson et al. (11) (JBMI-BF). Por favor refiérase a la Tabla 2 para ver las ecuaciones reales.

Tabla 2. Ecuaciones de regresión del %BF basadas en el BMI que fueron utilizadas para realizar la validación cruzada en el estudio.

La absorciometría de rayos x de energía dual se seleccionó como metódo de referencia por su capacidad para evaluar la densidad mineral ósea, la cual puede variar en una población deportistas de sexo femenino (4,15,23). El equipamiento de DEXA que se usó en este estudio fue un GE Lunar Prodigy (Software versión 10,50,086, GE Lunar Corporation, Madison, WI) el cual fue comparado previamente con otro GE Lunar Prodigy y se observó una correlación fuerte (r = 0,99). Antes de cada día de evaluación el DEXA fue calibrado usando el bloque de calibración estándar del fabricante. Las participantes vistieron ropa sin metal (remera y short), y se les exigió que retiraran los objetos metálicos de su cuerpo y se quitaran los zapatos antes de cada medición. Durante el escaneo del DEXA, las participantes permanecieron en posición supina con los brazos a los costados y con las rodillas y los tobillos mantenidos juntos con correas de Velcro.  

Análisis Estadísticos 

Para determinar la diferencia entre el %BF obtenido por DEXA y el obtenido mediante las tres ecuaciones de %BF basadas en el BMI-(es decir, JBMI-BF, GBMI-BF, DBMI-BF), se aplicó el análisis de varianza de mediciones repetidas (ANOVA). El test post hoc de Bonferroni se realizó a continuación para establecer con más detalle las diferencias grupales en los valores de %BF. Además se construyeron los gráficos de Bland-Altman para identificar los límites de concordancia entre los valores de referencia y los valores estimados (3). Para las tres ecuaciones de estimación también se calcularon los valores del coeficiente de correlación producto-momento de Pearson, del error constante (CE), del error estándar de estimación (SEE) y del error total (TE). La significancia estadística fue fijada a priori en P <0,05, excepto en el análisis post hoc de Bonferroni en donde fue ajustada a P <0,008. Todos los análisis estadísticos fueron realizados con el software SPSS versión 16,0.

RESULTADOS

No se observaron diferencias significativas entre los cuatro deportes en el porcentaje de grasa corporal (%BF). Por lo tanto, las participantes fueron analizadas como un grupo entero. En la Tabla 3 se presentan las estadísticas de validez de estimar %BF a través de las ecuaciones de regresión BMI-%BF en comparación con el DEXA. El ANOVA de mediciones repetidas, indicó la existencia de diferencias significativas en los valores del %BF entre el DEXA y las ecuaciones de BF % basadas en el BMI (P <0,05). El análisis de seguimiento (post hoc) demostró que no había ninguna diferencia significativa entre la media de la medición de referencia (DEXA) y la media de JBMI-BF y DBMI-BF (P> 0,008). Sin embargo, el BF % estimado por GBMI-BF fue significativamente superior al determinado por DEXA (P <0,008). Así, el estadístico CE sólo fue significativamente diferente en GBMI-BF comparado con la medición de referencia. Se encontraron valores similares para r, SEE y TE entre las tres  ecuaciones de regresión de %BF basadas en BMI-(Tabla 3).

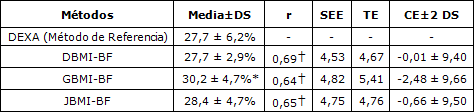
Tabla 3. Validación de la estimación del porcentaje de grasa corporal mediante ecuaciones de regresión de %BF basadas en el BMI en comparación con DEXA (n=75). DEXA = absorciometría de rayos x de energía dual; DBMI-BF = BMI-%BF ecuación de regresión de Deurenberg et al. (6); GBMI-BF = BMI-%BF ecuación de regresión de Gallagher et al. (10); JBMI-BF = BMI-%BF ecuación de regresión de Jackson et al. (13); r = Coeficiente de correlación producto-momento de Pearson; SEE = error estándar de la estimación; TE =  error total; CE = error/sesgo constante. * Presenta diferencias significativas con la medición por DEXA, p< 0,008. † Presenta una correlación significativa con la medición obtenida con DEXA, p< 0,05.

Los diagramas de puntos de Bland-Altman construidos para analizar las diferencias individuales entre la medición de referencia y las estimaciones del %BF se presentan en las Figuras 1 a 3. El sesgo medio estimado para el JBMI-BF fue -0,1% y el SD de ± 1,96 tomó valores de -10,3% a 8,9% (Figura 1). El sesgo medio para el GBMI-BF fue el mayor, ubicándose en -2,5% y tomando valores que iban de -12,1% a 7,1% (± 1,96 SD) (Figura 2). El sesgo medio para DBMI-BF fue el menor, ubicándose en 0,0% y tomando valores de -9,4% a 9,4% (± 1,96 SD) (Figura 3).

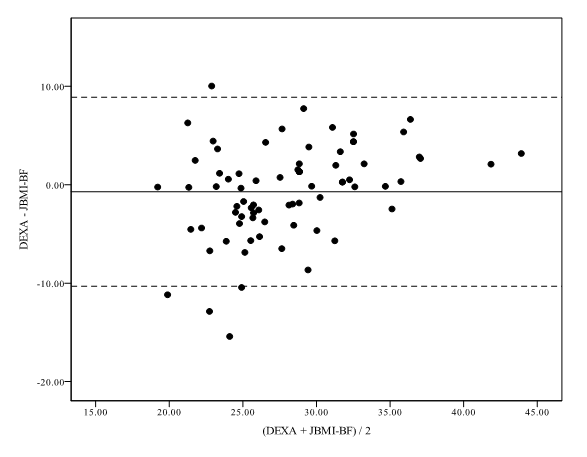
Figura 1. Diagrama de puntos de Bland Altman en el cual se compara el %BF estimado por JBMI-BF  con el valor de referencia (DEXA). La línea media indica la diferencia media entre el valor estimado y el valor real del %BF, las dos líneas punteadas externas indican la desviación estándar ± 1,96 ( ± 1,96 SD) de la diferencia

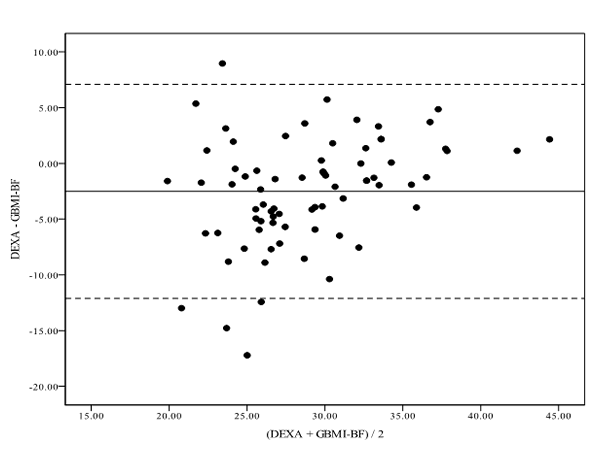
Figura 2. Diagrama de puntos de Bland Altman en el cual se compara el %BF estimado por GBMI-BF con el valor de referencia (DEXA). La línea media indica la diferencia media entre el valor estimado y el valor real del %BF, las dos líneas punteadas externas indican la desviación estándar ± 1,96 ( ± 1,96 SD) de la diferencia

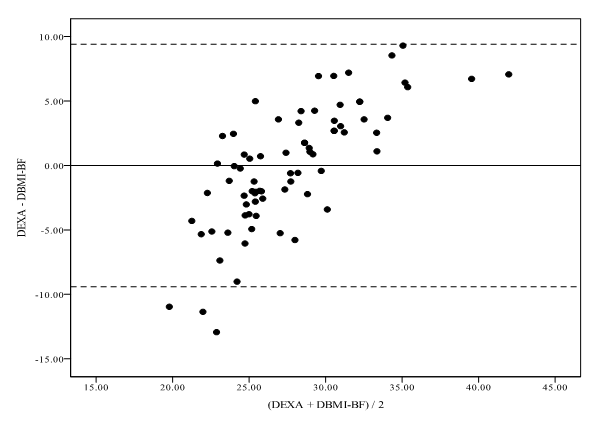
Figura 3. Diagramas de puntos de Bland-Altman en los cuales se presenta la comparación del %BF estimado por DBMI-BF con el método de referencia (DEXA). La línea media indica la diferencia media entre los valores del BF % estimados y los reales; las dos líneas punteadas exteriores indican el DS de ±1,96 de la diferencia.

DISCUSIÓN

Debido a que los atletas típicamente poseen mayor masa muscular en cualquier BMI dada, en comparación con quienes no son atletas (19), nuestra hipótesis fue que las ecuaciones de %BF basadas en el BMI no serían una técnica exacta comparada con DEXA, para estimar %BF en atletas de sexo femenino. Las ecuaciones de DBMI-BF, GBMI-BF y de JBMI-BF fueron establecidas por Deurenberg et al. (6), Gallagher et al. (9), Jackson et al. (11), respectivamente y fueron validadas en muestras grandes de la población adulta general. Estos estudios al efectuar comparaciones con los valores de referencia de DEXA (9) y del pesaje hidrostático (6,11), no observaron diferencias con las ecuaciones de estimación de %BF basadas en el BMI en las medias informadas para la población general.   

Nuestros resultados fueron similares, lo que demostró que no había ninguna diferencia significativa (es decir, JBMI-BF y DBMI-BF) o había pequeñas diferencias significativas (es decir, GBMI-BF) en los valores medios del BF % entre el DEXA y las ecuaciones de %BF basadas en el BMI en la cohorte completa de atletas femeninas. El CE/sesgo sólo presentó diferencias significativas entre la ecuación GBMI-BF y DEXA. Así, las ecuaciones de BMI de JBMI-BF y DBMI-BF pueden ser aceptables para obtener el %BF medio en un grupo completo de atletas femeninas. Sin embargo, el SEE y los valores de TE fueron bastante grandes para cada una de las tres ecuaciones de regresión (yendo de 4,53 a 4,82% y 4,67 a 5,41%, respectivamente). Además, los límites de concordancia entre los valores estimados y los del criterio de referencia, también eran grandes lo que es fácilmente observable al analizar las Figura 1 a 3. Los gráficos de puntos de Bland-Altman demostraron que JBMI-BF puede estar 10,3% por encima a 8,9% por debajo del DEXA, el GBMI-BF puede estar 12,1% por encima a 7,1% por debajo del DEXA y el DBMI-BF puede estar 9,4% por encima y 9,4% por debajo del DEXA. Parecería que cuando se evaluaba el %BF individual, las ecuaciones basadas en el BMI pueden clasificar erróneamente a sujetos con BF % saludable dentro de la categoría sobrepeso, o a sujetos que realmente tenían sobrepeso como saludables. Por consiguiente, el uso de las ecuaciones para estimar el %BF individual sobre la base del BMI, para atletas de sexo femenino es inaceptable y no recomendable. 

Se ha demostrado que atletas tienen niveles de %BF significativamente menores que sujetos con el mismo BMI que no son deportistas (19,24). En una muestra grande de atletas universitarios varones y mujeres, el BMI solo (es decir, cuando no se utilizaba en un modelo de estimación del %BF) frecuentemente clasificaba de manera errónea dentro de sobrepeso, a los sujetos que tenían grandes masas musculares pero mediciones de pliegues cutáneos de poco espesor (24). Nevill y colegas (18) reportaron resultados similares, lo que demuestra que en cualquier BMI dado, los atletas tenían un espesor de pliegues cutáneos mas bajo que el de sus pares que no eran atletas. En un estudio realizado por Ode et al., (19) se demostró que los puntos de corte de BMI/%BF establecidos por Gallagher et al. (9) clasifican al 31% de las atletas femeninas que tienen un %BF normal (es decir, %BF <33%) dentro de la categoría sobrepeso (es decir, BMI> 25 kg·m^-2) en comparación con sólo 7% de las mujeres que no son deportistas. Además, 77% de las atletas mujeres con un BMI mayor a 25 kg·m^-2 eran clasificadas dentro del peso normal (19). Por lo tanto, dudamos que el BMI utilizado solo, refleje con precisión la adiposidad en con gran contenido de masa magra.   

Otros estudios han realizado la validación cruzada de la ecuación de BMI-%BF en la población general. En comparación con el pesaje hidrostático, la ecuación de BMI-%BF de Deurenburg et al. (6) subestimó significativamente el %BF en 3,4% en mujeres jóvenes-adultas (21). Otro estudio efectuó la comparación de la misma ecuación con las mediciones de referencia por DEXA y pesaje hidrostático (5). Los autores concluyeron que el %BF estimado a partir del BMI es válido en ese nivel poblacional (5). Sin embargo, el SEE y los límites de concordancia entre la ecuación BMI-%BF y las mediciones de referencia para las mujeres en su estudio (5) eran similares a los del estudio presente.  

Los resultados del presente estudio, sugieren que existe una variación considerable en el %BF real en cualquier BF % estimado a partir del BMI. Los atletas típicamente tienen más masa muscular que la población general, que no realiza deportes. Una deportista con mucha masa muscular puede tener un BMI alto, aunque su %BF real puede ser bajo. En este caso, cualquier ecuación de %BF basada en el BMI podría sobreestimar mucho el %BF. Así, este estudio sugiere que muchas deportistas serán clasificadas de manera errónea como gordas/con sobrepeso, si se utiliza el BMI como un sustituto del %BF real, lo que concuerda con investigaciones previas que analizaron el BMI solo (19,20). Estas ecuaciones no deben ser utilizadas como un estimador del %BF individual en mujeres deportistas.   

El uso de DEXA como variable de referencia puede ser considerado una limitación dentro del estudio. Nosotros escogimos DEXA como método de referencia porque se ha sugerido previamente que puede ser apropiado para investigaciones de composición corporal que involucren a mujeres deportistas debido a la variación en la densidad mineral ósea (23). Sin embargo, las investigaciones actuales defienden el uso de modelo multi-compartimiento como método de referencia en los estudios de validación. Moon et al. (14) compararon DEXA, pesaje hidrostático y pletismografía de desplazamiento aéreo con un modelo multi-compartimiento en atetas de sexo femenino de la I División de NCAA. Los resultados demostraron que DEXA producía el error constante más grande (-3,71%), el error total más grande (4,90%) y tenía los mayores límites de concordancia (-10,10 a 2,68%) (14). Se necesitan mas investigaciones para comparar las ecuaciones de regresión de %BF basadas en el BMI con los modelos multi-compartimiento de %BF en deportistas de sexo femenino y en otras poblaciones. 

Conclusiones

La presente investigación buscó determinar si las ecuaciones de %BF basadas en el BMI eran una forma precisa de estimar el %BF en mujeres deportistas. Nuestros resultados demostraron que, o no había diferencia significativa (JBMI-BF, DBMI-BF) o solo había una pequeña diferencia significativa (GBMI-BF) cuando se comparaban las medias grupales entre las ecuaciones basadas en el BMI-y la metodología de diferencia, DEXA. Por lo tanto, para estimar el %BF en un grupo entero de atletas (es decir, al estimar el %BF promedio de un equipo), es aceptable el uso de las tres ecuaciones que se examinaron en este estudio. Sin embargo, debido al gran valor del error total (TE), del SEE y de los límites de concordancia, no se recomienda utilizar estas ecuaciones para estimar el %BF de atletas femeninas de manera individual. Los resultados demostraron que cada ecuación proporcionó valores muy por encima o por debajo del valor de %BF arrojado por la medición de referencia  Así, las ecuaciones de %BF basadas en el BMI para estimar el %BF individual para esta población, deben ser utilizadas con cuidado extremo o no ser utilizadas. Dado que las deportistas mujeres tienen un mayor riesgo de padecer desórdenes nutricionales y de imagen corporal (17,22), la clasificación errónea de una deportista dentro de una categoría con sobrepeso o con peso insuficiente, podría tener importantes riesgos para la salud.   

Dirección para Envío de Correspondencia

Esco MR, PhD, Auburn University Montgomery, Department of Physical Education and Exercise Science/Human Performance Laboratory, P.O. Box 244023,Montgomery, AL, USA, 36124-4023. (334) 244-3161, (334) 244-3198; Correo electrónico: mesco@aum.edu