Validación de un Modelo de Clasificación para Carreras de 5 km en Base a la Edad y al Peso Corporal

Aunque el aumento en la edad y en el peso corporal (BW) ha sido asociado ampliamente con mayores tiempos en carreras de distancia, la convención más común en las carreras de 5 km es clasificar a los competidores según la edad y, en ciertas ocasiones, por el BW. Esto tiene la desventaja de clasificar a pequeños números de competidores en categorías de edad, dándoles ventaja a aquellos corredores que se encuentran próximos a la edad mínima o al mínimo valor de BW disponible. Utilizando los recientes avances en los modelos de rendimiento de carrera con el BW en combinación con la evidencia empírica que ha cuantificado el efecto independiente de la edad sobre la resistencia cardiovascular, recientemente hemos publicado la derivación del índice 5K (5KH), un modelo de clasificación basado en la edad y el BW para la carrera de 5 km. Ingresando los valores de edad, BW y el tiempo real de carrera, el 5KH calcula un tiempo ajustado de carrera que puede ser utilizado para comparar corredores de diferentes edades y BW dentro del mismo sexo. En este estudio, hemos realizado la evaluación de campo del 5KH en dos carreras locales con 275 hombres y 126 mujeres. Los resultados sugieren que el 5KH elimina los sesgos provocados por la edad y el BW, y que puede proveer un mayor incentivo para que los corredores de mayor edad y peso corporal participen en las competiciones. Además, el sesgo provocado por el BW en las carreras de 5 km tiende a ser menor para las mujeres que para los hombres. Siendo el primer sistema de clasificación basado científicamente en la edad y el BW, el 5KH parece ser un sistema válido para ambos sexos y podría tener aplicación en otras distancias de carrera y en la evaluación de la aptitud física.

INTRODUCCION

Si bien existen muchos factores que contribuyen al rendimiento en las carreras de distancia, se ha aceptado ampliamente la idea de que el aumento en la edad y el peso corporal (BW) contribuyen a los mayores tiempos observados en estas carreras. Casi todas las carreras tienen categorías de edad, y en ciertos casos, divisiones por BW. La principal limitación de la categorización por edades (e.g., 50-54, 55-59, 60-64, etc.) es que con frecuencia hay muy pocos competidores en las categorías de mayor edad, y algunas veces hay menos competidores que premios. Cuando se utiliza la categorización por BW, comúnmente se agregan solo una o dos categorías para los sujetos con mayor BW, de manera tal que los corredores que se encuentren por encima del BW mínimo (el menor BW permitido para cada categoría) puedan competir entre si. Las divisiones (www.clydesdale.org) denominadas “Clydesdale” para los hombres y “Fillies” para las mujeres, se dividen en Clydesdale A: 200–225 lbs (90.7–102.0 kg), Clydesdale B: 225+lbs (102+kg), y Fillies: 150+lbs (68.0+kg). Las limitaciones de la categorización por edad y/o BW pueden ser mitigadas utilizando un sistema de categorización que clasifique de forma más precisa la edad y el BW como variables continuas. Utilizando los recientes avances en los modelos de rendimiento de carrera con el BW y la evidencia empírica que ha cuantificado el efecto independiente de la edad sobre la resistencia cardiovascular, recientemente hemos desarrollado el índice 5K (5KH), una ecuación que ajusta el tiempo de carrera real en 5 km al BW y la edad (1). Debido a que el eje de nuestro trabajo previo fue el cálculo del 5K, el eje de la presente investigación fue aplicar el modelo a una gran muestra de corredores hombres y mujeres para evaluar el grado en el cual eliminaba los sesgos de la edad y el BW.

Aunque los detalles del 5KH pueden encontrarse en nuestro artículo previo (1), el primer paso al desarrollar el 5KH fue modelar los efectos fisiológicos de la edad sobre el rendimiento en las carreras de fondo. Esto se llevó a cabo en base a dos relaciones clave: edad vs. consumo máximo de oxígeno (VO₂ máx.) para hombre y mujeres; y VO₂ máx. vs. tiempo de carrera. Utilizando muestras con gran número de sujetos, Jackson et al. (2, 3) cuantificaron el cambio en el VO₂máx. debido a la edad, independientemente del porcentaje de grasa corporal y de la actividad física realizada por los sujetos, como 0.25 y 0.26 ml de O₂/kg/año para hombres y mujeres, respectivamente. Combinando estos hallazgos con una ecuación desarrollada por Nevill (4), la cual vincula la velocidad durante la carrera de 5 km y el VO₂ máx., hemos calculado los efectos de la edad sobre los cambios en el tiempo durante la carrera de 5 km (1).

El segundo paso fue modelar el efecto fisiológico del BW sobre el rendimiento en las carreras de fondo. La combinación de la ecuación de Nevill (4), la cual también incluye el BW, y los hallazgos de Astrand y Rodahl (5), quienes propusieron que el VO₂ máx. debería ajustarse al BW elevado a una potencia de 2/3, llevaron a la conclusión de que el tiempo en las carreras de fondo debería ser proporcional al BW elevado a una potencia de 1/3 (1). Esta relación, la cual ha sido respaldada empíricamente (6, 7), significa que si un corredor realizara el ajuste de si mismo/misma al modelo pero con un peso 10% mayor (esto es lo mismo que multiplicar por 1.10) entonces su tiempo de carrera se debería incrementar en (1.10)1/3 o 1.0323 (un incremento del 3.23%). Si bien este ajuste relativo no parece ser significativo, este cambio se traduce en 39 segundos extra para una persona que corre los 5 km en 1200 segundos (20:00), lo cual podría claramente alterar su orden de llegada.

Los efectos de la edad y del BW sobre el tiempo de carrera fueron combinados en ecuaciones específicas del sexo como se ha reportado previamente (1). Ingresando el tiempo real registrado en carreras de 5 km (RT), la edad y el BW, la ecuación produce un tiempo de carrera ajustado (RTadj) el cual, a su vez, puede ser utilizado para comparar corredores de diferentes edades y BW. Sin embargo, debido a que la teoría subyacente se aplica a adultos físicamente maduros el modelo 5KH impone la utilización de una edad mínima de 25 años para hombres y mujeres y de un BW mínimo de 50 kg para las mujeres y de 65 kg para los hombres. Estos límites están basados en la edad promedio (25 años) para los corredores de 5000 m de elite (International Association of Athletics Federation, www.iaaf.org, Diciembre de 2005) y en el peso promedio de los corredores de clase mundial utilizados en estudios de investigación publicados con muestras de al menos 25 sujetos (8, 9). Por lo tanto el RTadj para sujetos menores de 25 años de edad o con pesos menores a 50 y 65 kg para mujeres y hombres respectivamente, se deriva utilizando la edad y el BW mínimo descritos anteriormente.

La Tabla 1 ilustra el efecto del modelo 5KH sobre cuatro corredores hipotéticos. El corredor A, que es menor, más liviano y más rápido que el corredor B, tiene un RTadj mayor debido a la clasificación vinculada con los efectos documentados de la edad y el BW. La Figura 1 muestra las instrucciones del 5KH, así como también un vínculo para cálculos vía Internet y un archivo con una hoja de cálculo para calcular múltiples tiempos RTadj.

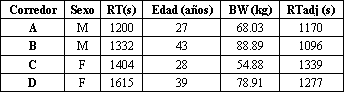
Tabla 1. Modelo 5KH para cuatro corredores hipotéticos. RT: tiempo real en la carrera de 5 km, BW: peso corporal, RTadj: el tiempo de carrera ajustado al modelo 5KH en base a la edad y el peso corporal.

Tabla 2. Reglas y sitio Web del modelo 5KH.

METODOS

Sujetos

Para validar el modelo 5KH en corredores que participan en eventos reales hemos aplicado el modelo 5KH a 275 hombres y 126 mujeres que compitieron en dos carreras de 5 km a nivel regional en el suroeste de Ohio. Los participantes del estudio eran corredores que participaron voluntariamente no solo en la carrera sino como sujetos para el modelo 5KH. Como tales, estos dieron su consentimiento por escrito para ambas participaciones y recibieron un breve resumen de los procedimientos del 5KH. Los sujetos fueron reclutados por medio de volantes, sitios Web dedicados a carreras, y/o en los mostradores de exhibición para el retiro de formularios (dos días antes) y en el sitio de registro el día de la carrera. La estadística descriptiva de los sujetos se muestra en la Tabla 3.

Tabla 3. Participantes del estudio de validación.

Procedimientos

Los participantes se reportaron tanto en los sitios para el retiro de formularios dos días antes de la carrera o en una estación de pesaje el día de la carrera en donde se ofrecieron como voluntarios para participar en el estudio de validación del 5KH. En cualquiera de los casos, los sujetos fueron pesados en una de tres balanzas digitales calibradas y el BW fue registrado con una precisión de ½ kg. Debido a restricciones temporales y a la capacidad de pesaje, hemos medido cada sujeto solo una vez con el mismo utilizando su vestimenta normal o un atuendo de carrera. Para aquellos que fueron pesados con su vestimenta normal, se realizó un ajuste de 1.5 kg para aproximar el BW al que tendrían con el atuendo de carrera. Ambas carreras se llevaron a cabo en terrenos planos con temperaturas que variaron entre los 14 y los 18 ºC.

Análisis Estadísticos

La clave métrica para evaluar la efectividad del modelo 5KH fue la eliminación de los sesgos de edad y BW en el RTadj. Para determinar la existencia de sesgos en el RT, para cada sexo, hemos calculado el índice r² para RT vs. edad y luego para el BW. Lo mismo se realizó para el RTadj vs. la edad y luego el BW. Estos datos fueron seleccionados sobre el RT a priori en base a nuestra suposición de que estos sujetos proveerían un indicador más preciso del esfuerzo relativo a través de diversos rangos de edades y BW. Nuestra hipótesis fue que, para ambos sexos y considerando submuestras de sujetos más veloces, las correlaciones se aproximarían a cero en la condición de RTadj, lo cual indicaría que los sesgos fueron eliminados.

RESULTADOS

Las Figuras 2 y 3 muestran los análisis de los sesgos para hombres y mujeres. Como se había hipotetizado, el modelo 5KH removió tanto el sesgo de la edad como el del BW, especialmente cuando se consideraron a los corredores más veloces. En otras palabras, entre aquellos que realmente corrieron (no caminaron o trotaron) durante la carrera, el sesgo de la edad y del BW contra los corredores de mayor peso corporal y de mayor edad, lo cual fue aparente con los valores de RT, fueron reducidos a casi cero en los valores de RTadj.

Se observaron varios fenómenos interesantes. Primero, para todas las mujeres (n=126), el modelo 5KH no pareció reducir el sesgo en la relación edad vs. RT, dado que el r² para la edad vs. RTadj fue estadísticamente significativo. Sin embargo, análisis similares llevados a cabo para las mujeres más veloces, con puntos límites de tiempo de 1560 y 1440 segundos, indicaron que la relación edad vs RT se vio fortalecida y que la relación edad vs RTadj fue reducida a casi cero. Debido a que la naturaleza de confusión de los esfuerzos submáximos, esto sugeriría que el ajuste del modelo 5KH por la edad en las mujeres fue válido. El análisis de los sesgos para los hombres sugirió claramente un correcto ajuste para la edad a través de todas las muestras. Segundo, cuando todas las mujeres (n=126) fueron consideradas, no se evidenciaron sesgos del BW en el valor de r² para la relación BW vs. RT. De esta manera, no fue sorprendente que el RTadj tuviera poco efecto. Esto normalmente podría sugerir que no existen sesgos del BW en la carrera de 5 km para mujeres. Sin embargo, análisis similares llevados a cabo con las mujeres más veloces indicaron sesgos del BW en el RT y que esencialmente no había sesgos del BW en el RTadj. Tercero, la fuerza de la relación BW vs. RT, el indicador clave del sesgo del BW en la carrera de 5 km, fue mayor para los hombres que para las mujeres, incluso entre los corredores más veloces.

Los comentarios anecdóticos realizados por los corredores fueron en general bastante positivos. Muchos participantes expresaron su apreciación por la idea general, al ser reconocidos como mejores corredores de lo que habían sido reconocidos en el pasado, y tenían la esperanza de que esta clasificación fuera utilizada en futuras carreras. El único comentario negativo provino de algunas mujeres que no deseaban ser pesadas. Esto puedo apreciarse por la menor cantidad de mujeres que participaron en el 5KH, en las dos carreras, en comparación con los hombres, a pesar de la casi paridad global en los sexos. Otra potencial limitación fue la capacidad de pesaje.

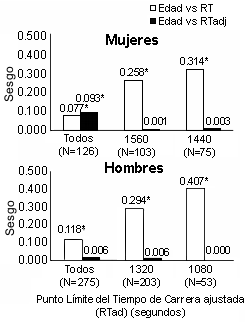
Figura 1. Análisis del sesgo de la edad para el modelo 5KH. El sesgo fue definido como el valor del índice r² de Pearson entre la edad y el tiempo real de carrera (RT) o el tiempo de carrera ajustado (RTadj). *p<0.05.

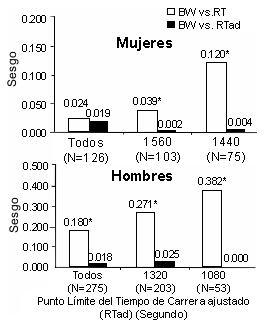
Figura 2. Análisis del sesgo del peso corporal (BW) para el modelo 5KH. El sesgo fue definido como el valor del índice r² de Pearson entre la edad y el tiempo real de carrera (RT) o el tiempo de carrera ajustado (RTadj). *p<0.05.

DISCUSION

El modelo 5KH parece eliminar los sesgos de la edad y el BW asociados con el tiempo de carrera en 5 km tanto para los hombres como para las mujeres. La consideración de submuestras de corredores más veloces en ambos sexos indicó que había mayores sesgos para el RT y que esencialmente no existían sesgos para el RTadj. Sin embargo, la tendencia hacia un menor valor de r² en la relación BW vs. RT en las mujeres no puede ser explicada con los presentes datos, pero puede relacionarse con diferencias sexuales en el esfuerzo y/o en el porcentaje de grasa corporal. Por esta razón recomendamos que esto sea investigada en futuros estudios.

Si bien el calculador del sitio Web del 5KH referenciado en la Tabla 2 es fácil de utilizar, se deberían resaltar varios procedimientos importantes y aspectos relacionados con el manejo de datos. Primero, pueden participar corredores de cualquier edad y BW. Sin embargo, los corredores más jóvenes y más livianos pueden no obtener un puntaje de clasificación, por lo que su RTadj será igual a su RT. Los adultos jóvenes de mayor peso y los adultos mayores de menor peso serán clasificados, pero el valor obtenido puede estar basado solo en el BW para los primeros y en la edad para los segundos. Segundo, la utilización del 5KH puede hacer que se incremente la estructura de premios existentes en cualquier carrera. De hecho, recomendamos la utilización del 5KH además de todos los otros premios de manera que se maximice la oportunidad de que los corredores sean premiados. En nuestras dos carreras más recientes, ofrecimos premios a los primeros cinco hombres y mujeres del 5KH además de los otros premios estándar (e.g., categoría abierta, gurpo A, Clydesdale/Filly). Los únicos corredores no elegibles para los premios 5KH fueron los hombres y mujeres que finalizaron entre los primeros tres puestos en la general. Sorprendentemente, pocos recibieron múltiples premios. Tercero, debido a que el 5KH utiliza valores de tiempo que no son propicios para ecuaciones matemáticas simples y debido a que las ecuaciones son bastante extensas (la Ref. 1 contiene todas las ecuaciones para los hombres y mujeres), estimulamos la utilización de las hojas de cálculo para múltiples corredores o el calculador del sitio Web para individuos (Tabla 2).

Algunos podrían pensar que al ofrecer una clasificación por BW, el 5KH puede premiar el exceso de grasa corporal, lo cual provoca el bien documentado efecto de una menor velocidad de carrera y de un mayor gasto energético a una velocidad de carrera dada (10). Un breve análisis de dos casos hipotéticos muestra que el 5KH no premia el incremento en la grasa corporal. Primero, una mujer de 45 años de edad y 69.8 kg con un tiempo de carrera de 1800 segundos (30:00) tendría un RTadj de 1417 segundos (23:37). Si esta mujer ganara 1.8 kg de grasa adicional, sin cambios en su capacidad aeróbica, entonces la ecuación de Nevill (4) predeciría que esta mujer tendría un RT de 1853 segundos (30:53), debido a que su exceso de BW la haría más lenta. Esto hace que su nuevo RTadj sea de 1441 segundos (24:01), un RTadj 24 segundos mayor. El escenario más probable es que su capacidad aeróbica se reduzca con la ganancia de grasa corporal contribuyendo con una penalidad de más de 24 segundos. En resumen, la ganancia de grasa corporal no parece ser premiada por el 5KH.

Como segundo ejemplo, dos hombres, ambos de 55 años de edad, que corren con el mismo tiempo de 1560 segundos (26:00), tienen BW de 95.2 y 102.0 kg, tal que la diferencia en el BW se deba solo a un exceso de grasa corporal. Su RTadj sería de 1160 segundos (19:20) y 1134 segundos (18:54) para el corredor de menor y mayor peso, respectivamente. Si bien se podría concluir que el exceso de grasa corporal está siendo premiado, un análisis más profundo revela que esto no es así. El exceso de grasa del corredor de mayor peso no es distinto de un chaleco de pesas. Si estos dos corredores tuvieran el mismo BW, y uno tuviera que llevar un chaleco que pese 6.8 kg, y ambos corrieran la distancia en 1560 segundos (26:00), entonces el corredor que lleva el chaleco sería considerado “ganador” por cualquier estándar ya que su nivel de aptitud física es mayor. Además, si el corredor de mayor peso perdiera 6.8 kg de grasa corporal, sin cambios en su capacidad aeróbica, entonces su nuevo RT, utilizando el mismo análisis que se utilizó para el ejemplo de la mujer, sería de 1454 segundos (24:14) y su RTadj sería de 1093 (18:13), una mejora de 41 segundos. Además, con dicha pérdida de grasa corporal es probable que su capacidad aeróbica mejore, reduciendo su RT real, y contribuyendo de esta manera a una mejora de más de 41 segundos. Nuevamente, la pérdida de grasa corporal debería ser ventajosa para el 5KH.

Hemos recibido cuestionamientos de corredores y científicos del ejercicio acerca de porque ni la talla ni el índice de masa corporal (BMI: peso/talla²) fueron utilizados en el 5KH. Primero, sabemos que no existen datos empíricos que hayan examinado la relación entre el BMI o la talla y el rendimiento en carreras de fondo. Segundo, ninguna investigación publicada ha realizado modelos que incluyeran la talla o el BMI para las carreras de fondo. El BW, como se discutiera previamente, se ajusta adecuadamente a los criterios de inclusión y ha sido utilizado y validado en otros eventos competitivos incluyendo en aquellos acerca de la fuerza muscular (11). Sin embargo, creemos que los estudios futuros deberían examinar la clasificación según la talla, dadas nuestras observaciones acerca de la renuencia por parte de algunas mujeres a ser pesadas.

Nuestro grupo está actualmente investigando los métodos de aplicar el concepto del 5KH a las carreras de 10 km, media maratón y maratón completa. Si bien la simplicidad de aproximar los factores de ajuste es atractiva, debemos ser conscientes de que la fisiología de la carrera de fondo es diferente en las carreras de mayor distancia, particularmente con respecto a la utilización de sustratos, reservas de glucógeno y a la capacidad de regulación de la temperatura. Por lo tanto, no tenemos claro en que forma podrían cambiar estos factores nuestras suposiciones en las cuales esta basado el 5KH. No obstante, creemos que sistemas similares de clasificación para las carreras de distancias mayores son objetivos valiosos.

Conclusiones

El 5KH parece ser válido tanto para hombres y mujeres en cuanto elimina los sesgos de edad y BW presentes en una carrera de 5 km. Esto es especialmente verdadero cuando se consideran los corredores más veloces. Además, el sesgo del BW en las carreras de 5 km parece ser mayor para los hombres que para las mujeres por razones que no pueden ser dilucidadas en el presente estudio. Por último, el 5HK parece premiar la pérdida de grasa corporal y penalizar la ganancia de grasa corporal. En el sitio Web se encuentra disponible un calculador y una hoja de cálculo que puede descargarse para realizar cómputos de únicas y/o múltiples puntuaciones de forma rápida y con un marco amigable para el usuario. Los organizadores de carreras deberían considerar la logística para el pesaje de los corredores interesados, especialmente mujeres, quienes parecen menos dispuestas a ser pesadas que los hombres. Por último, recomendamos estudiar adicionalmente las diferencias sexuales observadas respecto del sesgo del BW así como también la validación de esta aproximación con carreras de 10 km, ½ maratón y maratón.

Dirección para el Envío de Correspondencia

Vanderburgh PM, EdD, Department of Health and Sport Science, University of Dayton, Dayton, OH, 45469-1210. Teléfono: (937) 229-4213; Fax: (937) 229-424; correo electrónico: vanderburgh@udayton.edu.