Departamento de fundamentos de la motricidad y entrenamiento deportivo. Univ. Europea de Madrid (UEM).
Resumen
INTRODUCCION
La capacidad de aplicar fuerza con la máxima velocidad posible determina los niveles de potencia muscular, la cual ha sido considerada como un indicador clave de la intensidad de esfuerzos físicos (Cronin and Sleivert, 2005, Graham, 2002). Este parámetro, junto con la relación determinada entre la fuerza y la velocidad en distintos ejercicios, han sido utilizados para describir las características funcionales, así como los efectos de los entrenamientos aplicados en diferentes actividades deportivas (Baker, 2001, Naclerio et al., 2007)
De acuerdo a los estudios de H.V. Hill al establecer la relación entre fuerza y velocidad en un laboratorio con preparados de músculos aislados, los valores más altos de potencia se alcanzan sobre el 35-40% de la fuerza máxima isométrica y entre el 35-45% de la máxima velocidad de acortamiento muscular. No obstante, cuando esta relación es analizada durante ejercicios in vivo, como la carrera, los saltos o los lanzamientos, la forma en que estas dos variables se relacionan y los porcentajes de peso respecto de los valores máximos en donde se producen las potencias más elevadas varían, incluso entre diferentes técnicas de ejercicios (Cronin and Sleivert, 2005, Naclerio, 2006, Naclerio, 2007). De todas maneras, diversos estudios realizados con deportistas han mostrado que al realizar saltos verticales las potencias máximas se logran al saltar sin sobrecarga (con el propio peso corporal), siendo posible estimar la relación entre fuerza y velocidad en la musculatura extensora del tren inferior realizando saltos con pesos crecientes (Bosco, 1983, Bosco, 1990, Bosco, 1992, Sale, 1991). Esta metodología, ha sido aplicada ejecutando movimientos veloces sin llegar a saltar (sentadilla) o con saltos verticales incrementando la resistencia por medio de pesos externos comprendidos entre 10 y 70 o 100 kg (Hakkinen et al., 1984, Rahmani et al., 2002, Bosco, 1992) o determinando la cantidad de los pesos con relación al peso corporal de cada sujeto (Bosco et al., 1982, Bosco, 1992). Respecto a este último criterio, Bosco (1992), indica que la relación entre la fuerza y velocidad producida en gestos balísticos puede ser estimada por el cociente entre la altura alcanzada en un salto con una sobrecarga externa similar al peso corporal y otro sin sobrecarga externa (sólo con el propio peso corporal) (índice de Bosco). Debido a que la altura de un salto vertical se relaciona significativamente con la velocidad vertical al momento del despegue, la altura alcanzada en el primer salto sin sobrecarga (SJ) en donde el sujeto moviliza sólo su propio peso corporal (menor resistencia posible), se relaciona con la máxima velocidad de acortamiento muscular, mientras que en el salto con sobrecarga externa (SJ + kg pc), el peso a vencer se duplica y la altura alcanzada dependerá en mayor medida de los niveles de fuerza máxima. Según Bosco (1992), el índice resultante de la relación (SJ + kg pc) / SJ, refleja el equilibrio entre las capacidades de fuerza y velocidad del tren inferior transformándose en un indicador de los efectos de los entrenamientos aplicados. Por ejemplo, un sujeto que tenga un SJ+kg pc = 0.15 m y un SJ = 0.45, tendrá un índice de 0.33, es decir que cuando salta con un peso externo similar el peso corporal logra el 33% de la altura alcanzada sin sobrecarga. Según Bosco (1992), los efectos del entrenamiento pueden controlarse comparando los valores de este índice con los valores de referencia indicados para cada especialidad deportiva y que este autor publica en el capitulo 6 paginas 123 a 170 (Bosco, 1992). De esta manera, si el sujeto mencionado anteriormente tuviese un índice de referencia superior a 0.33, debería orientar su entrenamiento hacia las acciones veloces y de explosividad de modo de incrementar la capacidad de salto con cargas bajas, sin necesidad de modificar el rendimiento con las cargas más altas. Por el contrario, si el índice de referencia fuese mayor, debería entrenar con cargas más altas haciendo hincapié en la fuerza de modo de mejorar el rendimiento con los pesos más elevados y no tanto con los pesos bajos.
Aunque en una primera instancia, los criterios expresados por Bosco (1992), puedan parecer coherentes, el autor del presente estudio considera que carecen de un fundamento fisiológico sólido, ya que la capacidad de realizar una acción explosiva o balística como un salto dependen principalmente del nivel de sobrecarga movilizado (Verkhoshansky, 1996), siendo especialmente importante para los saltos verticales la relación establecida entre el peso corporal y el nivel de la 1 MR determinado en un ejercicio mecánicamente similar. Esta relación indica el porcentaje de peso que representa el peso corporal de cada sujeto respecto de su fuerza máxima, y además de determinar el tipo de fuerza aplicado (explosiva, potencia o máxima) (Naclerio, 2005, Naclerio and Jiménez, 2005) indica el porcentaje mínimo de peso que va ser movilizado al inicio del test de saltos con pesos. De todos modos, muy pocas veces se ha establecido esta relación considerando las sobrecargas con relación al porcentaje de la 1 MR.
Kellis et al., (2005), evaluaron a un grupo de estudiantes varones, que realizaron un test progresivo en sentadilla paralela, aplicando pesos de entre 10 y 100 kg que posteriormente fueron relacionados con el 7% y el 70% del nivel de la 1 MR. Estos autores, observaron que los valores más altos de potencia y velocidad se alcanzaban entre el 7% y el 14% de la 1MR siendo estos significativamente diferentes (p<0.05) respecto de los producidos con pesos superiores al 14%. De todos modos, en este trabajo se calculó la 1 MR considerando sólo la sobrecarga externa, sin incluir el peso corporal como parte de la carga movilizada. Este error, aunque no influyo en los cálculos de la fuerza (N) o la potencia (W), porque se utilizó una plataforma dinamométrica, si puede haber influido sobe las recomendaciones realizadas respecto de los porcentajes de peso en donde se alcanzan los valores más altos de potencia y por lo tanto debería ser considerado cuando otros entrenadores o investigadores realicen test similares pero utilizando otro tipo de tecnología como los transductores de velocidad o las plataformas de contacto, en donde la inclusión o no del peso corporal puede afectar no solo la relación porcentual sino también los cálculos de la potencia mecánica (Cormie et al., 2007).
Viitasalo, (1985), indica que el test de saltos verticales utilizando una plataforma de contacto en donde la velocidad de desplazamiento angular de la rodilla se relaciona con tiempo de vuelo que permite posteriormente calcular la altura del salto, mientras que la fuerza se estima por el peso total movilizado (peso corporal más la sobrecarga externa en kg), constituye una metodología fiable para estimar la relación fuerza-velocidad en los saltos verticales. No obstante, aunque en diversos estudios se han estandarizado los procedimientos para realizar este test (Sale, 1991), el mismo nunca se ha efectuado considerando el nivel de sobrecarga respecto al valor de 1 MR, ni controlando el rango de desplazamiento angular para que sean iguales en los saltos y en la sentadilla (que indica el nivel de 1 MR o 100%). Debido a esto, es posible que muchos resultados o indicaciones respecto al nivel de la sobrecarga elegida para el entrenamiento no se adecuen al rendimiento real de cada sujeto.
Para poder aclarar estos aspectos metodológicos relacionados con la aplicación del test de saltos con pesos, en la Universidad Europea de Madrid, realizamos un estudio cuyo objetivo fue analizar las diferencias entre las alturas o potencias producidas al saltar con distintos porcentajes de la 1 MR obtenida en un ejercicio mecánicamente similar. Los sujetos de este estudio fueron 14 varones voluntarios (28.7±3.5 años, 177.9±9.6 cm y 76.35±7.3 kg), pertenecientes a diferentes especialidades deportivas: 8 aspirantes a entrar en el cuerpo de bomberos de la comunidad de Madrid, 2 jugadores de baloncesto de nivel regional, 2 esquiadores de slalom de nivel Nacional, 1 competidor de aeróbic de nivel Nacional y 1 judoka de nivel internacional.
EVALUACIONES
Se realizaron dos tests separados con 48 hs de descanso:
- Test de 1 MR en sentadilla con barra libre, llegando hasta una angulación de 90º en la articulación de la rodilla y apoyando la barra sobre la 7º vértebra cervical (Wretmeberg et al., 1996). En este ejercicio, el valor de la 1 MR en kg totales fue determinado por la suma del peso externo movilizado y el 90% del peso corporal de cada sujeto (Dugan et al., 2004, Cormie et al., 2007).
- Test de saltos con pesos crecientes sobre una plataforma de contacto (Globus Italia), siguiendo el protocolo similar al descrito por Viitasalo (1985), pero estableciendo el nivel de sobrecarga en base al porcentaje de la 1 MR determinado previamente en la sentadilla. De esta manera, salvo en el primer salto que se realizaba sin sobrecarga externa ya que el porcentaje estaba determinado por la relación entre el peso corporal/1MR, en los demás saltos el nivel de sobrecarga debía estar comprendido dentro de los siguientes rangos porcentuales: 41% a 50% en el 2º salto, 51% a 60% en el 3º, 61 a 70% en el 4º, 71 a 80% en el 5º, 81 a 90% en el 6º y más del 90% en el 7º. Aunque este test comprendía la realización de 7 saltos, la prueba se detenía en cuanto los sujetos no podían despegar los pies de la plataforma, es decir si no se detectaba fase de vuelo. Por otro lado, la técnica de ejecución de los saltos se realizaba guardando la mayor similitud posible con el ejercicio de sentadilla evaluado previamente. De esta manera, se controló la fase de descenso y grado de flexión de rodillas hasta 90º, colocando un banco que delimitase y obligase a los sujetos a respetar este rango de desplazamiento durante la fase de descenso del CMJ en donde un evaluador indicaba el momento en que los sujetos debían invertir la dirección del movimiento.
La altura del salto fue calculada a partir del tiempo de vuelo medido por la plataforma de contacto y aplicando la metodología descripta por Komi y Bosco (1978).
El pico de potencia fue calculado por la fórmula propuesta por Sayers y col, (1999) en donde la potencia pico (Vatios) = 60.7 (altura del salto en cm) + 43.5 (peso corporal en kg)–2055.
RESULTADOS
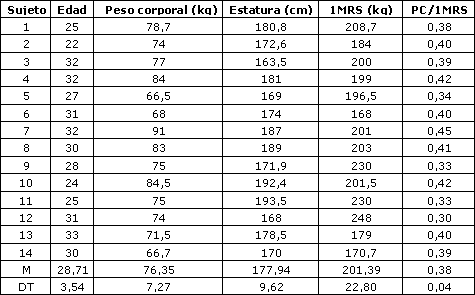
En la Tabla 1, se describen los resultados de los 14 sujetos evaluados, así como la media (M) y la desviación típica (DT) de las variables biométricas, el nivel de la 1 MR en sentadilla y el cociente entre el peso corporal (PC) /1MRS.
Tabla 1. Valores medidos en cada sujeto, M y DT obtenido en las variables biométricas y la sentadilla con barra libre (SBL).
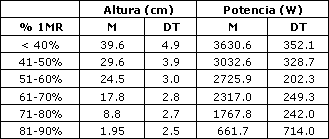
La Tabla 2 y la Figura 1, muestran los valores medios (M) y de desviación típica (DT) de las alturas y potencias alcanzadas en el test de saltos verticales con pesos crecientes.
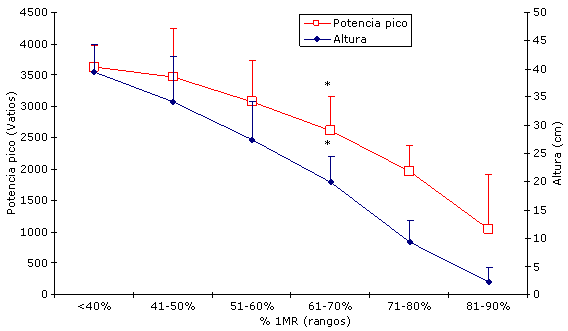
En la Figura 1, se observa como las alturas y potencias producidas con los pesos más bajos (<40%) son diferentes (p<0.05) respecto de las logradas con porcentajes superiores al 60% de la 1 MR. Por otro lado los saltos realizados con el 41-50 y 51-60% de la 1MR son significativamente más altos y potentes respecto de los ejecutados con el 71-80% y 81-90%, respectivamente. Además es importante destacar que ningún sujeto fue capaz de saltar con porcentajes mayores del 90% de la 1MR.
Tabla 2. M y DS de los resultados obtenidos en el test de saltos con pesos crecientes
Figura 1. Valores medios y DT de la altura y la potencia calculadas en los diferentes porcentajes evaluados en cada salto. * p<0.05: Diferencias significativas con respecto a la altura o la potencia alcanzada con <40%. δ p<0.05: Diferencias significativas con respecto de las alturas o potencias producidas con el 41-50%. ß p< 0.05: Diferencias significativas con respecto de las alturas o potencias producidas al 51-60%
La potencia pico, describe una curva descendente, similar a la de la altura, y aunque no se observan diferencias significativas entre los primeros tres rangos porcentuales (p>0.05), ya con el 2º rango (41 al 50%) se produce una caída mayor del 10% y con el 3º rango (51 al 60%) una pérdida superior al 20%, respecto de la máxima potencia alcanzada con <40% de la 1 MR.
DISCUSION
Los resultados de este estudio, indican que al saltar con porcentajes de peso bajos (<40%), la altura y la potencia alcanzada son significativamente más altas respecto de las producidos con porcentajes medios o altos (>60%). Por otro lado, a pesar de no observarse diferencias significativas, el pico de potencia cae más de un 10% al saltar sobrecargas mayores del 40% de la 1 MR y más de un 20% con peso comprendidos entre el 51 y el 60% de la 1 MR. Este comportamiento, es similar aunque algo más atenuado respecto del observado en la altura que muestra una caída más pronunciada. Las similitudes observadas entre la altura y la potencia de los saltos son de esperar ya que ambos parámetros han sido calculados aplicando fórmulas indirectas. En el caso de la potencia, la fórmula de Sayers y col (1999), al introducir al peso total movilizado como segundo factor, permite una caída menos pronunciada de la potencia que permite compensar relativamente la pérdida de la altura a medida que avanza el test y el peso se incrementa.
Estos resultados son similares a los mencionados por Viitasalo (1985) con estudiantes, saltadores y jugadores de voley que realizaron el test de saltos verticales en diferentes momentos (antes y luego de los entrenamientos y momentos diferentes de la temporada). En todos los casos, la relación entre fuerza y velocidad mostró una curva descendente e incluso reflejó las modificaciones especificidad inducidas por los entrenamientos aplicados en cada caso. No obstante, en los estudios de Viitasalo (1985) la sobrecarga fue aplicada de forma absoluta y no se estableció ninguna relación con el valor de la 1 MR. Del mismo modo, Gorostiaga y col, (2004), aplicaron un test similar con pesos comprendidos entre 10 y 70kg, para valorar las adaptaciones de un grupo de jugadores de fútbol a un programa de entrenamiento de fuerza explosiva. Estos autores indican que este test constituye una metodología válida para reflejar la orientación de las cargas de entrenamiento ya que al cabo de 11 semanas los sujetos manifestaron un incremento significativo sólo en la altura alcanzada al saltar con su propio peso y con 10, 20 y 30 kg. En este caso, tampoco se relacionó el nivel de las cargas aplicadas con los valores de la 1 MR y por lo tanto no es posible establecer con que porcentaje de peso se producen estas mejoras.
Los resultados de nuestro estudio, coinciden con Verkhoshansky, (1996), cuando indica que en los gestos deportivos, al movilizar con la mayor velocidad posible cargas superiores al 40% de la fuerza máxima, la eficiencia del gesto depende progresivamente de la fuerza absoluta, mientras que por debajo de este porcentaje se incrementa la influencia de la velocidad y la técnica de movimiento. Además, si consideramos los resultados de los estudios de Cronin y col, (2003) o Newton y col, (1996), que evaluaron los niveles de fuerza, velocidad y potencia producidas en ejercicios de tren inferior y superior ejecutados con diferentes regimenes de acción muscular, (concéntricos, reactivos y balísticos) e indican que con pesos superiores al 60%, se produce una perdida significativa de la velocidad y un alargamiento de los tiempos de tensión durante la fase concéntrica, es evidente que además de los aspectos técnicos, la variable que más limita la eficiencia del salto es la relación entre el peso corporal y la fuerza máxima. De esta manera, la fuerza máxima constituye una capacidad que limita el rendimiento específico, el cual sólo podrá expresarse adecuadamente cuando el peso corporal o un 90% de este representen sobrecargas inferiores al 40% de la 1 MR.
Al realizar saltos con pesos crecientes las mayores alturas y potencias se logran con las cargas más elevadas (< 40% hasta el 60% de la 1 MR) y a medida que el peso se incrementa (>60%) los niveles de fuerza necesarios para movilizar la carga van siendo significativamente mayores y se necesita más tiempo para lograrlos, de este modo el gesto se hace más lento y se reduce altura y potencia producidas. Por otro lado, con pesos muy altos (>90% de la 1 MR) se pierde la capacidad de saltar o realizar una acción balística. De acuerdo con esto, al hacer ejercicios movilizando pesos con la mayor velocidad posible en un amplio rango de pesos, (~30%-100% de la 1 MR), la interacción entre fuerza, velocidad y potencia permite identificar tres zonas de trabajo bien definidas:
- Zona 1 o de pesos bajos (~30% al 60% de la 1 MR) en donde predomina la velocidad o explosividad.
- Zona 2 o de pesos medios (>60% al 90% de la 1 MR) en donde predomina la fuerza, pero aún se conserva la posibilidad de realizar gestos balísticos
- Zona 3 o de pesos máximos (>90% de la 1 MR) en donde no es posible realizar gestos balísticos y predomina la fuerza máxima.
Además, si consideramos la caída de la potencia producida a lo largo de toda la zona 1 (fuerza explosiva), esta puede dividirse en dos subzonas:
- Pesos bajos (<40%) en donde se alcanzan los valores de potencia más elevados.
- Pesos medios (>40% al 60%), en donde si bien las potencias producidas son muy elevadas ya se determina una perdida superior al 10% que se asocia un alargamiento del tiempo de tensión y convocatoria progresiva de fibras lentas para poder completar el gesto (Hori et al., 2005).
Debido a esto, para evaluar los efectos del entrenamiento de saltabilidad sobre el rendimiento de fuerza explosiva sería suficiente con valorar la relación fuerza-velocidad determinada con los pesos de la zona 1 (30% al 60%) y considerar que una mejora en la zona de pesos bajos (<40%) indica una predominancia de la velocidad o la potencia, mientras que una mejora en la zona de los pesos altos (>40% al 60%) indica un predominio de la fuerza.
Si el test de saltos con pesos evalúa la capacidad de aplicar fuerza en acciones balísticas desarrollas en las zonas 1 y 2, en los ejercicios que implican extender el tren inferior en contra de la gravedad manteniendo una dirección vertical del gesto, debe incluirse cerca del 90% del peso corporal o su totalidad como parte de la masa movilizada (Cormie et al., 2007). Así un sujeto que pese 70 kg y posea una 1 MR de 2.6 por kg de peso corporal, tendrá un valor absoluto de 182 kg (70 kg de su propio peso + 112 externos) siendo su peso corporal el 38% de la 1 MR. De este modo, si el test comienza con el propio peso corporal (38%) y finaliza, como menciona Bosco (1992), con un peso externo similar al de su propio peso corporal (70 kg) el sujeto estará realzando el ultimo salto con un peso total de 140 kg que se corresponde con un 77% del nivel de la 1MR (140/182). Este último peso es extremadamente alto ya que coloca al sujeto dentro de la zona 2 (predominio de la fuerza) dificultando la capacidad de realzar un gesto explosivo-balístico. No obstante, si se desea evaluar la capacidad de realizar gestos balísticos con la mayor eficiencia posible sería más adecuado valorar sólo la zona 1 (fuerza explosiva) que comprende entre el 30% y el 60% de la 1MR. De esta forma, el sujeto anterior debería saltar con ~ 110 kg (70 kg del peso corporal + 40 kg externos), determinando una extensión de la zona 1 entre el 38% y el 60% de la 1 MR. Además, si por efecto de un programa de entrenamiento el sujeto mejora la fuerza máxima hasta 3 kg por kg de peso corporal, podría ampliar su zona de valoración ya que su 1 MR externa sería de 140 kg, su fuerza máxima total, incluyendo el peso corporal aumentaría hasta 210 kg y su peso corporal representaría el 33% de la 1 MR. De este modo, si el test comienza sólo con el peso corporal y finaliza con un peso externo similar al de su propio peso (70 kg), como indica Bosco (1992) el sujeto iniciaría el test con el 33% y lo finalizaría con el 66% de la 1MR.
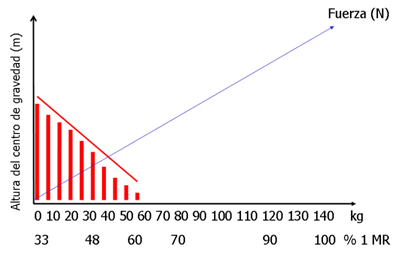
El índice propuesto por Bosco (1992), no debe ser establecido con relación al peso corporal sino con relación a los niveles de fuerza máxima. De esta manera, el índice debería referirse a los limites superiores e inferiores de la zona 1 o de fuerza explosiva, en donde el valor inferior se relaciona con la mayor velocidad de acortamiento muscular y el más alto con una mayor influencia de la fuerza (ver Figura 2), siendo ideal que este 2º punto se situé con un peso próximo al propio peso corporal, ya que de esta manera el propio peso del sujeto representa porcentajes cercanos e incluso menores del 30% de la 1 MR. Así por ejemplo, volviendo al caso anterior, si el sujeto alcanza los 3 kg por kg de peso corporal en el test de 1 MR en sentadilla, cuando salta sin peso externo, actúa incluso menos del 33% de la 1 MR, ya que diversos estudios de segmentación han demostrado que hasta antes del despegue la sobrecarga movilizada equivale es entre el 85% y el 94% del peso corporal (Escamilla et al., 2000, Enoka, 2002) y por lo tanto, en lugar de comenzar con el 33% y finalizar con el 66%, en realidad lo haría entre ~ 30 y el ~60% de la 1 MR (Naclerio, 2006, Naclerio, 2006).
Figura 2. Relación entre altura del salto y peso movilizado en un sujeto que posee 1 MR de 210 kg (incluyendo el peso corporal) en sentadilla con barra libre.
En la Figura 2, los kg constituyen la variable independiente (controlada por el evaluador), mientras que la altura del salto es la variable dependiente que se modifica con relación a los kg movilizados, y expresa el rendimiento en la zona de fuerza explosiva.
Conclusiones
Debido a que la relación fuerza-velocidad establecida en los test de saltos con pesos refleja la capacidad de realizar gestos balísticos, la cual a su vez está limitada por el nivel de fuerza máxima, este test debería ser aplicado para evaluar las modificaciones que se producen en las zonas 1 y 2 (>30% hasta el 90% de la 1MR), determinando la carga en base al nivel de la 1MR incluyendo el peso corporal o el 90% de éste como parte de la resistencia movilizada. Además, la adecuada aplicación de este test debe hacerse considerando el nivel de fuerza máxima o 1 MR medido en un ejercicio similar pudiendo valorar el rendimiento sólo en la zona 1 o de fuerza explosiva que es donde el sujeto manifiesta su máxima capacidad de salto e incluso experimenta perdidas superiores al 10% de la potencia cuando se acerca a los limites determinados por la zona 2 en donde se manifiesta un predominio de la fuerza por sobre la velocidad o la potencia de movimiento.
REFERENCIAS
1. Baker, D (2001). A series of studies on the training of High Intensity Muscle Power in Rugby League Football Player. J. Strength Cond. Res., 15, (2) 198-209
2. Bosco, C (1983). Elasticità muscolare e Forza esplosiva nelle attività fisico-sportive. Società Stampa Sportiva, Roma
3. Bosco, C (1990). Aspetti fisiologici della preparazione fisica del calciatore. Società Stampa Sportiva, Roma
4. Bosco, C., Viitasalo, J. T., Komi, P. V. and Luhtanen, P (1982). Combined effect of elastic energy and myoelectrical potentiation during stretch-shortening cycle exercise. Acta Physiol Scand, 114, (4) 557-565
5. Cormie, P., McBride, J. M. and McCaulley, G. O (2007). The influence of body mas son calculation of power during lower body resistance exercise. J. Strength and Cond. Res, 21, (4) 1042-1049
6. Cormie, P., McBride, J. M. and McCaulley, G. O (2007). The influence of body mas son calculation of power during lower body resistance exercise. J. Strength and Cond. Res, 21, (4) 1042-1049
7. Cronin, J., McNair, P. J. and Marchall, R. N (2003). Lunge performance and its determination. J of sports sciences, 21, 49-57
8. Cronin, J. and Sleivert, G (2005). Challenges in understanding the influence of maximal power training on improving athletic performance. Sports Med., 35, (3) 213-234
9. Dugan, E. L., Doyle, T. L. A., Humphries, B., Hasson, C. J. and Newton, R. U (2004). Determining the optimal load for jump squat: A review of methods and calculations. J. Strength and Cond. Res, 18, (3) 668-674
10. Enoka, R. M (2002). Neuromechanics of Human Movement. Human Kinetics
11. Escamilla, R. F., Lander, J. E. and Garhammer J (2000). Biomechanics of Powerlifting and Weightlifting Exercises, Chapter 39, In Exercise and Sport Science (Eds, Garret, W. E. and Kirkendall D. F) . Lippincott Williams & Willkins., Philadelphia, pp. 585-615
12. Graham, J (2002). Periodizatión Research and Example Application. Strength Cond. J., 24, (6) 52-70
13. Hakkinen, K., Alen, M. and Komi, P. V (1984). Neuromuscular, anaerobic, and aerobic performance characteristics of elite power athletes. Eur J Appl Physiol., 53, 97-105
14. Hori, N., Newton, R. U. and Nosaka, K (2005). Weightlifting Exercise Enhance Athletic Performance That Requires High-Load Speed. Strength Cond. J., 27, (4) 50-55
15. Kellis, E., Arambatzi, F. and Papadopoulos, C (2005). Effects of load reaction force and lower limb kinematics during concentric squat. J. of Sport Sciences, 23, (10) 1045-1055
16. Komi, P. V. and Bosco, C (1978). Utilization of stored elastic energy in leg extensor muscles by men and women. Med and Sci sports and Exc., 10, (4) 261-265
17. Naclerio, A. F (2005). Entrenamiento de fuerza y prescripción del ejercicio, In Entrenamiento personal, bases fundamentos y aplicaciones. (Ed, Jiménez G. A) Inde, pp. 87-133.
18. Naclerio, A. F (2006). Evaluación y planificación del entrenamiento de fuerza en deportes de conjunto. Apunte de catedra. http://www.sobreentrenamiento.com/CurCE/Cursos/Descarga_Material.asp?cur=DC1
19. Naclerio, A. F (2006). Departamento de fisiología (Ed) . Universidad de León, León, pp. 671
20. Naclerio, A. F (2006). Valoración De La Fuerza, Potencia Y Velocidad En Los Ejercicios De Con Resistencias Gravitatorias: Utilización Del Encoder Rotatorio, capitulo 9. In Nuevas dimensiones en el entrenamiento de la fuerza, (Ed, Jimenez, A. c.) INDE (En prensa)
21. Naclerio, A. F (2007). Análisis de la producción de potencia en los ejercicios de fuerza y localización de las zonas de entrenamiento., In Avances en ciencias de la actividad físuica y el deporte. Entrenamiento de fuerza. Escuela de estudios universitarios Real Madrid- UEM 241-276, Madrid.
22. Naclerio, F., Forte, D., Colado, J. C., Benavent, J. Y. and Chulvi, I (2007). Analysis of the Force and Power Produced in the Squat over 52 Weeks Training. Med and Sci sports and Exc., 39, (5) S293
23. Rahmani, A., F., V., Dalleau, G. and Lacour, J.-R (2002). Force/Velocity and power/velocity relationships in squat exercise. Eur J Appl Physiol., 84, (3) 227-232
24. Sale, G. D (1991). Testing Strength and Power, chapter 3, In Physiological Testing of high performance athlete. (Eds, MacDougal, J. C., Wenger, H. A. and Green, H. J.) Human Kinetics, Champaing IL, pp. 21-106.
25. Sayers, S. P., Harackiewicz, D. V., Harman, E. A., Frykman, P. N. and Rosenstein, M. T (1999). Cross-Validation of three jump power equation. Med and Sci sports and Exc., 31, (4) 572-577
26. Verkhoshansky, Y. V (1996). Componenti e Structura Dell impegno explosivo di Forza. Rivista di cultura Sportiva, nº 34, 15-21
27. Viitasalo, J. T (1985). Measurement of force-velocity characteristics for sportsmen in filed conditions. In Biomechanics IX-A, (Eds, Winter, D. A., Normal, R. W., Wells, R. P., Hayes, K. C. and A.E., P.) Human Kinectics., Champin IL., pp. 96-101.
28. Wretmeberg, P., Feng, Y. and Arborelus, U. P (1996). High and Low Bar Squating Techniques During Weight Training. Med and Sci sports and Exc., 28, (2) 218-224
29. Wretmeberg, P., Feng, Y. and Arborelus, U. P (1996). High and Low Bar Squating Techniques During Weight Training. Med and Sci sports and Exc., 28, (2) 218-224
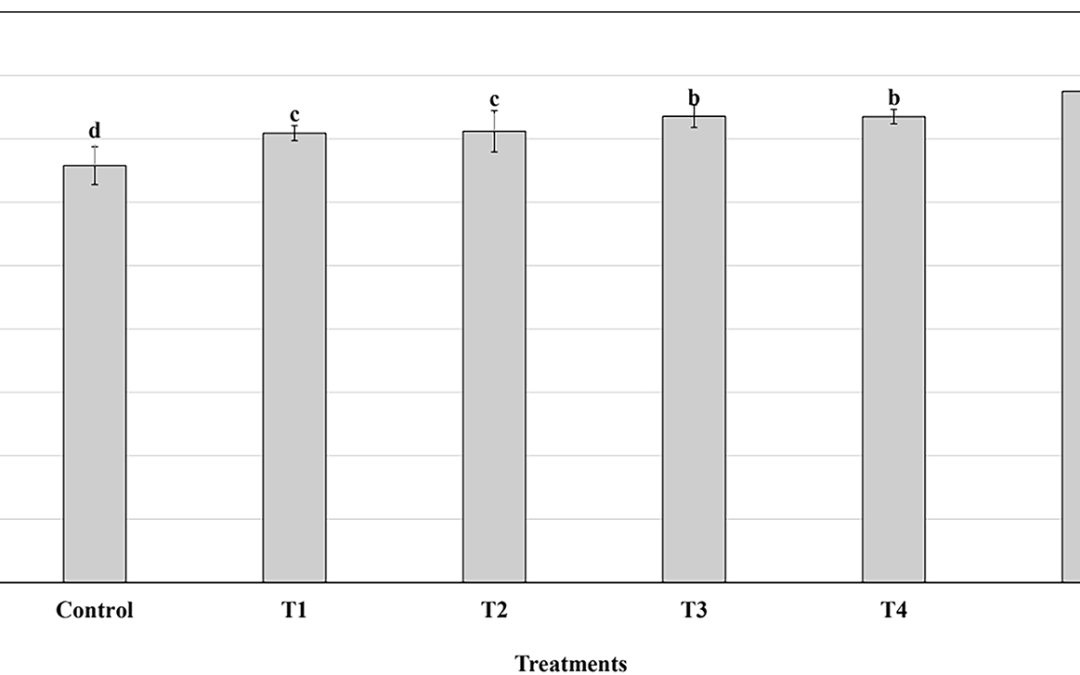
Mejora de las propiedades nutricionales y de textura del jerky reestructurado con polvo de sangre de pato para aplicaciones en kits de comida
Resumen del Estudio sobre el Uso de Polvo de Sangre de Pato en Jerky Reestructurado En un contexto...
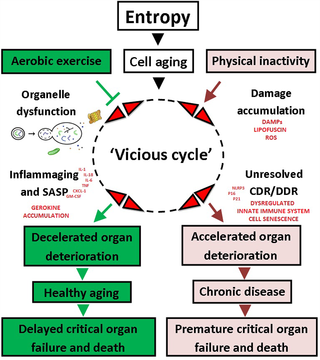
El ejercicio aeróbico a lo largo de la vida protege contra la inflamaging y el cáncer
Ejercicio Aeróbico y su Impacto en el Envejecimiento y el Riesgo de Cáncer La investigación...
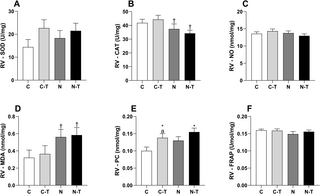
La combinación de nandrolona y entrenamiento de resistencia indujo remodelación cardíaca y estrés oxidativo a pesar de la contractilidad mejorada de los cardiomiocitos
Este artículo investiga cómo la combinación de entrenamiento de resistencia (RT) y el uso de...
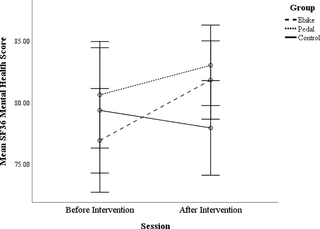
El efecto del ciclismo en la función cognitiva y el bienestar en adultos mayores
El impacto del ciclismo al aire libre en la función cognitiva y bienestar de los adultos mayores...
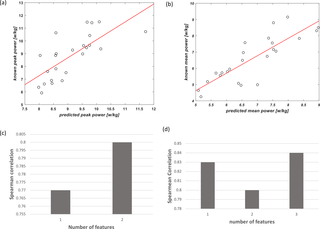
Predicción de las salidas de potencia mecánica anaeróbica del Wingate a partir de una prueba de esfuerzo cardiopulmonar incremental máxima utilizando un enfoque de aprendizaje automático
El Wingate Anaerobic Test (WAnT) se ha establecido como un método efectivo para medir la potencia...