Valoración de la Proporcionalidad Mediante el Método Combinado. Estudio Realizado con 233 Jugadores de Balonmano de Alto Nivel
Raúl P Garrido Chamorro1, Marta González Lorenzo1 y Isabel Expósito1
Servicio de Apoyo al Deportista del Centro de Tecnificación de Alicante.
Artículo publicado en el journal PubliCE, Volumen 0 del año 2004.
Publicado 18 de febrero de 2005
Resumen
Palabras clave: antropometría, phantom, método combinado
INTRODUCCION
La proporcionalidad siempre ha sido la hermana pobre de la antropometría, debido a su poca aplicabilidad al deportista. Esta falta de aplicabilidad se debe a que sus datos se alejan bastante del ideal del deportista. El método del Phantom se ha visto superado por un nuevo enfoque antropométrico basado en la estadística bayesiana, Este modelo se ha denominado Método Combinado y nos permite afinar la proporcionalidad antropométrica. Consiguiendo que esta resulte realmente útil en nuestra valoraciones deportivas. Al comparar a un deportista con una muestra de deportistas que consideramos de referencia, pero este método además nos permite comprar a un deportista con la media se su equipo, o consigo mismo en distintos momentos de su vida deportiva. Representando el impulso definitivo que la proporcionalidad necesitaba para situarse a la misma altura que el somatotipo o la composición corporal antropométricas. En este artículo hemos analizado el método combinado con una muestra de 233 jugadores de balonmano de alto nivel, encontrando que este método es superior al Phantom original.
HISTORIA DE LA PROPORCIONALIDAD
Desde los albores de la humanidad el hombre siempre buscó algo absoluto, alguna ley o principio de simetría, un ideal tal vez que expresase plenamente lo visual de la figura humana. Mucho antes de que nos topemos con la solución propuesta por Poliklitos, debemos de iniciar nuestro viaje histórico en Egipto. En el antiguo Egipto encontramos las primeras referencias a la proporcionalidad, entre cada parte del cuerpo y su todo, este pueblo usaba como valor de referencia la longitud de los dedos.
Los griegos utilizaban, al igual que los egipcios y quizás influenciados por ellos, la proporción para valorar los distintos cánones de belleza. Este pueblo definió los cánones ideales de belleza en función de las proporciones corporales. Por ejemplo si leemos a Polikletos, nos enseña como el cuerpo humano proporcionado tenia una longitud de siete cabezas, mientras que su compratiota, Praxiteles, en sus tratados aumenta esta relación a ocho cabezas (como observamos hemos pasado de usar la longitud del dedo a la longitud de la cabeza).
En el Renacimiento nos encontramos con Leonardo da Vinci. Autor altamente cualificado en casi la totalidad de las ciencias del renacimiento. Este autor nos describe en sus escritos las reglas de proporcionalidad del cuerpo humano en movimiento. El dibujo que representa esta figura ha sido usado frecuentemente para simbolizar la alianza entre le deporte y la ciencia. Leonardo da Vinci retoma las ideas del arquitecto romano Vitruvio (año 15 A.C.).
A caballo entre los siglos XV y XVI nos encontramos, la reluciente figura de Alberto Durero (1471-1528) este autor en su obra, filosofó sobre la proporcionalidad corporal. Sus ideas las podemos encontrar en sus cuatro libros sobre las proporciones humanas. Avanzando en el tiempo nos encontramos con la figura de Gerard Thibault. Este autor en su obra, analiza las dimensiones ideales de un esgrimista, con una riqueza de detalles difícil de ser encontrada incluso en estudios más modernos.
Por tanto podemos afirmar que de una forma genérica, en la antropología física, la altura de la cabeza fue el índice más utilizado para la determinación de la proporcionalidad. Por ejemplo la estatura, según la antropología física consistía en siete u ocho alturas de cabeza, y a partir de esta medida y usando un canon, eran deducidas el resto de las medidas.
Como hemos visto desde el inicio de la proporcionalidad, ésta ha estado muy relacionada con el arte. Ya que los cánones estéticos eran usados tanto en pintura como en escultura. Así en términos artísticos, la obra de Panostsky recopila las normas de la proporción humana. Realizando un estudio pionero e innovador que a la larga, sentará las bases científicas sobre las cuales se iniciará la investigación de los principios, que nos informaran sobre la composición del cuerpo humano.
Los Juegos Olímpicos de Ámsterdam, en 1928, marcan el inicio de la investigación antropométrica en atletas de alto nivel. Este trabajo fue continuado en casi todas las Olimpiadas posteriores, facilitando el nacimiento de los conceptos de proporcionalidad para cada una de las modalidades deportivas.
En el estudio de la proporcionalidad actual el parámetro que se usa para la determinación del canon ideal es la altura. Por tanto hemos evolucionado de la longitud del dedo de los egipcios y de las cabezas de los griegos, hasta llegar a la altura del cuerpo ideal, que se usa en el Phantom actual.
PROPORCIONALIDAD COMO CONCEPTO ANTROPOMETRICO
El concepto de proporción es complementario al clásico concepto de la forma, pero intrínsecamente aporta cualidades que le confieren un carácter diferenciador. La forma se refiere a la estructura global en su conjunto, globalmente, al análisis que se realiza por diversos métodos, que incluyen el somatotipo y el análisis de componentes corporales. En el análisis de la forma, que se realiza mediante el somatotipo, hemos de tener en cuenta que el tercer componente (ectomórfico) está claramente relacionado con la forma del sujeto o grupo que estamos estudiando.
En este artículo nos vamos a ocupar del estudio de las proporciones corporales, es decir nos ocuparemos de la relación que se establece entre las proporciones corporales, y de la relación que se establece entre las distintas partes del cuerpo humano.
La proporcionalidad humana es un concepto de sumo interés para el conocimiento biológico del ser humano, Para este fin es primordial la realización de estudios sobre deportistas, debido a que del análisis de sus proporciones, depende en gran parte su capacidad deportiva y por tanto su rendimiento deportivo. Por tanto, la proporcionalidad corporal es una faceta de gran importancia en el conocimiento de la constitución del ser humano.
Pero por desgracia este parámetro no engloba es sí mismo el concepto de proporcionalidad en su totalidad. Actualmente, los distintos autores, aún no han podido construir un prototipo de proporcionalidad que contenga todas las características necesarias para completar el estudio de la proporción humana.
Debido a que el mayor inconveniente y a la vez la mayor virtud del ser humano es la inmensa variabilidad interpersonal, que se haya intrínsecamente fusionada a las características definitorias de la raza humana. Esta variabilidad se encuentra asociada tanto al sexo como a los estados de crecimiento o a las diferencias raciales. A consecuencia de estas diferencias, la comparación utilizando las medidas directas, puede ser insuficiente para nuestro estudio, debido a que en muchas ocasiones esta medidas dependen, finalmente de la talla del sujeto objeto de nuestro estudio, debiendo utilizar otros métodos para estudiar la proporcionalidad.
Clásicamente, la proporcionalidad se ha estudiado usando el análisis de los índices corporales. Estos índices se han venido utilizando en otras ciencias como la Antropología desde el siglo pasado. El problema de estos índices, (que llevo inevitablemente al desarrollo del Phantom) fue la inexactitud de la mayoría de estos parámetros. Por lo cual, paulatinamente van desapareciendo de los estudios antropométricos actuales.
Debemos tener en cuenta, como veremos más adelante, que este método (Phantom) puede presentar varias dificultades, sobre todo cuando se intentan analizar los resultados, que se obtienen al aplicar su metodología. Debido al difícil análisis de los datos obtenidos, otros autores han propuesto sistemas diferentes: Tanner, recomienda el análisis de la covarianza y un análisis de regresión similar a los estudios sobre relaciones alométricas.
Esta técnica, la alometría, también ha sido recomendada por Hiernaux y May. La alometría, quizás sea el método adecuado para valorar la variación conjunta de dos variables antropométricas.
Otro método de análisis de las proporciones corporales fué desarrollado por Behnke y Wilmore. Para desarrollar el contenido teórico de su método de proporcionalidad, se han basado en las diferencias de los perímetros de un sujeto o grupo, respecto al grupo de referencia. Esta técnica fue denominada somatograma.
METODO DE PHANTOM
La proporcionalidad del Phantom de Ross es una referencia humana originada hace casi treinta años, no existiendo otro modelo más reciente tanto utilizado dentro de la proporcionalidad antropometría. Es un dispositivo de cálculo con valores medios y desviaciones estándar definidas, con más de cien datos entre alturas, longitudes, diámetros, perímetros, pliegues cutáneos y masas y que según Ross su validez reside en la capacidad para cuantificar las diferencias de proporcionalidad en las características antropométrica entre dos grupos poblacionales o entre un grupo poblacional y un individuo.
Ciertas características físicas están ligadas a la performance deportiva dada la gran asociación que existe entre un aspecto somático determinado y el desempeño motor, siendo fundamental el conocimiento de aquellas para su posterior análisis.
Algunas disciplinas atléticas exigen una morfología especial que puede distar mucho de otras pero dentro de ellas se encuentran semejanzas entre sujetos de primer nivel de cualquier país.
La posibilidad que brindan aquellos métodos de mediciones corporales que tratan este tema es muy importante para ser tenidos en cuenta en las diferentes etapas de la construcción de deportistas, llámense iniciación, desarrollo y perfeccionamiento.
La proporcionalidad, como uno de los pilares de la antropometría es la relación de las partes del cuerpo humano, ya sea del propio sujeto o con respecto a los sujetos de un grupo determinado.
Los modelos conceptuales y teóricos se fueron sucediendo a lo largo de la historia, entre los cuales se pueden mencionar el dispositivo de León Battista Alberti (1404-1472), el hombre y la mujer de referencia de Benhke (1974) y la estratagema del Phantom de Ross y Wilson (1974), que posteriormente fue revisado por Ross y Ward (1982). Estos fueron creados con una finalidad particular y ofrecen datos numéricos con los cuales se puede comparar a cualquier ser humano, así es que es Phantom, gracias a su amplia base de datos, representa una referencia teórica humana unisexuada no etaria y no ética utilizada como dispositivo de cálculo para la valoración del crecimiento proporcional.
En este punto los autores se encontraron ante la necesidad de crear un instrumento de medida, que nos permitiera realizar un estudio de la proporcionalidad más fácil de realizar e interpretar.
Por ello, Ross y Wilson propusieron una referencia unisexual y bilateralmente simétrica, estableciendo sus medidas a partir de estudios antropométricos realizados en grandes poblaciones por Garret y Kennedy, Wilmore y Behnke, y Clanser y colaboradores.
Lo cual simplifica el modelo teórico al que nos debemos comparar. El problema de esta simplificación se deriva de la pérdida de la variabilidad intrínseca al ser humano. No sólo en cuanto al sexo (el modelo es asexuado), sino que desprecia totalmente valores como la edad o la raza.
Ésta es por tanto la gran limitación de la teoría del Phantom. Hemos de resaltar el matiz de que el Phantom es asexuado. Siendo éste uno de los pocos valores antropométricos que se pondera independientemente del sexo. Despreciando las cualidades propias del sexo y que tan importantes resultan a la hora de la práctica deportiva.
Este método fue denominado por ellos mismos, como el sistema del Phantom, que podríamos traducir como “ente imaginario”. (Esta traducción aunque correcta me parece poco útil. Por lo que en todo el artículo seguiremos usando el concepto de Phantom).
El nombre de esta teoría se deriva del método usado para calcular la proporcionalidad. Lo que los autores proponen es una comparación de los resultados obtenidos para cada sujeto o grupo, con respecto a los valores de un modelo teórico o Phantom, que se toma como referencia. Por tanto, este método nos permitirá realizar comparaciones de los individuos o grupos analizados, según sus diferencias proporcionales con respecto a este Phantom.
Aunque este sistema fue diseñado en un principio para estudios de crecimiento, posteriormente se ha aplicado en adultos, a diversas poblaciones deportivas y personas con anomalías cromosómicas. Encontrando incluso tendencias de proporcionalidad especificas para determinadas modalidades deportivas.
Este hecho nos lleva a la gran utilidad práctica de este método. Debido a que cuando realizamos una valoración antropometría de una joven promesa, podemos ver cual es su relación con el Phantom de su especialidad. Este dato nos permitirá ir puliendo a nuestro pupilo en función de las características que consigan mejores resultados en su deporte.
GENERALIDADES DEL PHANTOM
En 1974, Ross y Wilson propusieron un nuevo método para el análisis de las proporciones corporales. Al revisar el trabajo original, encontramos como los propios autores nos describen el propósito por el que crearon dicho modelo.
Este propósito no es otro, que utilizar las diferencias en la proporción de un individuo, para compararlo con otros individuos, o grupos de ellos. El fundamento teórico de este método consiste en un modelo teórico o conceptual (Phantom).
Este modelo se obtiene a partir de un amplio número de datos referentes a varones y mujeres, siendo por tanto válido para ambos sexos y cualquier edad. Este método por tanto necesita un referente para realizar las comparaciones entre los individuos y grupos.
Este modelo asexuado es el Phantom. El Phantom, como ya hemos explicado en los párrafos anteriores, fue concebido en sus inicios, como un sistema para evaluar los cambios de proporción que se producen durante el crecimiento. Por tanto, lo que se pretendía era detectar las anomalías en el crecimiento de un individuo o grupo de individuos.
Por ejemplo: detectar el aumento del la talla de un individuo con respecto al ideal. O la disminución del tamaño de las extremidades, etc. Pero debido a la validez del sistema, a lo largo de los años y siendo apoyado en multitud de estudios científicos, los distintos autores han ido ampliando este modelo. Este modelo se ha desarrollado tanto en cuanto a su conceptualización (cuerpo doctrinal), como a su utilización (uso práctico) en distintos grupos humanos. El problema es que su fórmulación aritmética no ha cambiado mucho, pues en la actualidad se mantiene prácticamente igual que en su origen.
El modelo original (creado por Ross y Wilson) del Phantom se elaboró basándose en los siguientes supuestos:
- Es un modelo metafórico y unisexual, lo cual permite la comparación intra e intersexual, eliminando el sesgo debido al dimorfismo sexual. Este punto supone una ventaja al simplificar el modelo teórico de comparación. Pero elimina la importante contribución de variabilidad para la especie humana, que supone la diferenciación sexual. Hay que resaltar que de todo el contenido teórico médico-deportivo, el único parámetro en el que no se dividen a los participantes en función del sexo es este método.
- Todas las variables del Phantom son uninodales, con el valor z=0.0 como moda. Además se distribuyen normalmente.
- La variable que se utiliza como referencia de proporcionalidad es la estatura, aunque podría ser cualquier otra. (Recordemos que para los egipcios era la longitud del dedo y para los griegos la de la cabeza)
- Todas las medidas están reducidas a la misma escala geométrica:
- En el caso de la masa (peso total, o fracciones del peso corporal: muscular, residual, graso u óseo). Esto se consigue elevando a la tercera potencia la relación (170.18/estatura).
- Para la superficie corporal o las secciones de las extremidades, esta relación deberá elevarse al cuadrado.
- Y para las medidas lineales el factor de elevación será la unidad.
- Para el estudio de la composición corporal mediante la estimación de las diferentes fracciones corporales (pesos musculares, etc…) se toma como valor teórico del modelo, un 18.78% de grasa corporal. (Útil para la población general, pero excesivo para la población deportiva. En este subgrupo quizás el valor del porcentaje graso debería estar próximo al 10-12%)
Siguiendo los supuestos que acabamos de describir, se consigue un método de estudio de la proporcionalidad corporal, que evita el problema de las varianzas mezcladas y difíciles de estimar, que presenta el análisis de los índices o medidas relativas.
Ésta es la razón por la cual este método de proporcionalidad ha desbancado completamente a los índices que se utilizaron al inicio de la proporcionalidad antropométrica (IMC por ejemplo).
Además según el razonamiento de Ross, con este método también se eliminan los inconvenientes, que presenta el método de la alometría. Debido a que en el método alométrico, cuanto se acaba el crecimiento de la variable independiente, el valor del coeficiente b (perteneciente a la ecuación alométrica y=axb) tiende a infinito. Este dato invalida la posibilidad de análisis paramétricos, entre diferentes individuos o grupos de la comparación.
Este modelo ha tenido desde su creación una gran aceptación. Debido sobre todo a la aplicación del Phantom a deportistas olímpicos, trabajo que publicó Ross y cols. Por su parte, Chovanova y Pataki estudiaron la proporcionalidad de los lanzadores checoeslovacos también mediante este método.
A pesar de la generalización de este método de análisis de la proporcionalidad, en la literatura médica encontramos también algunos autores que han rechazado esta teoría. Algunos autores rechazan esta teoría porque piensan que no tiene significación biológica relevante.
Otros autores defienden que introduce una mayor covariación entre tejido adiposo y maduración esquelética durante el crecimiento. El mismo autor (Ross), sin embargo nos deja con la duda de si la variación a la que hace mención en su teoría, es debida:
- A la utilización del modelo adulto que representa el Phantom.
- A la utilización de coeficientes de alometría inadecuados.
- A que en realidad las proporciones corporales y la composición corporal cambian con la edad.
Shephard y cols, en sus trabajos sobre proporcionalidad, nos indican que se utiliza una estandarización univariante, para un proceso el crecimiento, que es multivariante y que el uso de puntuaciones Z implica una normalidad de variables que no tiene porque existir.
DESCRIPCION DEL METODO DEL PHANTOM
Como ya se ha indicado, el Phantom consiste en la transformación de las variables originales en puntuaciones Z (uninodales, como la moda en Z= 0.0 y distribuidas normalmente) según la fórmula:
Z=1/s*(V(170.18/E)d-p)
Donde:
Z: El valor de la variable transformaba en el Phantom.
S: Desviación estándar que propone el modelo para la variable estudiada.
V: Valor obtenido de la variable estudiada.
E: Valor obtenido para la estatura .
170.18: Constante de proporcionalidad para la estatura en el modelo Phantom.
d: Exponente dimensional, que permite la linealización de las variables.
- d=1 para las longitudes, diámetros, perímetros y pliegues de grasa.
- d=2 en las superficies corporales o en las áreas transversales.
- d=3 en el peso y otros volúmenes corporales.
Por tanto:
- Valores positivos de Z indican una proporción mayor para la variable estudiada.
- Valores negativos una proporción menor, siempre respecto a la estatura, que es la variable de referencia.
- Valor de cero significa que el valor es igual a ideal del Phantom.
En realidad, estas variables son similares a las que se realizan en estadística, para obtener las puntuaciones típicas de una variable que se supone distribuida normalmente, puesto que en esos casos la puntuación típica de z se define como:
z=(x-µ)/σ
Donde
X: El valor de la variable.
U: La media poblacional de la variable.
O: La desviación estándar poblacional de la variable.
Por tanto, en el Phantom, las especificaciones para las variables son equivalente a las medidas poblacionales de las mismas, igual que sus desviaciones estándar lo son a su homologa poblacional.
V (170.18/E)d
Donde:
V: Valor obtenido de la variable estudiada.
E: Valor obtenido para la estatura.
170.18: Constante de proporcionalidad para la estatura en el modelo Phantom.
d: Exponente dimensional, que permite la linealización de las variables.
- d=1 para las longitudes, diámetros, perímetros y pliegues de grasa.
- d=2 en las superficies corporales o en las áreas transversales.
- d=3 en el peso y otros volúmenes corporales.
Es el término el que sustituye a la x (la variable) en el cálculo de las puntuaciones típicas Z, consiguiendo de esta forma los dos objetivos perseguidos:
- Comparar todas las variables con respecto a la misma estatura, es decir, la de referencia, independiente de la edad o el sexo de los sujetos estudiados.
- Ajustarlas a la misma escala geométrica, mediante el valor de la exponencial d (este valor puede ser 1, 2 ó 3 en función de la variable a estudio).
Una vez desarrollado el sistema aritmético de cálculo de los valores Z, nos queda pendiente describir cuales son los valores que el Phantom atribuye a las diferentes variables, así como a sus desviaciones típicas. Se han obtenido de las descritas por Ross y Marfell-Jones, considerándose las más importantes las siguientes:
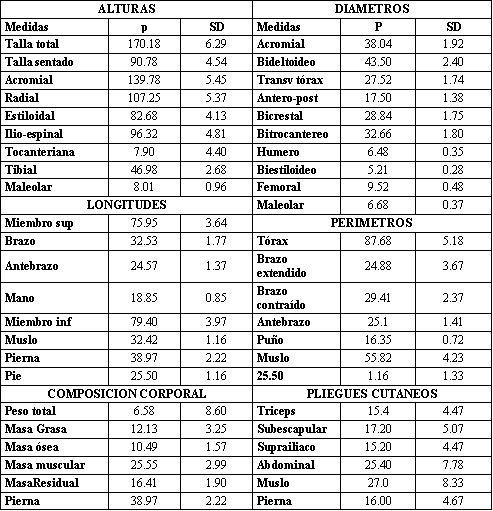
Tabla 1. Valores (P) i desviaciones tipicas (sd) del “Phantom” (Ross, Wd,
& Wilson,n)
La muestra que utilizaron Ross y Wison no la recolectaron ellos mismos, sino que se basaron para obtener los valores de referencia en los datos recolectados por dos líneas de investigación: las de Behnke y Wilmore por un lado y las de Garrett y Kennedy por otro.
Los resultados obtenidos mediante el análisis de la proporcionalidad por el método Phanton suelen representarse gráficamente, tal y como se observa en la figura tomada del articulo de la Dra Kerr publicado en el Asia Pacific J Clin Nutr (1995) 4: 25-29 y con el título: “The elite athlete - assessing body shape, size, proportion and composition”.
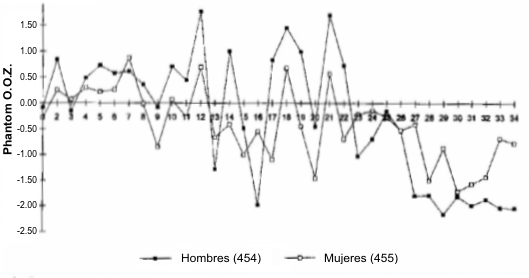
Figura 1.
En este gráfico observamos como varían las características de la muestra en función del sexo. Cada punto significa un valor del Phantom con respecto a las variables antropométricas analizadas. Por tanto, esta proporcionalidad no sólo nos puede servir para analizar los valores de un deportista.
Puesto que además, podemos comparar los resultados obtenidos con los de otro grupo (hombres-mujeres) como en el gráfico anterior, nadadores de un club frente a nadadores olímpicos, etc... Estos valores nos permiten la comparación con uno mismo a lo largo del tiempo, y de un deportista con respecto a un grupo o de dos grupos entre sí.
METODO COMBINADO
El método combinado descrito por el Dr Lentini intenta ofrecernos una
variante del modelo de proporcionalidad antropométrica descrito por Ross.
Mediante el método combinado. El Dr Lentini pretende obtener valores ideales
para poblaciones específicas como la deportiva. (A cualquier nivel) al
compararla con la élite de su deporte, con sus compañeros de equipo o con el
mismo en distintos momentos de una temporada o a lo largo de varias temporadas.
Estos valores nos permiten conocer la distancia estadística entre un sujeto y la
media que nos interesa tipificar. Llamada tipificación Z combinada. Mediante el
Método Combinado intentamos obtener una aproximación de las características de
los deportistas de élite, estos valores no deben servir de guía a los demás
deportivas tanto senior como en las categorías inferiores.
Para calcular la proporcionalidad mediante el método combinado se deben utilizar tres muestras que necesitamos para las los cálculos que describiremos mas adelante. Estas muestras son:
- Los valores de la media u desviación estándar del Phantom de Ross, por provenir de grandes grupos poblacionales de diferentes edades y razas.
- Los valores de las medias y desviaciones estándar de las variables corporales de la muestra que seleccionemos para nuestro estudio, por ofrecer la especificidad y las características de perfil deseado. (en nuestro 233 jugadores e balonmano de ambos sexos)
- El análisis mediante el método Bayesiano de los datos de ambas muestras comparado con un valor individual, Ya que el método bayesiano nos permite combinar diferentes fuentes de información en un solo modelo estadístico.
El método Bayesiano del que hablaremos mas ampliamente mas adelante se diferencia de la estadística clásica o frecuentista en que los datos que se combinan se dividen es dos tipos “a priori” o previa a la realización de un experimento y “actual” que surge de la implementación del experimento mismo. Ambas fuentes de información se combina en una sola distribución de probabilidad llamada “a posteriori”, que se utiliza para efectuar inferencia estadística.
Al analizar deportistas aislado de cualquier disciplina, para que sus datos antropométricos puedan ser valoradas como ideales o de referencia, deberían provenir de competiciones mundiales olimpiadas, de centros nacionales e alto rendimiento o de instituciones y federaciones de primer nivel, debiendo realizar un proyecto similar al MOGAP para este subcampo antropométrico.
Asumiendo que el rendimiento humano es un fenómeno multivariable y que la influencia que tiene el entrenamiento físico y la estructura corporal esta limitada por la variabilidad genética, encontramos la cineantropometría y por supuesto la proporcionalidad antropométrica bien en su modelo clásico de Ross o en su método Combinado de Lentini un punto de acercamiento válido hacia la búsqueda de lo que llaman Hawes y Sovak el “prototipo morfológico”.
METODO BAYESIANO
Vamos a exponer brevemente las características básicas de este método Bayesiano para entender las bases matemáticas del método combinado.
Comenzaremos matizando que la inferencia Bayesiana, en la opinión de Aycaquer, es un enfoque alternativo para el análisis estadístico de datos, que en parte, se contrapone a los métodos que proceden de la estadística clásica o frecuentista.
Si bien las bases de la inferencia bayesiana se originan hace más de dos siglos, su uso cayó prácticamente en el olvido, pasando como una teoría estadística marginal, pero en fechas recientes comienza a asistirse a un uso creciente de este enfoque en el ámbito de la investigación biomédica.
Autores como Mendoza nos explican que la estadística se desprende de alguna forma de las matemáticas, de tal manera que esta rama de la estadística debiera operar según las reglas de la lógica matemática. En esta área del conocimiento se establecen principios generales ( o Teorias), de los cuales se deducen como consecuencia todos los resultados posibles. Si observamos este concepto detenidamente, comprobamos como la estadística clásica no opera de la misma manera, ya que la estadística clásica no posee una teoría general que permita entender cómo se generan e integran todos los procedimientos estadísticos.
En contraste a la estadística clásica o frecuentista, el enfoque bayesiano se constituye como una teoría integrada, planteando una serie de principios muy básicos que se denominan axiomas de coherencia y a partir de estos axiomas de coherencia se deducen todos sus procedimientos, con resultados más generales.
La gran ventaje del análisis bayesiano reside en permitirnos incorporar en un único estudio información de diferentes fuentes de información, no solo objetivas sino incluso subjetivas, por este motivo se concibe en un plano muy general las técnicas estadísticas como mecanismo para la actualización del conocimiento particular o general, individual o colectivo sobre el estado del que guarda la naturaleza (en este caso la proporcionalidad deportiva).
Debemos considerar los métodos bayesianos, con una interpretación distinta del concepto clásico de probabilidad, constituyendo una clara alternativa a la estadística tradicional, debido a que esta ultima esta centrada en el contraste de hipótesis, denominada por contraposición a la bayesiana estadística frecuentista. En esencia estos dos modelos se diferencian en que incorporan información externa al estudio para con ella y con los propios datos observados estimando una distribución de probabilidad para la magnitud -efecto- que se está investigando.
Este método se denomina método bayesiano por basarse originalmente en el teorema de Bayes, publicación póstuma del genial Thomas Bayes en 1763, que en esencia nos permite, si conocemos la probabilidad de que ocurra un suceso, modificar su valor cuando disponemos de nueva información. Vamos a describir el teorema descrito por Thomas Bayes.
Teorema de Bayes
Antes de seguir, conviene recordar un poco la terminología y refrescar el teorema de Bayes.
Vamos a llamar:
- P(A) a la probabilidad de que ocurra el suceso A.
- P(A.B) a la probabilidad de que ocurran los sucesos A y B (ambos).
- P(A / B) a la probabilidad de que ocurra A cuando sabemos que ha ocurrido B (se denomina probabilidad condicionada).
La probabilidad de que ocurra A y B es igual a la probabilidad de B multiplicada por la probabilidad de A condicionada a que haya ocurrido B. Pudiendo expresarlo según la siguiente fórmula.
P(A.B) = P(B) x P(A / B) = P(A) x P(B / A)
Por simetría es obvio que se cumple la tercera igualdad.
Si tenemos un conjunto de posibles sucesos Ai (A1 ... An), mutuamente excluyentes (es decir no puede ocurrir dos de ellos a la vez) y que esto sucesos constituyen todas las posibles situaciones (esto lo podemos expresar también en la siguiente fórmula P(A1)+P(A2)+...+P(An)=1, de tal manera que cuando ocurra alguno de los sucesos A tiene probabilidad 1, esto concepto se denomina en la estadística bayesiana suceso seguro).
Esta teoría se expresa gráficamente en la figura siguiente. El cuadrado en este caso representa a todas las situaciones posibles, que en nuestro ejemplo lo dividimos en tres: A1, A2, A3. Por tanto como observamos el suceso B se puede producir en cualquiera de las tres situaciones.
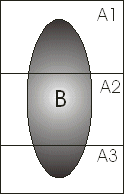
Figura 2.
Si reescribimos ahora la anterior ecuación del párrafo anterior, por ejemplo para A1 tenemos
P(A1.B)=P(A1/B) x P(B) = P(B/A1) x P(A1)
Si aplicamos a esta fórmula un poco de álgebra elemental tenemos:
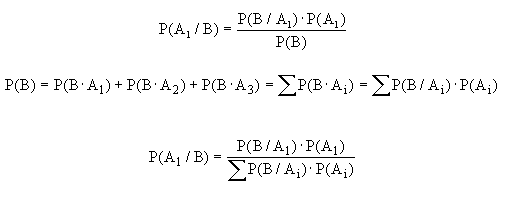
Esta fórmula constituye el famoso teorema de Bayes del cual deriva la estadística bayesiana. Para cualquiera de las otras situaciones (A2,A3) la fórmula es similar.
Ejemplo de aplicación del teorema de Bayes
Pero en nuestro ámbito alejado de las matemáticas, debemos de clarificar esta teoría con unos ejemplos prácticos.
Una de las aplicaciones más intuitiva en medicina este teorema y por ende de la estadistica bayesiana, y con la que todo el mundo está familiarizado, la encontramos en el campo de las pruebas diagnósticas, dicha estadística bayesiana nos permite, conociendo la prevalencia de una enfermedad en la población a la que pertenece un individuo y los valores de sensibilidad y especificidad de la prueba, calcular la probabilidad de que un sujeto que ha dado positivo en el test, verdaderamente tenga esa enfermedad. Es decir la probabilidad de que si obtenemos un diagnostico de rotura fibrilar por ecografía este deportista presente realmente es rotura.
Si llamamos P a la probabilidad a priori de que el sujeto tenga realmente esa rotura, y Q=1-P a su complementaria es decir que el diagnostico se deba a un defecto de la técnica que no permita apreciar dicha rotura en la ecografía, S a la sensibilidad y E a la especificidad de la prueba T; aplicando el teorema de Bayes podemos calcular la probabilidad de que un sujeto presente realmente esa rotura cuando dio positivo ( nos diagnostican de rotura) (valor predictivo positivo de la prueba) y la probabilidad de que no esté enfermo cuando dio negativo(nos diagnostican al deportista de sano) (valor predictivo negativo). Sin más que reescribir la fórmula anterior del teorema de Bayes tenemos:
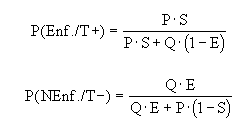
Pongamos algunos números en estas fórmulas: si sabemos que la prevalencia en la población del VIH es de 1/1000 y que el test de VIH que efectuamos tiene una sensibilidad del 98% y una especifidad del 98% ¿Cuál es la probabilidad de que un sujeto que ha resultado positivo sea verdaderamente portador del VIH?
Substituyendo esos valores en la primera de las fórmulas anteriores obtenemos una probabilidad de 0.047, o lo que es lo mismo ¡cerca del 95% de los positivos obtenidos en el test son realmente falsos positivos. Esto inicialmente choca con nuestra intuición, ¿Cómo puede ser que una prueba con una sensibilidad y especificidad altas parezca en la práctica tan mala?. El problema radica en el valor de la prevalencia que es muy bajo y si se refiere a la población general probablemente no será aplicable a un sujeto que acude a consulta a un hospital y al que se le realiza la prueba porque hay otros motivos de sospecha -porque pertenece a un grupo de riesgo, porque presenta síntomas específicos...- y entonces ya no es aplicable la prevalencia de la población general, sino la del subgrupo de población al que pertenece y en el que la prevalencia (probabilidad a priori) de padecer la enfermedad será radicalmente mayor. Sin embargo los cálculos sí que son válidos si estamos pensando en la población general, por ejemplo porque valoramos la posibilidad de plantear un programa de "screening" (detección maxiva de una enfermedad (por ejemplo escoliosis) en una población especifica como la escolar) y habrá que considerar entonces el coste social, personal y económico que supone el tener un gran número de falsos positivos, frente al beneficio de detectar verdaderos enfermos, no vaya ocurrir que sea el propio diagnóstico el que cree una epidemia.
Partiendo de este pequeño repaso al teorema de Bayes, que en esencia es un razonamiento plasmado en una fórmula que nos permite, como en el ejemplo anterior, modificar la probabilidad conocida de que ocurra un suceso cuando tenemos nueva información al respecto. Es decir basándonos en esta nueva valoración estadística nos acercamos mas a la probabilidad real de nuestra muestra.
Metodología bayesiana
Cuando nos referimos a la metodología estadística clásica – conocida como frecuentista- lo que calculamos es la probabilidad de observar un resultado suponiendo que la realidad sea de una manera determinada (a este concepto se conoce como hipótesis nula), sin embargo en la práctica diaria necesitamos los conocimientos para tomar decisiones clínicas, y lo que realmente nos interesa en la practica es conocer la probabilidad de que las cosas sean de una manera determinada una vez conocidos los datos (condicionado a..) que hemos observado. Esta matización es la diferencia que aplicamos en el enfoque bayesiano. Si nos referimos al ejemplo de las pruebas diagnósticas lo que nos interesa en la práctica diaria es conocer el valor predictivo, positivo o negativo, de la prueba no la sensibilidad o especificidad de éstas.
Aunque en la practica estamos habituados a la presentación de los métodos bayesianos con sucesos binarios o dicotómicos (por ejemplo enfermo o sano), esta estadística también es aplicables cuando los resultados son continuos (por ejemplo proporción de pacientes que se lesionan, valor de VO2max o el % graso).
Si utilizamos el análisis estadístico clásico o frecuentista para evaluar por ejemplo la eficacia de un nuevo tipo de entrenamiento frente al entrenamiento anterior, ésta teoría estadística utilizara exclusivamente la información obtenida en el estudio, o experimento. Por el contrario si utilizamos para analizar este tipo de entrenamiento la metodología bayesiana, observamos como es fundamental el concepto de probabilidad a priori (o prior, equivalente Al conocimiento de la prevalencia en las estudios sobre los entrenamientos similares que previamente hemos encontrado en nuestra revisión bibliográfica). El análisis según la estadística bayesiano debe de iniciarse obligatoriamente resumiendo cuantitativamente la información previa existente y externa al estudio, cuyo origen puede ser diverso, desde datos de temporadas anteriores, otros estudios, opinión de expertos o incluso la propias creencias.
Supongamos que se está comparando la mejora aeróbica, cuantificada mediante el VO2 umb. Lo primero que debemos determinar es la distribución de probabilidad de esa magnitud con la información externa de la que se dispone, es lo que se denomina probabilidad a priori y vamos a representar como P (VO2umb). Seguidamente se cuantifica la información que aportan los datos observados en nuestro estudio mediante lo que se denomina función de verosimilitud ( o likelihood), que denotaremos como P(Datos/VO2umb). La verosimilitud representa la probabilidad de los datos observados para cualquier valor del parámetro VO2umb. Podemos ahora utilizar el teorema de Bayes para actualizar el valor a priori P (VO2umb) a la luz de los datos obtenidos y calcular P (VO2umb/Datos), la denominada función de probabilidad a posteriori, es decir cómo de probables son los diferentes valores posibles de VO2umb una vez obtenidos nuestros datos. Según el teorema de Bayes tenemos que
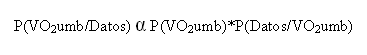
Donde el símbolo indica que el lado de la izquierda es proporcional al lado de la derecha, es decir que son iguales salvo por un término constante (el denominador del teorema de Bayes) que no depende del parámetro de interés VO2umb.
Así pues los resultados se expresan como una función de la probabilidad a posteriori de los diferentes valores de VO2umb. Este proceso se puede representar de forma gráfica, como ahora veremos a continuación.
Supongamos que se está comparando la diferencia entre las medias frecuencia cardiaca máxima de dos grupos de deportistas en un ejercicio anaeróbico intensivo . En la siguiente figura la curva de la parte superior representa la distribución de probabilidad que se espera para la diferencia entre las medias a priori, de acuerdo con la información de la que se dispone. La curva de la parte central representa la función de verosimilitud obtenida a partir de los datos del estudio: probabilidad para cada posible valor de esa diferencia en función de los datos. Por último la curva de la parte inferior corresponde a la distribución de probabilidad a posteriori obtenida al combinar ambas curvas, la correspondiente a la información previa y la obtenida en nuestro estudio.
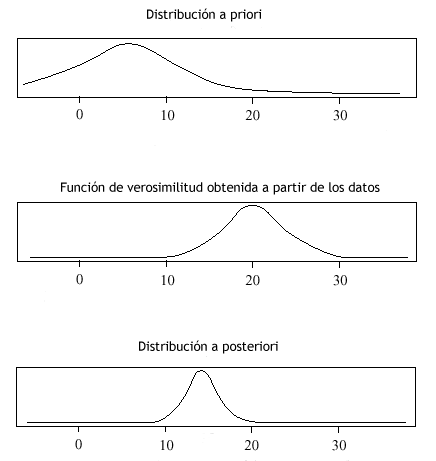
Figura 3.
Ahora las inferencias sobre el parámetro que se estudia -en el ejemplo la frecuencia cardiaca máxima entre los grupos- se basan en utilizar la distribución a posteriori así calculada: podemos obtener a partir de ella, por ejemplo, un valor medio y una dispersión.
Se denomina Intervalo de credibilidad a aquel que garantiza que incluye el verdadero valor de la frecuencia cardiaca con una probabilidad dada, por ejemplo del 95%.
También puede utilizarse la distribución a posteriori para evaluar la probabilidad de que la frecuencia cardiaca máxima tenga un valor igual o mayor que un valor concreto para tomar una decisión.
¿Cómo cuantificar la información a priori?
En la cuantificación de la distribución de probabilidad a priori radica el principal punto de controversia de los métodos bayesianos ya que este punto presenta una, al menos aparente, pérdida de objetividad. Sin embargo está claro que, sobre todo en la toma de decisiones, los juicios sobre la mejora aeróbica, un nuevo tipo de entrenamiento, la posibilidad de aparición de lesiones por este nuevo entrenamiento, etc. nunca se fundamentan únicamente en los resultados de un solo estudio concreto.
Hay que tener presente que el término a priori no implica necesariamente una relación temporal en el sentido de que corresponda a una información obtenida con anterioridad a nuestro estudio, sino que se refiere, en un sentido más amplio, a la información externa a nuestro estudio sea obtenida con anterioridad , simultáneamente o posteriormente a nuestro estudio.
Poseemos diferentes procedimientos para formalizar la distribución de probabilidad a priori y algunos autores han recomendado no limitarse a un sólo método para cuantificarla, sino que debemos utilizar varios de ellos con el fin de evaluar cómo se modifican la conclusiones en cada caso. Es lo que se conoce en términos estadísticos como análisis de sensibilidad.
Desde el punto de vista probabilístico o matemático de la cuestión encontramos tres métodos fundamentales para establecer la distribución de probabilidad a priori:
- Distribución no informativa o de referencia, que corresponde a una ausencia de opinión o de conocimiento clínico a priori y por lo tanto no aporta información a lo que se observa en los datos.
- Distribución a priori escéptica, que considera que la probabilidad de que la hipótesis alternativa sea cierta (existe diferencia entre los grupos) es muy pequeña.
- Distribución a priori entusiasta, que tiene razones fundadas para encontrar diferencias, por lo que determina que la probabilidad de que éstas sean 0 o peor en el grupo de interés tiene una probabilidad muy baja.
El problema radica en que la especificación y cuantificación de la distribución a priori no es una tarea sencilla, especialmente cuando se trata de modelos con más de un parámetro (habituales en al medicina deportiva), como pueden ser los modelos de regresión (fórmulas antropométricas por ejemplo). Por otro lado existe una cierta reticencia por parte de los investigadores médicos a incorporar una distribución a priori con suficiente información, por temor a la posibilidad de que se les acuse de subjetividad.
Campos de aplicación
Aunque la estadística clásica o frecuentista ha supuesto y supone una importante aportación de rigor metodológico en la investigación científica, su utilización encorsetada y dogmática la aleja de su verdadera misión como herramienta y no como ciencia en sí misma.
Cada vez son más las voces que abogan por la renovación y la frescura que aporta el enfoque bayesiano a la estadística cientifica, más cercano a la forma natural de pensamiento y al propio devenir del avance científico. Comenta un epidemiólogo que cuando los médicos comunican de manera informal sus resultados (en charlas, reuniones), el balance entre la biología, la metodología, los datos y el contexto es adecuado en la mayoría de las ocasiones.
Hay un énfasis en la presentación de una "historia" coherente desde el punto de vista epidemiológico o fisiológico. Sin embargo esa sensibilidad se olvida a menudo cuando la información se refleja en las publicaciones, donde la estructura de presentación es mucho más rígida y donde los resultados estadísticos, con su cortejo de P, cobran mucha mayor relevancia. Sin embargo basta efectuar una búsqueda en Medline para comprobar que la utilización de la metodología bayesiana está muy lejos de ser frecuente.
El área de aplicación de la metodología bayesiana es la misma que la de la estadística clásica o frecuentista, pero hay determinadas situaciones en la que su utilización presenta indudables ventajas. Seguidamente vamos a comentar alguna de ellas.
Estudios de equivalencia
Se denomina así a aquellos estudios en los que se trata de verificar la hipótesis nula, es decir que lo que realmente esperamos es que los entrenamientos sean de eficacia similar, aunque uno de ellos presenta otro tipo de ventajas en otras cuestiones que ahora no son el objetivo del análisis, por ejemplo es menos agresivo, o es más barato o tiene menos lesiones, o es de más fácil cumplimiento. Aquí el planteamiento frecuentista resulta un poco retorcido, puesto que la hipótesis nula no se puede probar, sólo se puede rechazar, y ya sabemos que con un tamaño de muestra suficiente siempre podemos rechazar la hipótesis de igualdad. Por lo tanto el enfoque bayesiano resulta mucho más natural.
Monitorización de ensayos clínicos
En los ensayos clínicos que implican observaciones a lo largo de un determinado periodo de tiempo, a medida que éste transcurre se va disponiendo de más información, de tal manera que en algún momento intermedio del estudio la evidencia de los datos puede indicar que un entrenamiento es claramente muy superior al otro, por lo que puede no ser inteligente seguir asignando deportistas a un sistema de entrenamiento inferior.
Y esto es especialmente importante cuando estamos hablando de deportistas de elite que puede ser mucho mayor en el grupo de deportistas que están realizando un entrenamiento claramente peor. O por el contrario, se comprueba que no hay diferencias apreciables entre ambos y quizás no sea razonable seguir gastando esfuerzos y dinero adicional en el estudio. Por ello en el protocolo de muchos ensayos clínicos se indica explícitamente el número y momento en el que se realizarán análisis intermedios de los datos recogidos hasta la fecha, e incluso éstos se efectúan por un Comité de Monitorización independiente.
Pero hay un gran riesgo en parar un ensayo clínico antes de reunir el tamaño de muestra inicialmente previsto para su finalización, ya que el objetivo de cualquier estudio es reunir evidencia para transmitirla a otros con el fin de influir en su práctica diaria, por lo que quizás un enfoque frecuentista de la cuestión, basado únicamente en unas normas para detener el ensayo, justificadas en base a un nivel de significación estadístico, no es suficiente y en cambio es interesante incorporar ese conocimiento previo en el proceso, ya que es el que se pretende modificar y habrá que acumular suficiente evidencia frente a lo que se sabe o se cree saber y no frente a la hipótesis nula.
Meta-análisis
El núcleo central del enfoque bayesiano radica en determinar cómo actualizar cuantitativamente los conocimientos probabilísticos que tenemos de un fenómeno, por lo que parece lógico que en el campo de los meta-análisis, en el que se combina información sobre diferentes estudios, también sea de utilidad ese planteamiento. Dado el auge del meta-análisis dentro de la corriente de medicina basada en la evidencia, es lógico pensar en cada ensayo clínico como un escalón más en la escalera del conocimiento -o de la evidencia- antes que como algo aislado y autocontenido.
Evaluación de datos locales
La posibilidad de efectuar macroestudios no es asequible a cualquier investigador, sin embargo sus propios datos recogidos en un diseño correcto también contienen información valiosa. Con un enfoque frecuentista el obtener un nivel de probabilidad de 0.03 o 0.01 es irrelevante en cuanto a las conclusiones que se transmitan en la discusión de resultados por el investigador, pero si el valor de P que obtiene es 0.07 las cosas cambian radicalmente ya que al no haber obtenido un valor de p inferior a 0.05 el investigador ya no puede poner tranquilamente el marchamo de "se obtuvieron diferencias estadísticamente significativas".
Las conclusiones que ahora exponga van a depender de sus convicciones en cuanto a la validez de la hipótesis del estudio y por lo tanto estará aplicando, sin cuantificar, un enfoque bayesiano de la cuestión. Si es partidario de la hipótesis alternativa dirá que el nivel de P obtenido no llegó a ser estadísticamente significativo pero probablemente se hubiera alcanzado con una muestra mayor. Esto después de haber buscando -sin éxito- algún otro modelo o técnica estadística que le permitiera llegar a la conclusión que va buscando (Todo investigador va buscando algo o es un insensato). Mientras que si es partidario de la hipótesis nula dirá que no hay evidencia muestral suficiente para rechazarla. ¿Es ésta la objetividad de la estadística clásica? Y ¿Hay acaso alguna razón para rechazar ese sentimiento? El que esté libre de culpa que tire la primera piedra.
Parece más que sensato aplicar un enfoque bayesiano en estas situaciones y si, como a menudo suele ocurrir, existen trabajos similares sobre el tema incluirlos en el razonamiento probabilístico y comprobar cómo nuestro estudio modifica o corrobora el conocimiento previo o externo. Por otro lado parece más lógico utilizar un razonamiento continuo, no dicotómico de aceptación y rechazo, ya que no resulta fácil de aceptar la misma hipótesis nula con una P de 0.1 que con un valor de 0.8. La realidad cotidiana nos dice que pocas personas (¿Hay alguna?) toman decisiones de esa manera.
Utilizando el modelo Bayesiano, el investigador conoce únicamente la información brindada por el phantom antes de realizar cualquier medición antropométrica de un grupo de deportistas. A esta información se la puede denominar distribución inicial o como ya se dijo “ a priori”. Una vez efectuada las medidas se cuenta con una nueva fuente de información llamada distribución de la muestra o “actual”. Lo que hace el método combinado es relacionar los dos distribuciones resultando una nueva a la que se conoce como distribución combinada o información “ a posteriori”. La distribución combinada resulta de una ponderación de los dos tipos de informaciones que se están relacionados. Esto quiere decir que si la de la muestra es estas (pocas observaciones medidas), tendrá mayor importancia en su construcción la que brinda el Phantom, pero si la información de la muestra evaluada es representativa (25 o mas observaciones) predomina esta última y el Phantom aporta poco.
MATERIALES Y METODOS
Hemos realizado un estudio observacional y descriptivo a 233 jugadores de balonmano de Alicante que han sido valorados en nuestro centro, durante más de 6 años, entre Enero de 1999 y enero del 2005. Los deportistas masculinos pertenecían a equipos de liga Asobal y los femeninos máxima categoría del balonmano femenino. Los datos han sido recogidos en una base de datos realizada a tal efecto en ACCESS 97, y analizados estadísticamente mediante el programa SPSS 11.01
La muestra estuvo compuesta por 189 hombre el 81% del total y 19 mujeres el 44% del total.

Figura 4.
INSTRUMENTAL UTILIZADO
Una de las razones que favoreció del gran desarrollo de la Cineantropometría fue el bajo costo de los instrumentos necesarios para elaborar las mediciones. El material básico para realizar una antropometría básica es el que vamos a describir a continuación:
Báscula

Figura 5.
Se utiliza para determinar el peso corporal total. En realidad, mide la fuerza con la que el deportista es atraído por la tierra y no la masa corporal propiamente dicha. Sin embargo, está establecido que esta fuerza representa la masa corporal. Es conveniente usar modelos que estén validados y que tengan una precisión de 100 gramos. Y su peso máximo debe de ser de al menos de 150Kgs.
Para su calibración de utilizarán pesas de diferentes kilos abarcando la escala de la muestra que se va a medir (bajo, medio y alto).
Tallímetro

Figura 6.
Utilizado para medir la altura del vértex y la talla sentando.
Consiste en un plano horizontal adaptado, por medio de una guía que acompañan a una escala métrica vertical o un cursor anclado a un carro de medida, que se instala perpendicularmente a un plano base.
La precisión necesaria es de 1mm. Se calibrará periódicamente mediante la comprobación con otra cinta métrica de la distancia entre la horizontal y los diferentes niveles del cursor deslizante.
Paquímetro o Compás de Pequeños Diámetros

Figura 7.
Es un compás de corredera graduado, de profundidad en sus ramas de 50mm, con capacidad de medida de 0 a 259mm.
Sirve para medir los diámetros óseos. Normalmente acompañan al conjunto del antropómetro. La precisión es de 1mm.
Plicómetro o Compás de Pliegues Cutáneos

Figura 8.
También llamado espesímetro o plicómetro.
Mide el espesor del tejido adiposo en determinados puntos de la superficie corporal.
Su característica básica es la presión constante de 10gr/cm2 en cualquier abertura. La precisión debe de ser de 0.1mm. Los márgenes de medida oscilan entre 0 y 48mm.
Un método simple para calibrar este instrumento es fijarlo a un torno y suspender pesos desde la rama inferior.
El compás debe ser ajustado para que las ramas permanezcan abiertas en cualquier posición, manteniendo una presión de 10gr/mm2 para los diferentes pesos de calibración.
Cinta Métrica o Cinta Antropométrica

Figura 9.
Utilizada en la determinación de perímetros y para la localización del punto medio entre dos puntos anatómicos.
Existen diversos tipos en el mercado pero debe de ser flexible pero no elástica, preferiblemente metálica, de anchura inferior a 7mm.
Es importante que disponga de un espacio sin graduar antes del cero y con una escala de fácil lectura que permita una identificación fácil de los números.
La precisión debe de ser de 1mm.
El muelle o sistema de recogida y extensión de la cinta deben mantener una tensión constante y permitir su fácil manejo.
Se recomienda que las unidades de lectura estén en centímetros exclusivamente.
MEDIDAS ANTROPOMETRICAS
Toma mucho tiempo y mucha práctica desarrollar un buen sistema de medición en parámetros antropométricos, especialmente en medición de pliegues cutáneos.
El seguir procedimientos estandarizados incrementa la precisión y por tanto la validez y exactitud de la mediciones. A continuación explicaremos más claramente como hemos realizado las mediciones antropométricas para obtener datos más fiables.
Antes de describir las medias antropométricas vamos a recordar la posición que debe adoptar el estudiado para la mayoría de las mediciones:
Debe permanecer el sujeto de pie, con la cabeza y los ojos dirigidos hacia el infinito, las extremidades superiores relajadas a lo largo del cuerpo con los dedos extendidos, apoyando el peso del cuerpo por igual en ambas piernas, los pies con los talones juntos formando un ángulo de 45º. Esta posición es llamada en Cineantropometría como la “posición de atención antropométrica” o “posición estándar erecta”.
Esta posición es más cómoda para el estudiado, diferenciándose con respecto a la posición anatómica en la orientación e las manos.
Peso
Figura 10.
El peso es la determinación antropométrica más común. Es de gran utilidad para observar la deficiencia ponderal en todos los grupos de edad y el retraso del crecimiento en los niños.
En el sentido estricto, no debería de usarse el término peso corporal sino el de masa corporal, que es el que realmente medimos.
El instrumental necesario para su medición será una balanza validada con una precisión de 100gr. Esta medida se expresa en Kilogramos.
El peso corporal está compuesto de masa magra y masa grasa. A su vez, la masa magra se compone de: masa muscular, vísceras, huesos, sangre, linfa y también comprende los lípidos de las células.
Al peso corporal en condiciones patológicas, pueden sumarse edema (líquido intracelular aumentado), ascitis (líquido en cavidad abdominal), organomegalias (aumento de las vísceras) e incluso parasitosis (carga de helmintos o áscaris).
En adultos se utiliza la medición del peso actual expresado en porcentaje teórico y en peso actual expresado en porcentaje del peso habitual previamente registrado en dicho deportista.
La magnitud del cambio en estos dos datos y su correlación permite estimar la trascendencia del peso actual y precisar el carácter agudo o crónico de la desnutrición u obesidad, con sus diferentes repercusiones.
En la valoración del peso deben excluirse sujetos con tendencia a la retención de agua y edema.
Al tomar el peso, se deben considerar las siguientes precauciones:
- El sujeto se colocará en el centro de la plataforma de báscula, distribuyendo el peso por igual entre ambas piernas, en posición erguida, con los brazos colgando lateralmente, sin que el cuerpo esté encontrado con ningún objeto a su alrededor, y sin moverse.
- El deportista se situará con el mínimo de ropa sin zapatos ni adornos personales y después de haber evacuado la vejiga, además hay que evitar la pesada después de una comida principal.
El cerebro, el hígado, el corazón, los riñones y otros órganos internos forman en conjunto una parte apreciable del peso corporal, pero cambian relativamente poco con una mala nutrición.
Pero el peso en una determinación seriada nos hace perder mucha información muy útil en un deportista, así en un deportista que esté perdiendo peso deberemos saber si es peso es de porcentaje graso o muscular.
Igualmente si el deportista está realizando un periodo de musculación deberemos saber si esa ganancia de peso corresponde a músculo.
Talla o Estatura

Figura 11.
La estatura se define coma la distancia entre el vértex y el plano de sustentación. También se denomina como talla en bipedestación o talla de pie, o simplemente talla.
El instrumental necesario para realizar esta medida es un estadiómetro con una precisión de 1mm.
La medida de esta variable se da en centímetros.
La estatura de un individuo es la suma de cuatro componentes:
- las piernas.
- la pelvis.
- la columna vertebral.
- y el cráneo.
La medición debe realizarse con el sujeto de pie, sin zapatos, completamente estirado, colocando los pies paralelos y con los talones unidos (apoyados en el borde posterior) y las puntas ligeramente separadas (formando aproximadamente un ángulo de 60º), las nalgas hombros y cabeza en contacto con un plano vertical.
La cabeza se mantendrá cómodamente erguida con el borde orbitario inferior en el mismo plano horizontal que el conducto auditivo externo (Plano de Frakfurt).
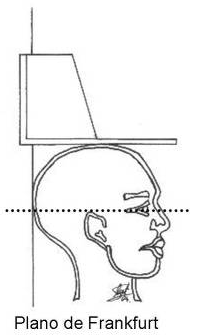
Figura 12.
El antropometrista realiza una tracción a nivel de los procesos mastoideos, para facilitar la extensión completa de la columna vertebral.
Los brazos colgarán a lo largo del cuerpo de una manera natural con las palmas de las manos frente a los muslos.
Se puede pedir al sujeto que realice una inspiración profunda para obtener la extensión máxima de la columna.
Se desciende lentamente la plataforma horizontal del estadiómetro hasta contactar con la cabeza del estudiado, ejerciendo una suave presión para minimizar el efecto del pelo.
Es importante considerar el cabello demasiado espeso en la medición de la talla, aplastando el cabello y haciendo contacto con el vértice de la cabeza.
La escala graduada debe ser de dos metros y permitir una exactitud de 1cm. Los ojos del examinador deben estar por lo menos a la misma altura del sitio donde el panel movible hace contacto con la cabeza.
La estatura para adultos de 60 a 90 años de edad puede ser estimada por medio del largo de la rodilla cuando no se puede medir la estatura de pie.
La estimación de la estatura puede ser utilizada en parámetros de la evaluación del estado de nutrición, incluyendo referencia sobre el peso para la talla, ecuación de gasto energético, ecuación de área de superficie corporal y creatinina para la talla e índices de masa corporal.
El largo de pierna también se puede utilizar junto con otros indicadores antropométricos para preveer el peso en individuos mayores que no pueden ser medidos por métodos convencionales.
Medidas Transversales o Diámetros
Son las medidas lineales realizadas en sentido horizontal y que se caracterizan en general a los diámetros.
Las podríamos definir como la distancia tomada en proyección, entre dos puntos anatómicos medida en cms.
La posición que se mantendrá en el estudio será la que hemos definido previamente como de atención antropométrica. Las excepciones se comentarán en sus correspondientes medidas.
El instrumento para realizar estas medidas en el antropómetro o compás para grandes diámetros y el paquímetro para los pequeños diámetros.
En cuanto a la técnica que debemos usar: la rama de ambos instrumentos se coge entre el dedo pulgar e índice descansando sobre el dorso de la mano. El dedo medio se utiliza para localizar el punto anatómico deseado. Hay que aplicar una presión firme sobre las ramas para minimizar el espesor de los tejidos blandos.
Los datos obtenidos se usan para el cálculo del somatotipo y del porcentaje óseo. Las más utilizadas son las que vamos a describir a continuación.
Principales Diámetros Antropométricos
A. Biepicondíleo del Femur
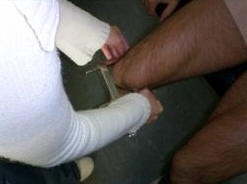
Figura 13.
Distancia ente el cóndilo lateral y medial del fémur. El antropometrista se sitúa delante del estudiado mientras el individuo estará sentando y se hará su medición formando un ángulo de 90º entre la pierna con el muslo, sin que los pies toquen en el suelo. Se mide sólo al lado derecho. Las ramas del calibre pequeño miran hacia abajo en la bisectriz del ángulo recto formado a nivel de la rodilla.
B. Biepicondiliano de Húmero
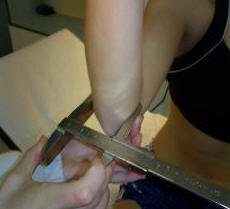
Figura 14.
Distancia entre el epicóndilo y la epitroclea que son el condilo lateral y medial del húmero, respectivamente. El antropometrista se sitúa delante del estudiado.
El brazo se horizontaliza y el antebrazo forma un ángulo de 90º con el brazo para facilitar la medida, con la palma de la mano hacia el mismo y los dedos juntos y extendidos hacia arriba.
El examinador colocará sobre los dos cóndilos del codo y sin ejercer demasiada presión, las dos astas del calibrador tipo vernier, permitiendo reposar el codo en la base de la escala del calibrador, las ramas del paquímetro apuntan siempre hacia arriba en la bisectriz del ángulo recto formado a nivel del codo.
La medida es algo oblícua, por estar la epitroclea en un plano algo inferior al epicóndilo.
Para comprobar que se esta midiendo únicamente la anchura de la estructura ósea del codo, se deberá hacer deslizar el calibrador hacia abajo y si éste lo hace sin ofrecer resistencia, la medición será correcta. Solamente se mide el del lado derecho.
C. Biestiloide
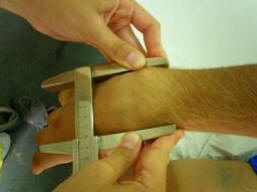
Figura 15.
Distancia entre la apófisis estiloides del radio y del cúbito.
El antropometrista está delante del estudiado que estará sentado con el antebrazo en pronación sobre el muslo y la mano flexionada con la muñeca en un ángulo de 90º.
Las ramas del paquímetro están dirigidas hacia abajo en la bisectriz del ángulo de la muñeca. Se tomará la medida del lado derecho.
Medidas Circunferenciales o Perímetros
Son caracterizadas por las medidas lineales realizadas circunferencialmente. En antropometría se llaman perímetros.
Posición: El estudiado mantendrá la posición de atención antropométrica o estándar erecta, explicada anteriormente. Aunque hay algunas excepciones que se comentarán en sus correspondientes medidas.
Instrumental: Se utiliza la cinta antropométrica flexible e inextensible. La medida se da en cms, con una precisión de 1mm.
Técnica: El antropometrista sujetará la cinta con la mano derecha y el extremo libre con la mano izquierda. Se ayudará con los dedos para mantener la cinta métrica en la posición correcta, conservando el ángulo recto con el eje del hueso o del segmento que se mida.
Se sitúa la cinta sobre la zona al nivel requerido, sin comprimir los tejidos blandos y estando perpendicular al eje longitudinal del segmento que se esté midiendo. La lectura se hace en el lugar en que la cinta se yuxtapone sobre si misma.
A continuación vamos a describir los principales perímetros.
Principales Perímetros
A. Muslo 1 (1cm)
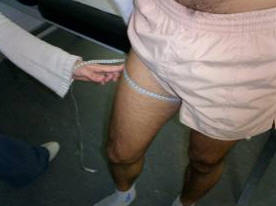
Figura 16.
Es al perímetro del muslo tomado un centímetro por debajo del pliegue glúteo.
El estudiado está de pie, con las piernas ligeramente separadas y el peso distribuido por igual entre ambas piernas.
El antropometrista ha de mantener la cinta perpendicular al eje longitudinal del fémur. Es conveniente para facilitar la medición el situarse al lado derecho.
B. Perímetro de la Pierna
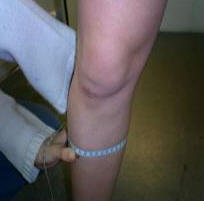
Figura 17.
Perímetro medido a nivel de la máxima circunferencia de la pierna.
Vamos a explicar esta medida con más detalle dada su importancia para los posteriores cálculos antropométricos.
El sujeto estará de pie, recto, con las piernas separadas ligeramente y el peso distribuido de manera uniforme entre ambas piernas.
La referencia anatómica que debemos usar es el valor donde se encuentra el máximo perímetro con respecto a la técnica de medición.
El antropometrista se sitúa a la derecha del sujeto frente a la cara lateral de la pierna, manteniendo la cinta perpendicular al eje de la pierna.
Se registra el valor máximo del perímetro de pierna tras situar la cinta a diferentes niveles.
Este punto será el nivel para la posterior medición del pliegue correspondiente.
Se facilita la medición si se coloca sobre una banqueta.
C. Perímetro del Brazo Contraído o Perímetro de Brazo
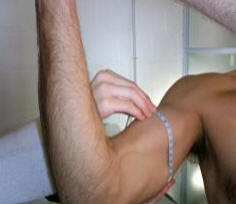
Figura 18.
Es el perímetro máximo del brazo contraído voluntariamente. El estudiado se encuentra en posición erecta, con el brazo en antepulsión y horizontal. El antebrazo se coloca en supinación completa y a en flexión de 45º aproximadamente.
Este mismo punto es el que utilizaremos para la posterior medición de los pliegues del miembro superior.
El perímetro del brazo, expresa la reserva actual de proteína muscular. Su disminución aguda se relaciona con el grado de hipercatabolismo y de gluconeogénesis y junto con el índice de excrección creatinina / talla de 24 horas, lo que permite valorar el estado de la proteína músculo-esquelética.
D. Antebrazo
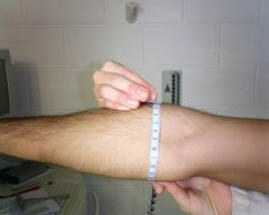
Figura 19.
Es el perímetro máximo del antebrazo.
El estudiado estará con el codo extendido, músculos del antebrazo relajados y mano en supinación.
El antropometrista buscará la máxima circunferencia el antebrazo que normalmente no está a más de siete centímetros por debajo de la cabeza radial.
Los Pliegues Cutáneos
Posición
El estudiado mantendrá la posición de atención antropométrica. Las excepciones se comentarán en sus correspondientes medidas. La musculatura del estudiado tiene que estar relajada.
Técnica
El pliegue cutáneo se toma con los dedos índice y pulgar de la mano izquierda, manteniendo el compás en la mano derecha perpendicularmente al pliegue y abriendo la pinza unos 8cm. Se eleva una doble capa de piel y su tejido adiposo subyacente en la zona señalada, efectuando una pequeña tracción hacia afuera para que se forme bien el pliegue y queden ambos lados paralelos, y se mantiene hasta que termine la medición.
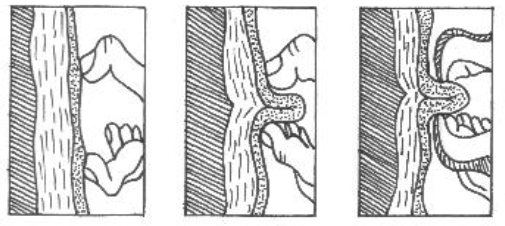
Figura 20.
Con la mano derecha se aplica el compás, colocándolo a 1cm. del lugar donde se toma el pliegue, perpendicular al sentido de este y en su base.
La lectura se efectúa aproximadamente a los dos segundos después de colocar el compás, cuando se desacelera el descenso de la aguja. La cantidad de tejido elevado será suficiente para formar un pliegue de lados paralelos.
Los pliegues cutáneos se medirán en lado derecho, dando el valor medio de tres mediciones, pudiendo descartar las claramente erróneas. Las repeticiones no se harán pliegue a pliegue, sino tras terminar todos los pliegues incluidos en el estudio, evitando así comprimir la zona.
Nunca se atrapará músculo en el pliegue y una buena técnica para comprobarlo, es indicarle al estudiado que realice una contracción de los músculos de la zona cuando se ha cogido el pliegue. Se liberará el pliegue y se volverá a realizar la toma válida con la musculatura relajada.
Pliegues Cutáneos
A mediados de los años 90, se utilizó el grosor de la grasa subcutánea midiendo los pliegues cutáneos, basándose en investigaciones previas, que midiendo el grosor de los pliegues cutáneos en diferentes sitios del cuerpo encontraban una relación moderada a fuerte entre las mediciones de dichos pliegues y la cantidad de grasa corporal.
Desde entonces se utiliza como un indicador de la grasa corporal total en el ámbito clínico, debido a que este sistema es fácil de realizar, y de bajo costo, es ideal para grandes estudios epidemiológicos. Así como, en la evaluación del estado nutricional de nuestros atletas. Además, los pliegues cutáneos se utilizan para estimar la distribución de grasa regional a través de la determinación de la relación de grasa subcutánea del tronco y las extremidades.
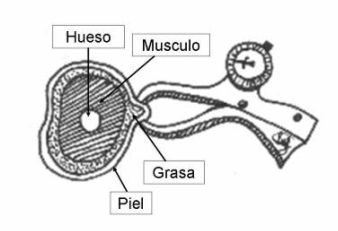
Figura 21.
Cualquiera que sea el lugar elegido, se debe tomar en cuenta que un pliegue está constituido por dos capas de piel y el panículo adiposo, que se encuentra en el tejido subcutáneo.
Se debe pellizcar firmemente un pliegue cutáneo longitudinalmente y levantarlo ligeramente entre el índice y el pulgar de la mano izquierda, teniendo cuidado de no incluir el músculo subyacente. Se aplica el plicómetro aproximadamente a 1cm. por debajo de los dedos del operador y a una profundidad semejante a la del pliegue, mientras que éste se sigue sosteniendo suavemente durante toda la medición.
Un error muy común es sujetar el pliegue exclusivamente con el plicómetro, sin sostener el pliegue con los dedos de la mano.
Se deben dar un promedio de 4 segundos para tomar la lectura. Deben hacerse tres mediciones y calcularse la media de los resultados, si los valores varían entre una y otras mediciones más del 10%, se deberá tomar mediciones adicionales. Una vez tomada la medición se debe retirar suavemente el plicómetro, abriendo sus astas sin dejar de sujetar el pliegue con la mano izquierda, para evitar lastimar al sujeto.
Se debe leer la medición del plicómetro al 0.1mm más cercano. Los lugares más apropiados para la toma del pliegue, varían con la edad, el sexo y la precisión para localizar cada punto.
A continuación vamos a definir los principales pliegues cutáneos:
A. Pliegue Cutáneo Tricipital
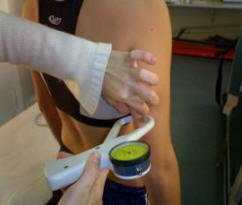
Figura 22.
Es la medición más práctica en todos los grupos de edad, y tanto en la escasez de reservas energéticas así como en la obesidad.
Es un índice aproximado de la magnitud de reserva energética endógena, proveniente de triglicéridos y de sustratos metabólicos.
Este pliegue se medirá eligiendo cuidadosamente el sitio en el que se había utilizado del punto medio del brazo, que no es otro que el punto medio ente el acromion en su punto más superior y externo y la cabeza del radio en su punto lateral y externo.
La medición se practicará con el brazo relajado y colgando lateralmente.
El pliegue formado de manera paralela al eje longitudinal, con el pulgar y el índice de la mano izquierda se separará del músculo subyacente y se medirá en ese punto, colocando el plicómetro perpendicularmente al pliegue.
Técnica de medición: El compás se aplica a 1cm. por debajo del pliegue formado en la línea media de la cara posterior del brazo, a nivel del punto medio marcado entre acromion y cabeza radial.
Para la medición el brazo estará relajado, con la articulación del hombro en ligera rotación externa y el codo extendido.
B. Pliegue Cutáneo Subescapular

Figura 23.
El lugar de medición corresponderá al ángulo interno debajo de la escapula, (punto más inferior del ángulo inferior: se marca a 2cm. en la línea que corre lateral y oblicua siguiendo el clivaje de la piel).
Deberá tener un ángulo de 45º en la misma dirección del borde interno del omóplato (o sea hacia la columna vertebral) Se medirá justo abajo y lateralmente al ángulo externo del hombro.
Para realizar esta medida, se palpa el ángulo inferior de la escápula con el pulgar izquierdo, en este punto hacemos coincidir el dedo índice y desplazamos hacia abajo el dedo pulgar, rotándolo ligeramente en sentido horario, para así tomar el pliegue en la dirección descrita anteriormente.
En sujetos obesos se deberá desprender energéticamente el pliegue del músculo subyacente y esperar varios segundos a que el plicómetro deje de moverse, para que la medición se pueda realizar.
Técnica de medición: El sujeto se sitúa de pie, erecto, con los brazos colgando a lo largo del cuerpo. El compás se aplica a 1cm. de distancia del pliegue formado en la referencia citada.
C. Pliegue Cutáneo Suprailiaco
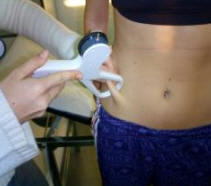
Figura 24.
Se medirá justo inmediatamente por arriba de la cresta ilíaca, en la línea axilar media, en forma oblicua y en dirección anterior y descendente (hacia la zona genital).
Técnica de medición: El compás se aplica 1cm. anterior al pliegue formado en la línea medioaxilar, justo por encima de la cresta ilíaca.
El sujeto puede abducir el brazo derecho o colocarlo sobre el tórax, llevando la mano sobre el hombro izquierdo.
D. Pliegue Cutáneo Abdominal
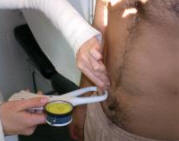
Figura 25.
Situado lateralmente a la derecha, junto a la cicatriz umbilical en su punto medio.
El pliegue es vertical y corre paralelo al eje longitudinal del cuerpo.
Para otros autores está situado lateralmente a 3-5cm de la cicatriz umbilical.
E. Pliegue Cutáneo del Muslo Anterior
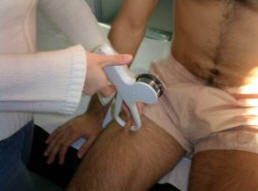
Figura 26.
El pliegue se toma en la parte anterior del muslo, en el punto medio entre la doblez inguinal y el borde proximal de la rótula.
El pliegue es longitudinal y corre a lo largo del eje mayor del fémur. El peso corporal deberá recargarse sobre la pierna que no se esté midiendo.
El plicómetro debe estar colocado en dirección vertical, 1cm. por debajo de los dedos que sostienen el pliegue.
Técnica de medición: El sujeto puede estar sentado o bien tener el pie sobre una banqueta. El compás se aplica a 1cm. de distancia del pliegue formado en él punto de máximo perímetro, en el lado medial de la pierna derecha, con la rodilla flexionada 90º. La pierna debe estar relajada. Si el antropometrista tiene dificultades en la toma de este pliegue, el estudiado puede sostener con ambas manos su muslo en esta posición o contar con la ayuda de otro antropometrista que atrapará con sus dos manos el pliegue.
F. Pliegue Cutaneo de Pantorrilla o Pierna Medial
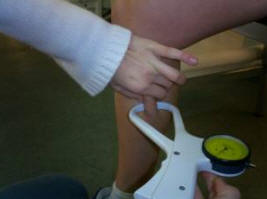
Figura 27.
El pliegue se deberá desprender a la altura de la máxima circunferencia de pierna en la parte interna de la misma, en dirección vertical y corre paralelo al eje longitudinal de la pierna.
El sujeto estará con la pierna en ángulo recto y el pie colocado sobre un banco.
Además de estas mediciones vamos a valorar la composición corporal de nuestros deportistas, Calculando el % Graso según la fórmula de Faulner, la masa muscular según la fórmula de Martin, la masa ósea según la fórmula de Rocha y la masa residual según la fórmula de Wuch. Todas ellas reflejadas en la siguiente tabla.

Tabla 2. Fórmulas utilizadas para el cálculo de los componentes
corporales
CALCULO DEL METODO COMBINADO
Vamos a exponer la sistemática utilizada para el cálculo del método combinado de Lentini.
1) En primer lugar se calcula la Media (mM) y la desviación estándar (deM) de una variable corporal de los sujetos (n) de la muestra evaluada para tomarla como ideal o de referencia:
Por ejemplo en la atura de nuestra muestra:
mM: 174.80
deM: 12.54
n: 873
2) Se buscan para esa variable los valores de la media del Phantom (mP) y la desviacón estándar del Phanton (deP).
Por ejemplo para la talla
mP: 170.18
deP: 6.29
3) Se calcula la media combinada (mC) para la variable analizada, utilizando la media del Phantom (mP) y la media muestral (mM).
mC= (mP+n*mM)/(n+1)
En nuestro ejemplo:
mC= (170.18+873*174.80)/874=175.20
4) Se calcula la desviación estándar del método combinado (deC), utilizando el del Phatom (deP) y e de la muestra (deM):
deC= (((n-1)*deM2+deP)/(n+1))0.5
En nuestro ejemplo:
deC= ((872*12.542+6.29)/874) 0.5= 12.48
5) Se realiza una tipificación Z combinada (TZC) con la mC, el deC y el valor de la variable para un individuo (wm), según el método combinado:
TZC- (wm-mC)/deC
En nuestro ejemplo:
TZC= (185.2-175.80)/12.48=0.75
RESULTADOS
En la siguiente tabla vamos a mostrar los valores de la media y la desviación estándar de nuestro estudio, para el subgrupo asexuado, para los varones y para las mujeres
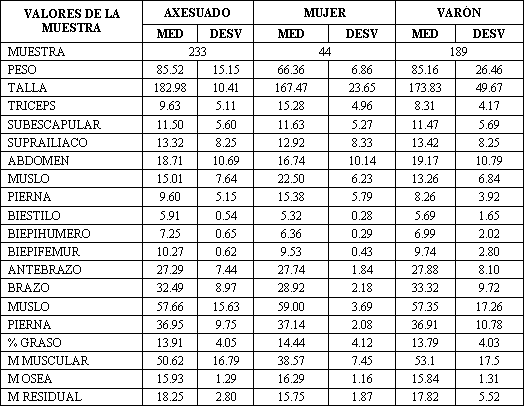
Tabla 3.
En la tabla 4 mostramos los valores para el modelo asexuado (independiente del sexo) tanto del Phantom como de la muestra de 233 jugadores de balonmano analizados.
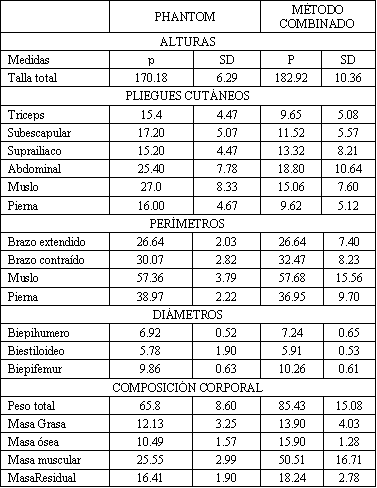
Tabla 4.
Esta misma relación la aplicamos para los 189 varones que componían nuestra muestra comparando los valores del Phantom de Ross y del método combinado de Lentini en la tabla 5.
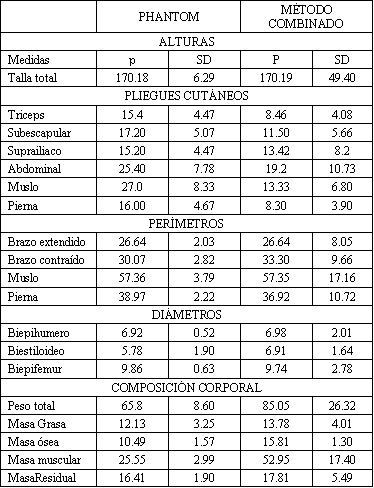
Tabla 5.
En la tabla 6 se muestran los valores de referencia para el calculo de la proporcionalidad utilizando el Phantom de Ross y el método combinado de Lentini para las 44 jugadoras de balonmano de nuestra muestra.
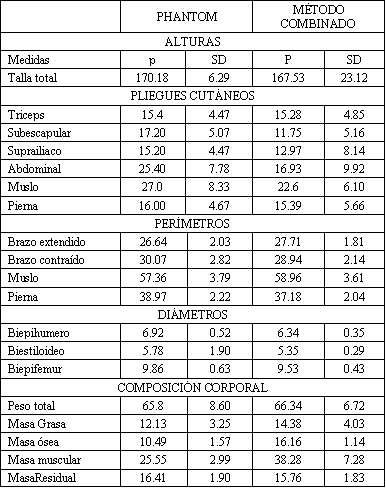
Tabla 6.
En el siguiente grafico mostramos los valores de la proporcionalidad utilizando los valores del modelo del Phantom de Ross. Observamos como los valores oscilan entre -4 y + 4 unidades. Esto significa que nuestro deportista esta muy lejos de su ideal. Pero estos datos no se deben al alejamiento del deportista de su ideal sino a alejamiento del Phantom de Ross del ideal real para este jugador.
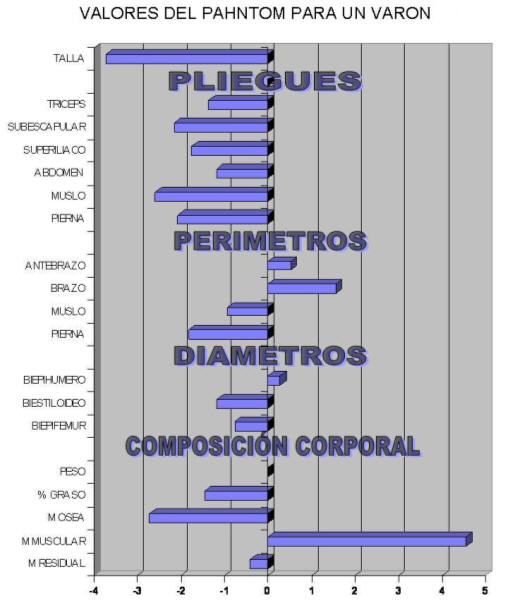
Figura 28.
Si afinamos una poco mas nuestra proporcionalidad, vamos a utilizar el método combinado de Lentini, pero ya que en el original Phantom de Ross no se hace diferencias en función del sexo vamos a tipificar los valores en función del modelo asexuado. Observando que los valores oscilan entre -0.8 y +0.4. Es decir afinamos nuestros valores llegando a detectar más fácilmente las desviaciones con respecto a la media.
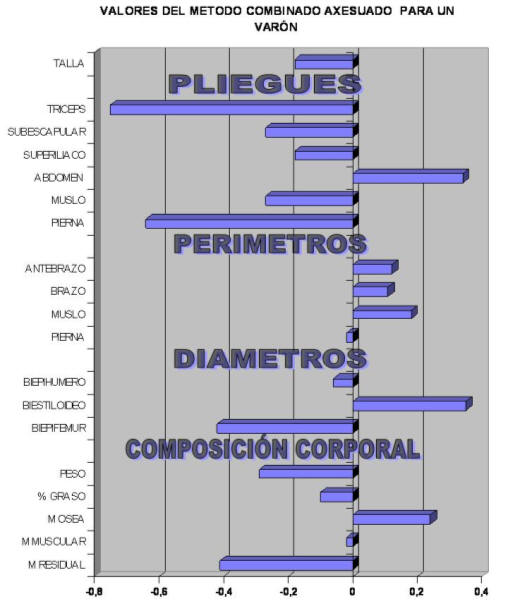
Figura 29.
Pero lógicamente cuanto más afinamos en la muestra más fiable es la proporcionalidad calculada. Así si usamos los valores para los jugadores masculinos. Los valores obtenidos son mas útiles que en el modelo axesuado. Observemos como los valores oscilan en esta ocasión entre -0.7 y +0.3, es decir más próximo del cero ideal.
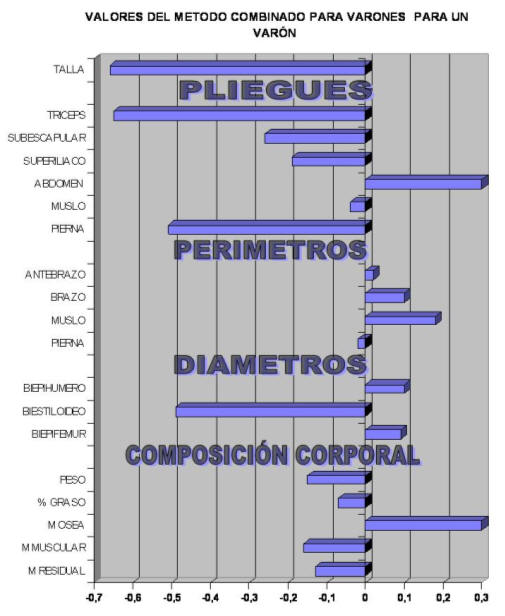
Figura 30.
Para concluir la tipificación de la proporcionalidad en los varones vamos a comparar los tres gráficos anteriores. Observando como el jugador ejemplo se adapta más al método combinado de Lentini que al Phanton original de Ross. Así mismo observamos como los valores son mas útiles cuánto más afinamos en la población de referencia.
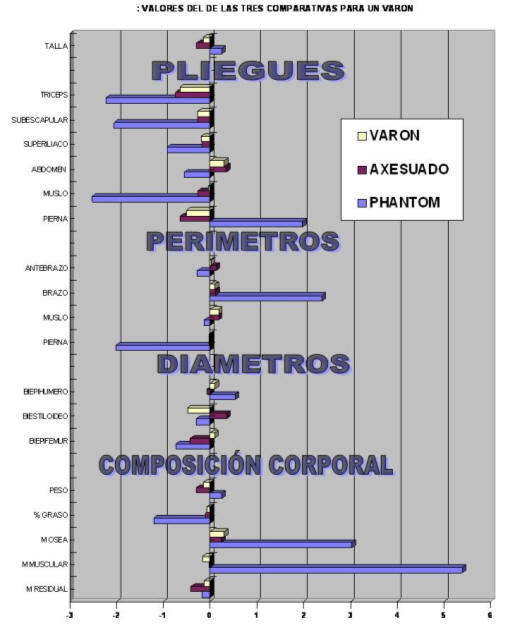
Figura 31.
En la siguiente tabla mostramos los valores numéricos de la tipificación por los tres modelos. Observando como el que mas refleja la situación individual del deportista es la tipificación con los jugadores masculinos.
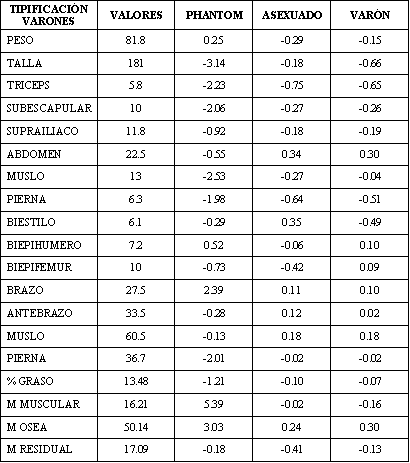
Tabla 7.
En el siguiente grafico al igual que hemos hechos anteriormente vamos a tipificar una deportista femenina con los valores del Phantom de Ross. Observamos como este modelo se acerca mucho del ideal de las jugadoras y por tanto los valores oscilan entre -3 y +6. Siendo este modelo poco adecuado para afinar los valores de la proporcionalidad en la mujeres jugadores de balonmano.
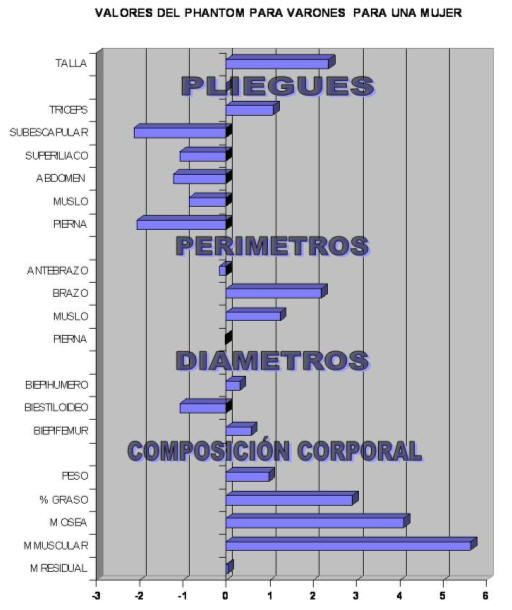
Figura32.
Manteniendo la tradición marcado por el Phantom de Ross, vamos a utilizar el modelo combinado de Lentini con los valores del modelo asexuado hallado en nuestro estudio. Al ser las mujeres solo el 19% de nuestra muestra, los valores aunque más cercanos que los del Pahnton original, se alejan todavía demasiado del ideal de la jugadora femenina. Oscilando los valores entre -2.6 y +1.
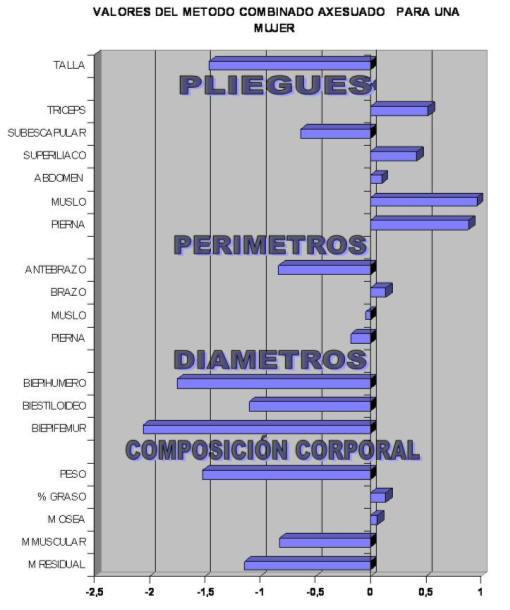
Figura 33.
Si realizamos la tipificación del modelo combinado de Lentini según los valores obtenidos en nuestra muestra para las mujeres, obtenemos que todos los valores oscilan entre -2 y +0.5. Este grafico refuerza la idea de que cuanto más próxima es la muestra que usamos a nuestro deportista de referencia, más útil es el modelo combinado para la tipificación de la proporcionalidad del deportista
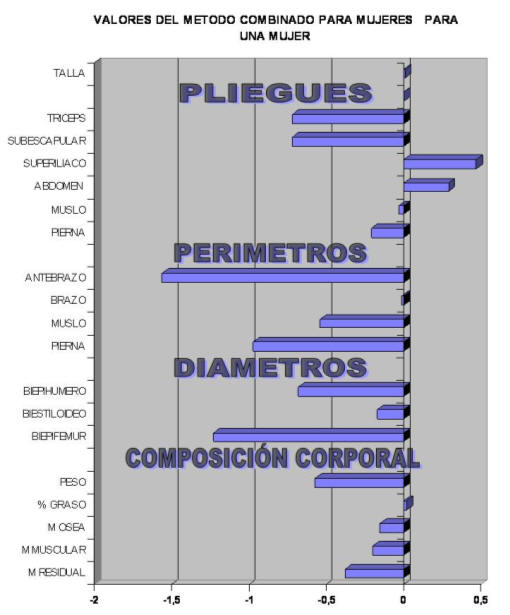
Figura 34.
Al comparar los tres gráficos anteriores observamos como el método combinado es muy superior a la hora de determinas la proporcionalidad que el método de Phantom. Si nos fijamos en las dos gráficas del modelo combinado de Lentini, Observamos que si la población es del mismo sexo que el deportista de referencia, los valores de la tipificación se acercan más al 0.
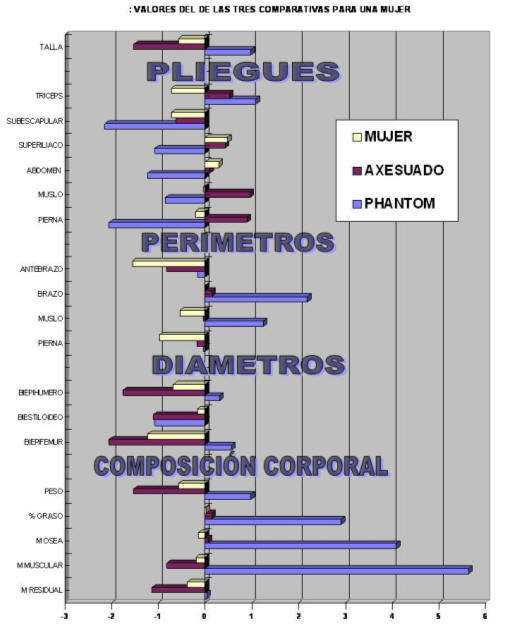
Figura 35.
En la siguiente tabla mostramos los valores para la tipificación para los tres modelos, Observando como la mas próxima al 0 es la del modelo combinado de Lentini tipificado según los valores de la jugadora. Siendo este modelo superior al asexuado debido a la poca importancia que en la asexuada tiene el sexo femenino.
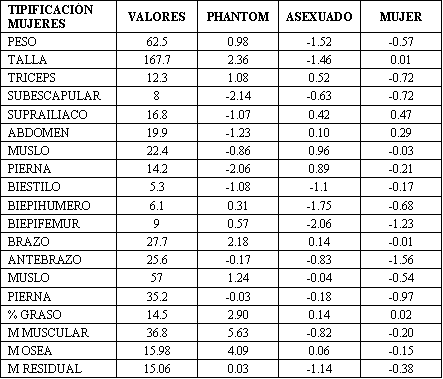
Tabla 8.
DISCUSION
Si admitimos que un deportista tiene un valor de proporcionalidad adecuado cuando su tipificación se acerca a 0 (es decir más próximo esta al ideal), observamos como en todas las comparativas analizadas en nuestro articulo el modelo combinado de Lentini supera claramente al modelo del Phanton de Ross.
Este modelo debe se usarse buscando la población más adecuada para nuestra comparación. Lo ideal seria compararlo con los deportistas olímpicos de cada especialidad. Necesitando unos valores para el modelo combinado similares a los del Mogap para el resto de la antropometría(20).
Otra utilidad es la tipificación con los valores de un equipo. Esto significaría por ejemplo que podríamos hallar la tipificación de un jugador con respecto a los de su equipo. Esto nos permitirá saber las variables que diferencian la antropometría de un deportista con respecto a los de su equipo, permitiéndonos afinar las características antropométricas de este sujeto.
Otro de los posibles campos de actuación de este método de proporcionalidad es la compasión de un deportista consigo mismo a lo largo de su trayectoria deportiva. Esto nos permitirá determinar la evolución antropométrica de un deportista conforme avanza su tecnificación.
CONCLUSION
A modo de conclusión sobre el método combinado, se puede detallas los siguientes puntos:
- Es recomendable utilizar el método combinado en deportistas de alto rendimiento debido a que no realiza el ajuste por una altura y se mantienen el orden de las variables originales.
- La tipificación Z combinada, base del método combinado, refleja fielmente la información contenida en la muestra. Además de su sencillez práctica, sus resultados permiten facilitas la interpretación de los datos analizados, y dado que estos debe de acercarse a 0, lo hace visualmente muy atractivo.
- Una característica importante del método combinado es su fácil implementación y la posibilidad que brinda al investigador, gracias al modelo estadístico Bayesiano, de combinar fuentes independientes de información tales como la de la muestra y la del Phantom
- Ya que las muestras para combinar con la base del Phanton son especificas, se pueden tener valores ideales de cada disciplina deportiva y de cada país.
El método de proporcionalidad combinado nos parece más útil que el la proporcionalidad del Phantom. Ya que permite comparar a cada deportista con los que practican su mismo deporte.
Referencias
1. Carter JEL (1984). Introduction: The Kinanthropometric Approach. In: Carter JEL, ed. Physical Structure of Olympic Athletes Part 11: Kinanthropometry of Olympic Athletes, New York: Basel-Karger: 1-6
2. De Onis M, Onyango AW, Van den Broeck J, Chumlea WC, Martorell R (2004). Measurement and standardization protocols for anthropometry used in the construction of a new international growth reference. Food Nutr Bull.Mar;25(1):S27-36
3. Esparza f (1993). No Disponible. cineantropometria.ed: femede
4. Faulkner JA (1968). Physiology of swimming and diving. Falls H, editores. Exercise physiology. Baltimore: Academic Press
5. Freedman Laurence (1996). Bayesian statistical methods. BMJ; 313: 569-570
6. Lilford R J and Braunholtz D (1996). For Debate: The statistical basis of public policy: a paradigm shift is overdue. BMJ; 313: 603-607
7. Lohman T.G., A.F. Roche, R. Martorell (2004). No Disponible. anthropometric standardization referenceual
8. Martin, A. D (1990). Anthropometric estimation of muscle mass in men. Medicine and Science in Sport and Exercise 22, (5), pp. 729-733
9. Molinero L. M (2002). El método bayesiano en la investigación médica. Asociación de la Sociedad Española de Hipertensión - www.seh-lelha.org/bayes1.htm
10. Redmond Carol K., Theodore Colton (2001). Bayesian methods Biostatistics. Bayesian methods Biostatistics
11. Riener R, Frey M, Proll T, Regenfelder F, Burgkart R (2004). Phantom-based multimodal interactions for medical education and training. the Munich Knee Joint Simulator. IEEE Trans Inf Technol Biomed
12. Ross WD, Wilson NC (1974). A stratagem for proportional growth assessment. Children in Exercise. In: Hebbelinck M, Borms J, eds. ACTA Paediatrica Belgica
13. Ross WD, De Rose EH, Ward R (1988). Anthropometry applied to sports medicine. Dirix A, Knuttgen HG, Tittel K, eds. The Olympic book of sports medicine. London: Blackwell: 23-265
14. Silva L.C., Benavides A (2001). El enfoque bayesiano: otra manera de inferir. Gaceta Sanitaria. Domingo 1 Julio. Volumen 15 - Número 04 p. 341 346
15. Spiegelhalter David J, Myles Jonathan P, Jones David R, and Abrams Keith R (1999). Methods in health service research: An introduction to bayesian methods in health technology assessment. BMJ; 319: 508-512