HSS Dept., University of Dayton.
Resumen
INTRODUCCION
Hay poca duda acerca de la relación positiva entre la fuerza muscular (S) y la masa corporal (M). Sin embargo, continúa la discusión acerca de cual es la mejor manera de expresar la fuerza en función de la masa corporal con el propósito específico de comparar valores individuales o grupales. Esto tiene su origen en el respaldo teórico y empírico que ha recibido la relación directa de S con M2/3 en lugar de con M. La expresión de la fuerza ajustada por M sería S.M-2/3 y puede ser utilizada para realizar comparaciones tanto grupales como individuales. Las bases teóricas se centran en el principio de “similitud geométrica”, el cual sugiere que S, un factor bidimensional, y M, un factor tridimensional, conforman la siguiente relación: S.M2/3 (1). De esta manera, S podría expresarse como S.M-2/3 para ajustar el efecto de M. El respaldo empírico de la validez de la expresión S.M-2/3 aplicada a mediciones de la fuerza isométrica (fuerza de prensión) o a mediciones de fuerza con resistencia variable para diferentes poblaciones puede hallarse en diferentes estudios (2-6).
La estatura, o la talla (H), también pueden utilizarse para ajustar los valores de la fuerza máxima. Debido a que es un índice de longitud, un factor unidimensional, entonces H2 debería ser proporcional a S. Sin embargo, no hay disponible evidencia empírica como para comprobar esto para la fuerza. Además, no existe respaldo teórico para explicar de qué forma H y M podrían ser utilizados de manera multivariada para ajustar valores de S, debido principalmente a su colinearidad. Finalmente la masa corporal es claramente la variable de ajuste de la fuerza más ampliamente utilizada. De hecho, no se puede hallar evidencia de un ajuste por H para cualquier medición de la fuerza, y consecuentemente, H no será considerada en los presentes datos.
Existe evidencia para refutar la afirmación de que el exponente óptimo de M para el ajuste de los valores de la fuerza es 2/3. Batterham y George (7) hallaron que el exponente universal de 2/3 para M no elimina el sesgo entre levantadores olímpicos de pesas de nivel elite, un hallazgo replicado con levantadores de potencia (5). Sin embargo, en este último estudio, Vanderburgh y Dooman afirmaron que la razón por la cual la aproximación con el exponente de 2/3 tiende a producir un “sesgo” en las categorías de mayor peso se debe a que la mayoría de los competidores se encuentran en las categorías de peso mediano (lo cual no es sorprendente, ya que M tiende a estar normalmente distribuida en la población). Debido a que estos levantadores tienen más competencia, uno no debería sorprenderse al observar que los levantadores en las categorías de peso mediano tienden a tener los mayores valores de S.M-2/3. Además, cuando Batterham y George (7) eliminaron a los levantadores más pesados (aquellos que no tienen límite de peso) de sus análisis, el exponente resultante para M fue 0.68, casi idéntico a 2/3. Otros han reportado que los intervalos de confianza al 95% para los exponentes de M, para levantadores de elite (8) niños de edad escolar (9) y mujeres adultas (10), no contienen al valor de 2/3. Las explicaciones que se ofrecen para esto son la dificultad para dar cuenta la excesiva influencia de la grasa corporal, el nivel de entrenamiento y el estadio puberal (6, 7). Cuando se consideran estos factores de confusión, la evidencia que respalda la utilización de la convención S.M-2/3 parece confirmarse en cierta medida.
Para comparar a dos individuos de diferente tamaño con algún índice de S, uno podría dividir el peso levantado por cada uno (S) por M2/3 y comparar los valores resultantes. Los valores mayores corresponderán al individuo con mayor S ajustada por M. De manera similar, este índice puede ser calculado para una muestra entera de sujetos y de esta manera pueden aplicarse test a estos valores para evaluar diferencias grupales. En general este proceso es casi análogo al análisis de covarianza (con M como la covariable) con la diferencia de que se utiliza la más simple de las pruebas t. Una limitación de esta aproximación es que el exponente 2/3 de M no es estadísticamente tan apropiado como el exponente específico real de la muestra, el cual maximiza el control del efecto independiente de la masa corporal. Por lo tanto puede argumentarse que las comparaciones individuales de la fuerza pueden llevarse a cabo convenientemente y apropiadamente utilizando el exponente 2/3 de M, mientras que las comparaciones grupales, las cuales requieren algún tipo de análisis estadístico inferencial, pueden hacerse de una mejor manera calculando el exponente específico de la muestra.
Sin embargo, la convención de expresar S en términos de M como S.M-2/3 no ha sido ampliamente aceptada por los fisiólogos del ejercicio o por los expertos de la aptitud física como una forma factible de calcular la fuerza ajustada por M. Las razones probablemente son muchas y variadas pero probablemente incluyen, la conversión problemática del índice, cuyas unidades son kglevantados.kg-2/3. Los expertos de la aptitud física y los fisiólogos del ejercicio están probablemente familiarizados con la utilización del índice S/M y los valores asociados, los cuales se consideran “por encima del promedio” o “pobres”. Por ejemplo, un levantamiento en press de banca mayor al peso corporal, o S/M>1, se considera frecuentemente como excepcional para una mujer. Por lo tanto, una mujer con un S=70 kg y con un M=70 kg tendría una puntuación de 1.0 kglevantado.kg-1. Sin embargo utilizando la convención S.M-2/3, la misma mujer tendía una puntuación de 70.70-2/3, o 4.12 kglevantados.kg-2/3. Las unidades de este último índice son diferentes y, por lo tanto, el mismo no puede ser comparado con índices estándar. Además el valor de 4.12 kglevantados.kg-2/3 debe ser evaluado contra una nueva “conversión”, lo cual sugiere que las puntuaciones excepcionales para el press de baca ahora están por encima de 4.12. El segundo problema con el índice S.M-2/3 es que es difícil, sino imposible, realizar cálculos a mano, algo que el personal de evaluación de la aptitud física e incluso los individuos comunes pueden hallar problemático, particularmente en el campo de la evaluación.
Un índice simple utilizado y desarrollado por la Federación Internacional de Levantamiento de Potencia (IPF), el índice Wilks, se utiliza actualmente en las competencias de la IPF para determinar quién es el “Campeón de Campeones”, o quién es el levantador que realizó el mayor levantamiento teniendo en cuenta las diferencias en la masa corporal. El índice es simplemente un número adimencional que se saca de una tabla publicada (11), la cual se calcula en base al peso corporal del competidor, con una apreciación de 1/10 kg, multiplicado por el total de peso levantado. El valor resultante ajustado es el que se compara entre los levantadores para determinar quién es el “Campeón de Campeones”. Este índice ha sido recientemente validado para ser utilizado con hombres y mujeres levantadores de potencia de nivel elite (6), teniendo en cuenta el levantamiento total (press de banca + peso muerto + media sentadilla) o teniendo en cuenta solamente el levantamiento en press de banca.
Para hacer comparaciones de S ajustadas por M entre individuos que no son de nivel elite, uno podría simplemente aplicar el índice Wilks. Sin embargo, esto puede ser problemático por varias razones. Primero, este índice está basado en datos reales de levantadores de potencia de nivel elite (press de banca, peso muerto y media sentadilla), y no en datos de sujetos que no son de nivel elite utilizando otras mediciones de la fuerza. En otras palabras, su utilización es válida solo para comparaciones específicas con sujetos de elite. Segundo, el índice se basa en una transformación polinómica de datos reales obtenidos con levantadores de potencia de nivel elite. Dicha transformación fuerza a que la curva se ajuste a los datos, y esto puede tender a perjudicar a los levantadores pertenecientes a las categorías de peso mediano (aquellos de los cuales uno esperaría un rendimiento superior, ya que la mayoría de los competidores se encuentran en estas categorías de peso-como se discutió previamente). Esta transformación permite que la curva (la función que “nivela el campo de juego”) se “doble en ambos extremos” por lo cual el “Campeón de Campeones” no siempre es un levantador perteneciente a las categorías de peso mediano. Como se mencionó previamente, este “falso” efecto ha sido observado y contrastado por otros investigadores (5, 6).
Otro problema relacionado con la naturaleza polinómica del índice de Wilks es que no tiene base teórica, ya que dicha transformación fuerza a que la curva de mejor ajuste se adecue a datos reales, a diferencia del modelo alométrico el cual cuenta con un mayor respaldo (e.g., S.M-2/3). En otros artículos (5-7) puede ser encontrada más discusión acerca del tema del ajuste del modelo versus a la adecuación teórica. Dado que el modelo alométrico tiene respaldo tanto empírico como teórico para una variedad de sujetos con una variedad de mediciones de la fuerza, el argumento contra la utilización del índice de Wilks para sujetos que no son de nivel elite parece apropiado.
En conclusión, el cálculo del índice S.M-2/3 es defendible tanto teórica como empíricamente para mediciones de la fuerza entre sujetos que no son de nivel elite, sin embargo es algo engorroso para aplicarlo en situaciones prácticas. El índice Wilks tiene una utilidad mucho más práctica, pero muestra características cuestionables de generalización para sujetos que no son de nivel elite y además tiene pocas bases teóricas. Por lo tanto, parece aparente la necesidad de desarrollar un índice simple del tipo Wilks, basado en la aproximación alométrica. El propósito de este artículo, es por lo tanto, calcular y presentar dicho índice I, en forma de una tabla, en base a M, la cual es multiplicada por S para producir un nuevo S ajustado, o Sadj. La Sadj tendría las mismas unidades de S, podría ser fácilmente calculada a mano, y está basada en una transformación matemática del índice alométrico S.M-2/3. De esta manera, podría considerarse como una expresión apropiada de S ajustada por M.
METODOS
Debido a que el objetivo fue desarrollar un índice simple similar en utilidad al índice de Wilks, se tiene que asumir y elegir un punto de referencia. Primero, se asumió que el ajuste apropiado de S por M debería ser S.M-2/3. Como se mencionó previamente, este punto ha recibido considerable respaldo tanto teórico como empírico, particularmente para expresiones de la fuerza para hombres y mujeres. Segundo, se seleccionaron los pesos de referencia de 73.0 kg para hombres y 60.0 para mujeres como aquellos que tendrían un índice de “1.00”. Esta selección, aunque completamente arbitraria, sirve como punto de referencia a partir del cual se pueden calcular todos los otros índices. Podría elegirse cualquier combinación de pesos y la convención resultante debería ser matemáticamente equivalente a cualquier otra elección. De hecho, lo mismo es cierto para un índice para hombres y mujeres. Sin embargo, la elección de valores de referencia específicos del sexo, permite que se produzca una desviación mínima con respecto al puntaje real para valores cercanos a los valores medios estimados de masa corporal, para hombres y mujeres. Por ejemplo, con valores de M para los hombres por encima y por debajo de 73.0 kg se obtendrían índices menores y mayores a 1.0 respectivamente. Cuando los valores de S se multipliquen por estos índices, el puntaje ajustado se verá mínimamente afectado cuando los valores de M estén cercanos a la media. Por otro lado, establecer un peso de referencia con un valor grande como 100 kg (donde el valor del índice se establece como 1.0), producirá desviaciones muy grandes entre Sadj y S.
El propósito de la transformación fue crear un índice por el cual S pudiera ser multiplicado de manera que los hombres con un peso mayor a 73.0 kg obtuvieran un índice “reducido” (menor a 1.0) y aquellos con un peso menor a 73.0 kg obtuvieran un índice “incrementado” (mayor a 1.0). El índice I, debe ajustarse a un valor alométrico, S.M-2/3 de la siguiente forma. El índice con un cierto valor de M y con un valor idéntico de S para los hombres debe conformar la siguiente relación (lo mismo se aplica para las mujeres, pero con un peso de referencia de 60.0 kg en lugar de 73.0):
S.M-2/3=(S.73-2/3).I (1)
La ecuación 1 ilustra que, para el mismo peso levantado, S, un sujeto de peso M, tendría su puntaje (el puntaje alométrico teóricamente y empíricamente correcto de S.M-2/3) ajustado por I. Reacomodando la ecuación y despejando I se obtiene:
I=732/3.M-2/3 (2)
RESULTADOS
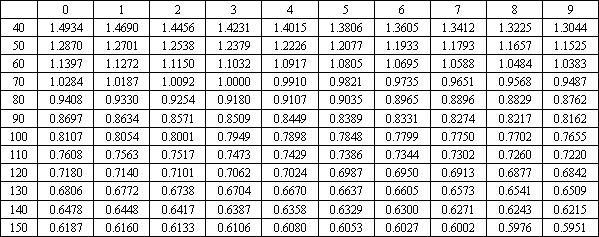
Para todos los pesos entre 40 y 150 kg, utilizando el programa Excel de Microsoft (Microsoft, Seattle, WA) se calcularon índices con incrementos de 1.0 kg, los cuales se muestran en forma de tabla (Tablas 1 y 2). Este intervalo de valores fue calculado solo para adultos y los cambios en la maduración tienden a provocar confusiones en la relación entre S y M en niños.
Tabla 1. Índice para los hombres en base a la masa corporal. La columna
de la izquierda indica la masa en unidades de 10 kg y los números de la primera
fila indican unidades de 1 kg. Por ejemplo, para un sujeto con una masa corporal
de 64 kg se tendría un índice de 1.0917.
Por ejemplo, dos hombres A y B, con valores de S de 75 y 65 kg, respectivamente, y valores de M de 65 y 55 kg respectivamente, podrían ser comparados en términos absolutos (solamente S), con un índice simple (S.M-1), o en términos del índice propuesto (Sadj, donde Sadj=S x I, donde I se saca de la tabla, en base a M). La Tabla 3 ilustra los efectos de dichas comparaciones incluyendo diferencias porcentuales (los valores indican cuanto mayor, en forma de porcentaje, es el mayor puntaje). Claramente, el método utilizado tiene un impacto significativo sobre la comparación de S entre sujetos.
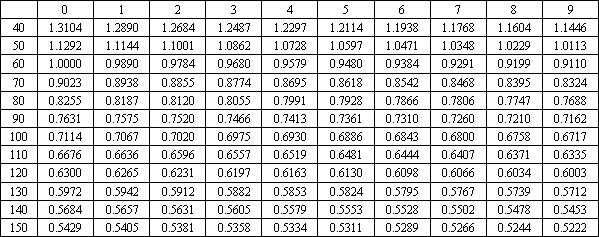
Tabla 2. Índice para las mujeres en base a la masa corporal. La columna
de la izquierda indica la masa en unidades de 10 kg y los números de la primera
fila indican unidades de 1 kg. Por ejemplo, para un sujeto con una masa corporal
de 64 kg se tendría un índice de 0.9579.
Tabla 3. Ejemplo de una comparación individual entre hombres. * Estos
valores fueron obtenidos realizando el cociente del mayor valor de la variable
dividido el menor valor, y en valor se coloca en la fila del mayor valor. El
valor de 15.4 fue obtenido de la siguiente forma: (A-B)/A; el valor de 2.60 fue
obtenido de la siguiente forma: (1.18-1.15)/1.15; el valor de 3.2 fue obtenido
de la siguiente forma: (81.0-78.50)/78.50.
DISCUSION
Las tablas de índices son en realidad nada más que una aplicación de la expresión para la fuerza ajustadas por el peso corporal, S.M-2/3. Como se discutió previamente, las unidades originales y la conversión se mantienen en la puntuación Sadj, algo que no es posible con la convención S.M-2/3 para comparaciones individuales. De este modo, las diferencias entre individuos con el Sadj o con S.M-2/3 deberían ser idénticas cuando se expresan como diferencias porcentuales.
Una limitación importante de utilizar el índice I, es la falta de apreciación acerca de cómo podrían variar los exponentes entre las distintas poblaciones. La literatura reciente está repleta de ejemplos de modelos alométricos aplicados a diferentes mediciones de la fuerza o de la potencia. La determinación de un exponente de M específico de la muestra es un proceso empírico y, por lo tanto, con frecuencia se producen exponentes distintos del 2/3 esperado. De esta manera, uno podría sospechar que el uso “arbitrario” y generalizado del exponente 2/3 como se sugiere en este artículo llevaría a situaciones en donde M no es totalmente tomado en cuenta cuando se comparan grupos o individuos. Por lo tanto se puede argumentar que dicho ajuste debería ser específico de la muestra y solo debería servir como una especie de análisis de covarianza. Sin embargo, deben considerarse dos puntos clave. Primero, aunque se han reportado muchos exponentes diferentes, todos contienen un intervalo de confianza del 95% dentro del cual se encuentran todos los exponentes adecuados, asumiendo características favorables de distribución de la muestra (lo que significa que la utilización de cualquiera de los exponentes produciría correlaciones entre S.M-a y S distintas de cero, una condición necesaria para una expresión apropiada del índice). Como se mencionó previamente, cuando se consideran todos los factores de confusión tales como el nivel de entrenamiento, la grasa corporal, y el estadio puberal, la mayoría de los estudios reportan intervalos de confianza que contienen el valor de 2/3. Segundo, en los mismos intervalos de confianza no se ha hallado el valor de “1” (fortaleciendo de esta manera el argumento de no utilizar el método del cociente). Tercero, la utilización de diferentes exponentes específicos de la muestra puede ser bastante problemática, ya que cada uno produce unidades diferentes por lo que la interpretación se vuelva aun más difícil. En conclusión, se podría decir que, si bien el valor de 2/3 para el exponente de la masa corporal para el ajuste de S, no es perfecto, es probablemente la mejor técnica de ajuste.
Se necesitan más investigaciones para estudiar como las mediciones isocinéticas e isotónicas de la fuerza pueden ajustarse con distintas dimensiones corporales [More research is needed to investigate how isokinetic and isotonic measures of strength scale by various body dimensions]. Aunque las contribuciones de los factores neurales, biomecánicos y fisiológicos pueden tender a confundir la simple teoría que subyace al exponente 2/3, se podría sugerir que estos factores solo son importantes en mediciones isométricas y con resistencia variables de la fuerza. Debido a que el exponente de 2/3 para la masa corporal ha sido validado empíricamente para estas últimas mediciones de la fuerza, entonces la utilización de las Tablas 1 y 2 para mediciones isocinéticas e isotónicas parece prudente para realizar comparaciones de rutina de la fuerza entre individuos.
La única advertencia que vale la pena repetir es que los índices simples propuestos en este artículo son más útiles y apropiados para comparaciones individuales, pero no para comparaciones grupales, para las cuales es conveniente la realización de algún tipo de análisis de covarianza.
En conclusión, debido a que el nuevo índice, I (en base al exponente de 2/3 para M), parece tener respaldo tanto teórico como empírico y a que probablemente es superior a los estándares calculados con simples cocientes, este puede ser ampliamente utilizado para realizar comparaciones individuales de S ajustada por M. Las tablas de índices adjuntas proporcionan un forma más simple (aunque matemáticamente equivalente) para basar las comparaciones individuales en el exponente 2/3 de M en relación a las mediciones de S.
Dirección para el envío de correspondencia
Paul M. Vanderburgh, Ph.D., HSS Dept., University of Dayton, Dayton, OH 45469-1210, Tel: 937.229.3997, Fax: 937.229.4244, correo electrónico: [email protected] Página Principal: http://homepages.udayton.edu/~vanderbu
REFERENCIAS
1. Astrand PO, Rodahl K (1986). Textbook of Work Physiology (3rd Ed). 399-405. New York: McGraw Hill
2. Lietzke MH (1956). Relation between weight-lifting totals and body weight. Science; 124: 486-487
3. Vanderburgh, PM, Mahar MT, Chou CH (1995). Allometric scaling of grip strength by body mass in college-age men and women. Res Q Exerc Sport; 66: 80-84
4. Vanderburgh PM, Sharp M, Nindl B (1998). Nonparallel slopes using analysis of covariance for body size adjustment may reflect inappropriate modeling. Meas Phys Ed Exerc Sci; 2: 127-135
5. Vanderburgh PM, Dooman C (1996). Considering body mass differences, who are the strongest women in the world?. Med Sci Sports Exerc. In press
6. Vanderburgh PM, Batterham AM (2000). Validation of the Wilks powerlifting formula. Med Sci Sports Exerc. In press
7. Batterham AM, George KP (1997). Allometric modeling does not determine a dimensionless power function ratio for maximal muscular function. J Appl Physiol; 83: 2158-2166
8. Croucher JS (1984). An analysis of world weightlifting records. Res Q Exerc Sport; 285-288
9. Bancroft GA, Biddle SJ, Brown SC (1987). Handicapping formulae in Olympic weightlifting: a reappraisal for schoolboy weightlifters. Res Q Exerc Sport; 58:388-391
10. Hui, SC, Mahar MT, Jackson AS (1995). Adjusting upper body strength by body mass using allometric scaling. Med Sci Sports Exerc; 27: S211
11. Wilkes R (1998). Wilkes formula for men and women. http://www.ipf.com/formula.htm
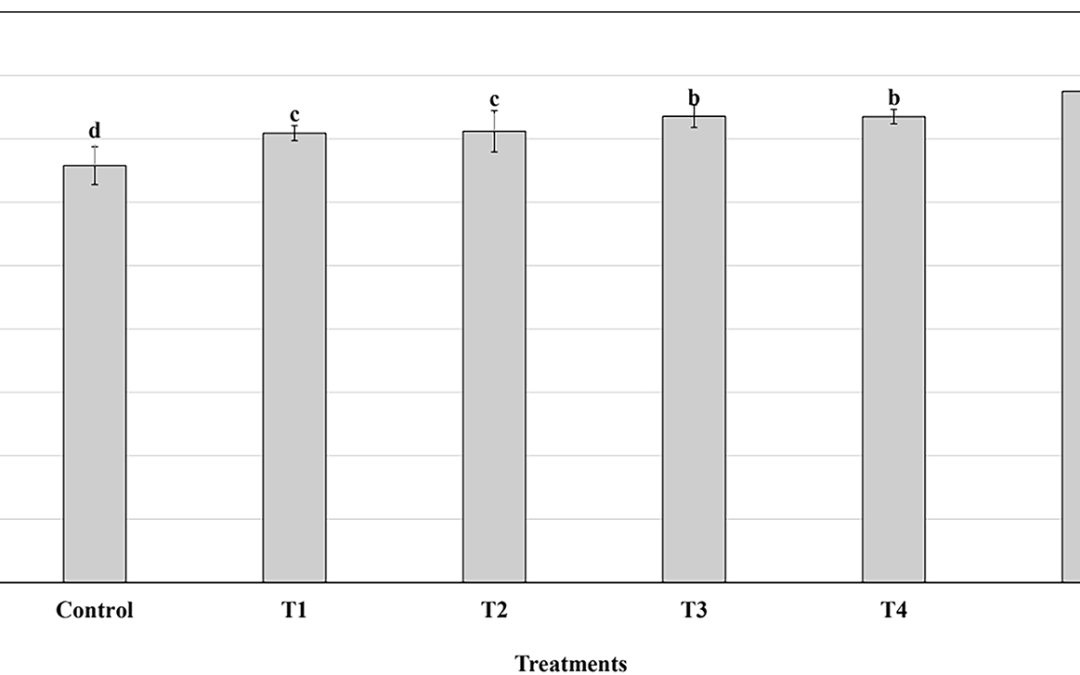
Mejora de las propiedades nutricionales y de textura del jerky reestructurado con polvo de sangre de pato para aplicaciones en kits de comida
Resumen del Estudio sobre el Uso de Polvo de Sangre de Pato en Jerky Reestructurado En un contexto...
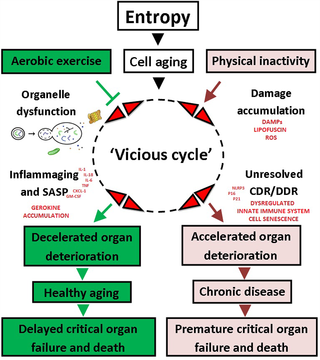
El ejercicio aeróbico a lo largo de la vida protege contra la inflamaging y el cáncer
Ejercicio Aeróbico y su Impacto en el Envejecimiento y el Riesgo de Cáncer La investigación...
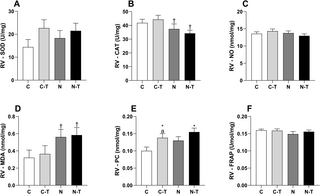
La combinación de nandrolona y entrenamiento de resistencia indujo remodelación cardíaca y estrés oxidativo a pesar de la contractilidad mejorada de los cardiomiocitos
Este artículo investiga cómo la combinación de entrenamiento de resistencia (RT) y el uso de...
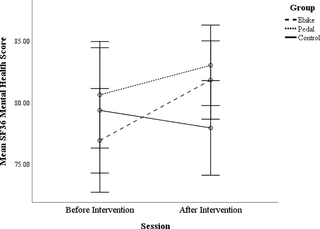
El efecto del ciclismo en la función cognitiva y el bienestar en adultos mayores
El impacto del ciclismo al aire libre en la función cognitiva y bienestar de los adultos mayores...
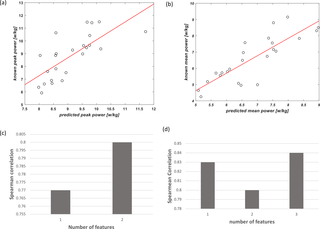
Predicción de las salidas de potencia mecánica anaeróbica del Wingate a partir de una prueba de esfuerzo cardiopulmonar incremental máxima utilizando un enfoque de aprendizaje automático
El Wingate Anaerobic Test (WAnT) se ha establecido como un método efectivo para medir la potencia...