1Department of Physical Education, Catholic University of Brasilia, Brasilia, DF, Brazil.
2Exercise Physiology Laboratories, Exercise Science Program, Department of Phsysical Performance and Development, The University of New Mexico, Albuquerque, New Mexico 87131.
3Exercise and Sport Science Department, Vanguard University of Southern California, Costa Mesa, CA, USA.
Resumen
INTRODUCCIÓN
Ya que el rendimiento atlético está parcialmente influenciado por la relación entre la propia masa grasa (FM) y la masa magra (FFM), muchos atletas se interesan por su composición corporal. Sin embargo, el interés sobre el propio porcentaje de grasa corporal (% BF) no debería estar limitado solo a los atletas. Una precisa medición de la composición corporal individual es importante para todos los individuos, por ejemplo % BF está estrechamente relacionado a la salud y el bienestar individual. De acuerdo al Colegio Americano de Medicina del Deporte (American Collage of Sport Medicine) (1), la obesidad está asociada a un riesgo incrementado para el desarrollo de enfermedad cardiovascular, hipertensión, diabetes, tipos específicos de cáncer y otras enfermedades crónicas. Además, existe evidencia que en poblaciones que experimentan rápidos cambios culturales y cambios en el estilo de vida, los individuos pueden ser más vulnerables al desarrollo de alto niveles de adiposidad y de sus complicaciones (2). Los cambios culturales en países como Brasil pueden predecir cambios fisiológicos con grandes implicancias para la salud pública. El Instituto Nacional Brasilero de Nutrición (3) ha reportado que cerca de siete millones de adultos son obesos, lo cual significa que el número de obesos se ha duplicado durante los últimos 15 años.
Tradicionalmente, el clásico modelo de dos componentes (4, 5), que separa la masa corporal total en FM y FFM, ha sido utilizado para obtener mediciones de referencia acerca de la composición corporal. Este modelo se basa en la indudable presuntuosidad sobre las densidades de los tejidos y las distribuciones relativas de agua, proteínas, y minerales en la masa magra.
Las proporciones de agua, proteínas y minerales en la masa magra, y por ello la densidad global de la masa magra (FFBd) varía con la edad, sexo, etnia, nivel de grasa corporal y nivel de actividad física (6, 8). La variación real de la supuesta medición de FFBd puede resultar en un error sistemático al estimar el % BF. Por ello, mientras el modelo de dos componentes provee estimaciones precisas del % BF en hombres blancos, a partir de los cuales esta suposición fue derivada, este modelo no debería ser conveniente para el uso en subgrupos de poblaciones donde la FFBd varía del valor asumido.
La etnia es una de las características de los subgrupos que puede violar la presuntuosidad del modelo de dos componentes. Por ejemplo, la FFBd de la mujer negra (1.106 g/cm3) y de la mujer hispana (1.105 g/cm3) son mayores al valor adoptado de 1.100g/cm3debido a su mayor contenido mineral óseo relativo (9, 11). Por lo tanto, los expertos en el campo de la composición corporal (12, 13) recomiendan utilizar ecuaciones de predicción solo después que han sido validadas para un subgrupo de población específico. La mayoría de las ecuaciones de predicción de la composición corporal utilizadas hoy en día han sido desarrolladas para la población norteamericana descendiente de europeos. Estas ecuaciones pueden carecer de validez en la predicción para poblaciones de otras etnias u orígenes raciales. Estos subgrupos no están tan bien definidos. Por ejemplo, muchos brasileños son una mezcla de ancestros europeos, africanos y de aborígenes americanos, y por ello son una homogénea amalgamación de tres continentes (14).
En Brasil, se han utilizado ecuaciones de predicción generalizada de pliegues cutáneos (SKF) para estimar la densidad corporal (Db) (15, 16). Sin embargo, estas ecuaciones de predicción no han sido validadas para mujeres y hombres brasileros. Existe una necesidad de validar las ecuaciones de predicción de composición corporal existentes para determinar su aplicación a la población brasilera. Por ello, este estudio fue conducido para determinar la aplicabilidad y la precisión predictiva del método de campo de pliegues cutáneos y seleccionar ecuaciones de predicción para la estimación de la composición corporal de mujeres brasileras.
MÉTODOS
Sujetos
Este estudio fue aprobado por los Comités de Revisión de la Universidad de Nuevo México, Albuquerque, Nuevo México, USA y de la Universidad Católica de Brasil. Cuarenta y cuatro mujeres del área de Brasilia, de entre 20 y 40 años, participaron voluntariamente del estudio. Las mujeres que respondieron a los volantes distribuidos en centros de salud, clubes sociales, oficinas públicas, y a través del boca a boca fueron seleccionadas aleatoriamente. Las mujeres fueron informadas de los propósitos, procedimientos, posibles molestias, riesgos, y beneficios del estudio previo a la entrega del informe de consentimiento escrito.
Para reunir datos descriptivos y para definir el ciclo menstrual de las participantes fueron usados cuestionarios sobre historia de la salud y la actividad física (17). Las mujeres que experimentaron retención de agua durante el ciclo menstrual fueron listadas para ser evaluadas en el momento en el que ellas percibían que se encontraban en su peso corporal usual. Por ello fueron minimizados los efectos de la retención de agua sobre el peso corporal y la Db (18). Las participantes eran excluidas del estudio, si no habían sido eumenorreicas durante el año previo al estudio. También fueron investigados los antecedentes médicos de las mujeres que podrían alterar la composición corporal. Las contraindicaciones incluyeron cáncer, hipertensión, enfermedades cardiovasculares, enfermedades renales y hepáticas, y distrofias musculares.
Lugar
Todos las evaluaciones fueron conducidos en la Clínica de Endocrinología y Metabolismo en Brasilia, Brasil.
Procedimientos
Se les instruyó a las mujeres no comer dentro de las 4 horas, no tomar alcohol dentro de las 48 hs., y no realizar ejercicios dentro de las 12 horas previas a la llegada a la clínica. A la llegada, todos los participantes dieron su informe de consentimiento escrito y llenaron los cuestionarios. Después se sometieron a las siguientes evaluaciones en el orden indicado: talla (HT), peso corporal (BM), medición de los pliegues cutáneos, y absorciometría dual por energía de rayos X (DXA). Luego de las evaluaciones las participantes recibieron interpretaciones orales y escritas de los resultados.
Talla y Peso Corporal
La HT y la BM fueron medidos con las participantes descalzas, vistiendo shorts y remera. La BM fue medida con una aproximación de 0.1 kg sobre una balanza electrónica médica. (Filizzola, Sao Paulo, SP, Brasil). La HT fue medida con una aproximación de 0.1 cm en la mitad de una inspiración utilizando un estadiometro montado sobre la pared (Accustat, Ross Laboratories, Columbus OH) mientras los sujetos permanecían erectos con los brazos relajados al costado del cuerpo. Fue registrada la media de dos mediciones.
Método de Pliegues Cutáneos (SKF)
Un calibre Lange para SKF (Cambridge Scientific Industries, Cambridge, MD) fue utilizado para medir el espesor de los SKF con una aproximación de 0.5 mm. Los sitios para la medición de SKF fueron marcados con un lápiz quirúrgico de marcación. Todos los pliegues cutáneos fueron tomados sobre el lado derecho del cuerpo, y el mismo técnico tomo un mínimo de dos mediciones en cada sitio en un orden rotatorio. El promedio de dos mediciones dentro del 10% de cada una fue registrado como el grosor del SKF para ese sitio.
Las mediciones de SKF fueron usadas para validar las ecuaciones de Jackson y cols. (16) de sumatoria de 3 (∑3SKF) y 7 (∑7SKF) pliegues cutáneos. Como describieron Jackson y Pollock (20) los siguientes sitios fueron medidos: pecho, axilar medial, triceps, subescapular, abdominal, suprailíaco, y muslo.
Absorciometría Dual por Energía de Rayos X
La grasa corporal total, tejidos blandos libres de grasa, y las mediciones de densidad mineral ósea fueron obtenidas con un scanner de cuerpo completo Lunar DPX-IQ (Lunar Radiation Corporation, Madison, WI, U.S.A., software versión 4.6 A). El DXA fue calibrado previo a las evaluaciones con marcadores de calibración conocidos, de acuerdo a la guía del fabricante. La exploración de todo el cuerpo tomo entre 10 y 20 minutos, dependiendo del tamaño del participante. Vestidos completamente sin ningún metal cada participante permaneció inmóvil en la posición supina con los brazos al costado del cuerpo durante todo la exploración. La radiación total fue 0.1 µG, lo cual es equivalente a 1/20 del promedio de un rayo-X dental. La medida del % BF se basó sobre una extrapolación de la adiposidad a partir del cociente de atenuación de tejidos blandos de la energía de dos rayos-X, en los píxeles que no contenían hueso (21).
El DXA fue utilizado para obtener una medida de referencia del % BF en este estudio. Los investigadores han encontrado anteriormente una buena concordancia entre el % BF estimado con DXA y el obtenido a partir modelos de composición corporal multicomponentes (22-25). Estos mismos investigadores (20-23) concluyeron que el DXA fue mejor predictor del % BF que otros métodos de referencia, como el pesaje hidrostático y la dilución de isótopos, utilizados en conjunción con los modelos de dos componentes.
Análisis Estadístico
Fueron utilizados análisis de regresión [Paquete Estadístico para Ciencias Sociales (SPSS 8.0)] para medir la precisión predictiva de la ecuación de Jackson y cols. (16) generalizados para ∑3SKF y ∑7SKF, utilizando la fórmula de Siri (5) y la fórmula de Heyward y Stolarczyk (12) para convertir la Db en % BF. Se asume a partir los análisis de regresión, que tanto las variables independientes, como las variables dependientes, están normalmente distribuidas. Si no se excluyen del análisis los casos extremos, pueden elevar, ya sea, el error de estimación estándar (SEE), y los coeficientes de correlación múltiple (26). Por esta razón, los casos extremos univariados fueron identificados y removidos de los análisis subsecuentes. Los casos extremos univariados fueron definidos como un exceso en la puntución Z, mayor de 3.29 desvíos estándar de la media para esa variable (>Z ±3.29 de la media) (26).
Cada ecuación SKF fue evaluada usando el criterio de validación desarrollado por Lohman (13). Las medias y los desvíos estándar de FFM y % BF del método de referencia (DXA) y de la predicción de FFM y % BF de cada ecuación de predicción fueron comparadas usando un test-t dependiente. Fueron examinados la correlación entre la referencia y la predicción de % BF (ry, y’), r2, y SEE, así como la correlación entre el % BF de referencia y los puntajes residuales para todos los sujetos (ry, res) (26). Los puntajes residuales fueron calculados para cada participante mediante la substracción del %BF de la respectiva medición de referencia. Los mismos fueron analizados utilizando una variación del método de Bland y Altman (28) para determinar el porcentaje de participantes cuyo %BF fue correctamente estimado dentro de ± 3,5 % BF.
Adicionalmente, se determinaron las pendientes y las intercepciónes para la recta que mejor se acomodaban, para cada ecuación. Cada pendiente fue evaluada para determinar cuando hubo una diferencia estadísticamente significativa a partir de 1.0 (p<0.05). Cada intercepción fue evaluada para determinar cuando hubo una diferencia estadísticamente diferente de cero (p<0.05). Además, se hizo un intento para reducir las amenazas a la validez externa, a través de la selección de mujeres del área de Brasilia. En el 2000, la población de Brasilia era de aproximadamente 2.0 millones de habitantes (19). Con el nacimiento de Brasilia en 1960, personas de todas las regiones, edades, y rangos socioeconómicos del Brasil se mudaron a la ciudad. “Brasilia, localizada en el estado de Goias, se convirtió en el símbolo de la unificación de todas la regiones de Brasil” (14). Por ello, Brasilia es la ciudad que probablemente mejor representa la población Brasilera.
RESULTADOS
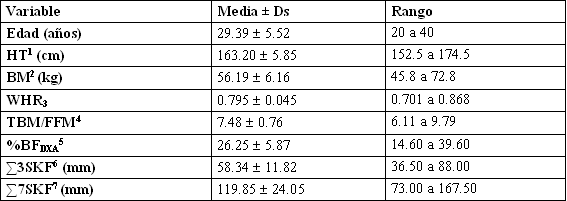
Las características físicas de los participantes (n =44) son presentadas en la Tabla 1. Las revisiones iniciales de los datos, revelaron que las variables estuvieron normalmente distribuidas, y no se hallaron casos extremos (Z >±3.29). Por ello, todos los sujetos fueron incluidos en los análisis subsecuentes.
Tabla 1. Características físicas de la muestra (n =44); 1 HT, talla; 2 BM, masa corporal; 3 WHR, cociente cintura cadera; 4 TBM/FFM,
mineral óseo total relativo a la masa magra; 5 % BFDXA, grasa corporal relativa a
la masa corporal obtenida por absorciometría dual por energía de rayos X; 6
∑3SKF, sumatoria de 3 pliegues cutáneos; 7 ∑7SKF, sumatoria de 7 pliegues
cutáneos.
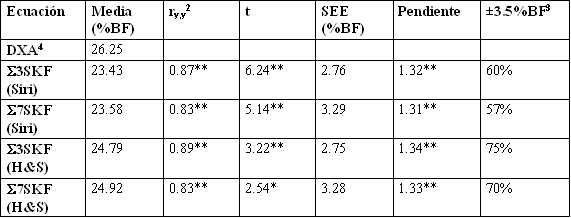
Los resultados de los análisis de la validación de las ecuaciones de predicción de pliegues cutáneos son presentados en la Tabla 2. El % BF estimado por la ecuación de sumatoria de 3 pliegues cutáneos.
(∑3SKF ) de Jackson y cols. (16) fue obtenido inicialmente, utilizando el modelo de conversión de Db a % BF de dos componentes, propuesto por Siri (5). Esta estimación fue comparada con el % BF obtenido del método de referencia DXA. La relación entre la referencia y el % BF estimado por la ecuación de ∑3SKF es presentada en la Figura 1. El SEE para cada ecuación fue aceptable, sin exceder el criterio de 3.5 % BF (13). Sin embargo, en esta muestra las ecuaciones de sumatoria de 3 (∑3SKF) y 7 (∑7SKF) pliegues cutáneos, subestimaron significativamente (p<0.01) el promedio del % BFDXA en 2.82 % BF y 2.67 % BF, respectivamente. Además, aunque las intercepciones de las ecuaciones no difirieron significativamente de cero, las pendientes fueron significativamente diferente de uno (p<0.05).
Las correlaciones entre los puntajes residuales (% BFDXA– % BFSKF) y el promedio de ambos métodos (% BFDXA + % BFSKF /2) fueron significativamente diferentes de las ecuaciones de ∑3SKF y ∑7SKF (ry,res =0.79 y 0.80, respectivamente, p<0.01), indicando que estas ecuaciones tendieron a sobreestimar sistemáticamente el % BF en las mujeres mas magras y a subestimar el % BF en las mujeres con mayor adiposidad (Figura 2). Además, el % BF de los individuos fue precisamente estimado dentro de ± 3.5 de % BF para menos de las dos terceras partes de la muestra (60% para ∑3SKF y 57% para ∑7SKF).
Tabla 2. Validación de la ecuación1 de SKF de Jackson y cols. (14) en mujeres
brasileras (n =44)
1 ∑3SKF, sumatoria de 3 pliegues cutáneos; ∑7SKF, sumatoria de 7 pliegues
cutáneos; Siri, conversión de la fórmula de Siri (5); H&S, fórmula de conversión
para población específica de mujeres hispanas de Heyward y Stolarczyk (12);2
ry,y’, correlación entre la referencia y la predicción del porcentaje de grasa;
3 ± 3.5% BF, porcentaje de los sujetos a quienes se les estimó precisamente la
grasa corporal dentro de ± 3.5 %; 4 DXA, absorciometría dual por energía de
rayos-X * P<0.05; ** P<0.01
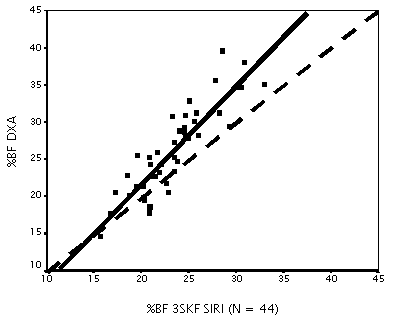
Figura 1. Relación entre la grasa corporal relativa (% BF) medida por DXA y la
estimada por ∑3SKF. El %BF fue estimado utilizando la fórmula de
conversión de Siri (5). La recta punteada es la línea de identidad, y la recta sólida es
la recta de regresión.
Figura 2. Análisis de los valores residuales de % BF para ∑3 SKF utilizando la
fórmula de conversión de Siri (5). Un SEE dentro de ± 3.5% BF es considerado
“bueno” cuando se evalúa la precisión de la predicción de las mediciones del %BF
(13).
DISCUSIÓN
Las ecuaciones de predicción SKF examinadas mediante validación en este estudio fueron las de ∑3SKF y ∑7SKF desarrolladas por Jackson y cols. (16). Cuando se comparó al % BFDXA, el promedio de % BF obtenido a partir de las dos ecuaciones de SKF, fue significativamente subestimado. Sin embargo, Heyward y Stolarczyk (12) sugirieron que el método SKF no debería ser usado para medir la composición corporal en individuos obesos. Por ello, también fue realizado un análisis separado para evaluar la validez de las ecuaciones de SKF solo en la submuestra (n =32) de las mujeres no obesas de este estudio (< 30 %BF). Los resultados de estos análisis indicaron que el promedio de la diferencia entre % BFDXA y % BFSKF fue reducido de 2.82 % BF y 2.67 % BF a 1.67 % BF y 1.2 % BF, respectivamente para las ecuaciones de ∑3SKF y ∑7SKF. Aunque estas diferencias fueron pequeñas, siguieron siendo estadísticamente significativas (p<0.05).
La tendencia de las ecuaciones de ∑3SKF y ∑7SKF a subestimar sistemáticamente el % BF en mujeres brasileras puede ser explicado, en parte, mediante un examen del mineral corporal total relativo de esta muestra. Stolarczyk y cols. (11) midieron la composición corporal de mujeres hispanas jóvenes (20-39 años) (n =29) y reportaron que su promedio en el mineral corporal total relativo es 7.4% de la FFM. El mineral corporal relativo de la mujer brasilera en este estudio (7.48 FFM) fue similar al reportado por Stolarczyk y cols. (11). Este valor es mayor al asumido (6.48 %FFM) por el modelo de dos componentes de Siri (5). Por ello la FFBd general de las mujeres brasileras premenopáusicas fue también superior al valor asumido (1.100 g/cm3), por ello se produjo una subestimación sistemática del % BFDXA cuando el modelo de dos componentes de Siri (5) fue usado para convertir la Db a % BF.
Basados en los hallazgos de Stolarczyk y cols (11), Heyward y Stolarczyk (10) desarrollaron una fórmula de conversión del modelo de dos componentes para una población específica para estimar el % BF a partir de la Db en mujeres hispanas: % BF =4.87/ Db- 4.41. Esta fórmula asume una FFBd de 1.105 g/cm3. Los autores recomendaron utilizar esta fórmula para estimar el %BF desde la medición hidrostática de Db, tanto como de la Db predecida por las ecuaciones de ∑SKF de Jackson. Por ello, la precisión predictiva de esta fórmula de conversión para una población específica fue evaluada para la muestra total (n = 44) en el presente estudio. Las diferencias medias (% BFDXA vs % BFSKF) fueron reducidas desde 2.82 % BF y 2.67 %BF obtenidas de la fórmula de conversión de Siri (5) a 1.46 %BF y 1.33 % BF para las ecuaciones de ∑3SKF y ∑7SKF, respectivamente; sin embargo estas diferencias permanecieron siendo estadísticamente significativas (P<0.05). También, el error de predicción (SEE) para cada ecuación no cambió significativamente del análisis original que utilizó la fórmula de conversión de Siri (5) (Tabla 2).
Tabla 3. Validación de las ecuaciones1 de SKF de Jackson y cols. (16)
utilizando una fórmula de conversión de densidad corporal específica para la
población (12) en la submuestra (n =32) de mujeres brasileras no obesas (< 30%
de grasa) ; 1∑3SKF sumatoria de 3 pliegues cutáneos; ∑7SKF sumatoria de 7 pliegues
cutáneos ; 2ry y correlación entre la referencia y el porcentaje de grasa predecido
; 3 ±3.5% porcentaje de sujetos a quienes se les estimó con precisión el % BF ; 4 DXA absorciometria dual por energía de rayos X
; *p<0.05; **p<0.01
Figura 3. Relación entre la grasa corporal relativa (% BF) medida con DXA y la
estimada con ∑3 SKF utilizando una submuestra de mujeres no obesas. El % BF
fue estimado usando la fórmula de conversión hispánica (12). La línea punteada es la
línea de identidad, la línea sólida es la recta de regresión
Figura 4. Análisis de los valores residuales de % BF para ∑3 SKF en mujeres no
obesas utilizando la fórmula de conversión hispánica (12). Un SEE dentro de ±
3.5 % BF es considerado “ bueno” cuando se evalúa la precisión de la predicción de
la medición del % BF (13).
Sin embargo cuando se aplicó la fórmula de conversión para la mujer hispana (12), solo a la submuestra de mujeres no obesas (n =32), cada criterio de validación fue hallado (Tabla 3). La relación entre la referencia y el % BF predecido por la ecuación de ∑3SKF aplicada a la submuestra de mujeres no obesas se muestra en la figura 3. Las diferencias entre el promedio del % BFDXA y el % BF estimado por las ecuaciones ∑3SKF (0.29 % BF) y ∑7SKF (0.17 % BF) fueron pequeñas y no significativas. Además, cerca de todas las participantes (87%) fueron precisamente estimadas en % BF ± 3.5 % para las ecuaciones de ∑3SKF y ∑7SKF (Figura 4).
Basados en estos hallazgos, aparentemente las ecuaciones de ∑3SKF y ∑7SKF, de Jackson y cols. (16) producen una estimación precisa del % BF en mujeres saludables, no obesas, brasileras cuando estas ecuaciones de SKF son usadas junto a una fórmula de conversión para una población específica de mujeres hispanas (12). Aunque ambas ecuaciones de SKF pueden ser utilizadas, la ∑3SKF es más práctica dado a que requiere la medición sólo de tres sitios de SKF comparados a los siete sitios de la otra ecuación. Sin embrago, los resultados del presente estudio indicaron que estas ecuaciones de SKF no deberían ser usadas para la medición de la composición corporal de mujeres brasileras obesas (>30 % BF). Por ello, se necesita que se realicen estudios futuros con el objeto de explorar como la adiposidad y la distribución de la grasa afectan la precisión de la predicción de otros métodos de campo para la medición de la composición corporal, especialmente el método de bioimpedancia.
Agradecimientos: Agradecemos al Dr. Joao Lindolfo de la Clínica de Endocrinología y Metabolismo de Brasilia, Brasil por el uso de la unidad DEXA. Este estudio fue financiado en parte por CAPES/BRASIL.
REFERENCIAS
1. American College of Sports Medicine (2000). ACSMs guidelines for exercise testing and prescription. 6th ed. Media, PA: Williams & Wilkins, 214
2. Seidell, CJ (1996). Relationship of total and regional body composition to morbidity and mortality. In A. F. Roche, S. B. Heymsfield & T. G. Lohman. Human body composition. Champaign, IL: Human Kinetics, 345-353
3. INAN / Brazilian National Institute of Nutrition (1991). Condicoes nutricionais da populacao brasileira: adultos and idosos, [Nutritional conditions of Brazilian population: adult and elderly]. Ministerio da Saude / INAN
4. Brozek J, Grande F, Anderson JT, Keys A (1963). Densitometric analysis of body composition: revision of some quantitative assumptions. Ann N Y Acad Sci; 110: 113-40
5. Siri WE (1961). Body composition from fluid spaces and density: analysis of methods. In: Brozek J, Henschel A, eds. Techniques for measuring body composition. Washington, DC: National Academy of Sciences, 223-44
6. Baumgartner RN, Heymsfield SB, Lichtman S, Wang J, Pierson, RN (1991). Body composition in elderly people: effect of criterion estimates on predictive equations. Am J Clin Nutr; 53: 1345-53
7. Wang J, Heymsfield SB, Aulet M, Thornton JC, Pierson RN (1989). Body fat from body density: underwater weighing vs. dual-photon absorptiometry. Am J Physiol; 256: E829-34
8. Williams DF, Going SB, Massett MP, Lohman TG, Bare LA, Hewitt MJ (1993). Aqueous and mineral fractions of the fat-free body and their relation to body fat estimates in men and women aged 49-82 years. In: Ellis KJ, Eastman JD, eds. Human body composition: in vivo methods, models and assessment. New York, NY: Plenum Press, 109-113
9. Cote K, Adams WC (1993). Effect of bone density on body composition estimates in young adult black and white women. Med Sci Sports Exerc; 25: 290-6
10. Ortiz O, Russell M, Daley TL, et al (1992). Differences in skeletal muscle and bone mineral mass between black and white females and their relevance to estimates of body composition. Am J Clin Nutr; 55: 8-13
11. Stolarczyk LM, Heyward VH, Goodman JA, et al (1995). Predictive accuracy of bioimpedance equations in estimating fat-free mass of Hispanic women. Med Sci Sports Exerc; 10: 1450-6
12. Heyward VH, Stolarczyk LM (1996). Applied body composition assessment. Champaign, IL: Human Kinetics, 2-20
13. Lohman TG (1992). Advances in body composition assessment. Champaign, IL: Human Kinetics, 3-4,44
14. Burns BE (1980). A history of Brazil. New York: Columbia University Press, 56
15. Jackson AS, Pollock ML (1978). Generalized equations for predicting body density of men. Br J Nutr; 40: 497-504
16. Jackson AS, Pollock ML, Ward A (1980). Generalized equations for predicting body density of women. Med Sci Sports Exerc; 12: 175-82
17. Ross RM, Jackson AS (1990). Exercise concepts, calculations, and computer applications. Carmel, IN: Benchmark, 109
18. Bunt SC, Lohman TG, Boileau RA (1989). Impact of total body water fluctuations on estimation of body fat from body density. Med Sci Sports Exerc; 21: 96-100
19. IBGE/ Fundacao Instituto Brasileiro de Geografia e Estatistica (2000). Censo Demografico [Demographic Census, 2000]. Brasilia, DF, 43
20. Jackson AS, Pollock ML (1985). Practical assessment of body composition. Physician Sportsmed; 13: 76-90
21. Mazess RB, Barden HS, Bisek JP, Hanson J (1990). Dual-energy-ray absorptiometry for total body and regional bone-mineral and soft-tissue composition. Am J Clin Nutr; 51: 1106-12
22. Friedl KE, DeLuca JP, Marchitelli LJ, Vogel JA (1940). Reliability of body-fat estimations from a four-component model by using density, body water, and bone mineral measurements. Am J Clin Nutr; 55: 764-70
23. Fuller NJ, Jebb SA, Laskey MA, Coward WA, Elia M (1992). Four-component model for the assessment of body composition in humans: comparison with alternative methods and evaluation of the density and hydration of fat-free mass. Clin Sci (Colch); 82: 687-93
24. Prior BM, Cureton KJ, Modlesky CM, et al (1997). In vivo validation of whole body composition estimates from dual-energy X-ray absorptiometry. J Appl Physiol; 83: 623-30
25. Wagner DR, Heyward VH (2001). Validity of two-component models for estimating body fat of black men. J Appl Physiol; 90: 649-56
26. Tabachnik BG, Fidell LS (1996). Using multivariate statistics. New York: Harper Collins,66-68
27. Lohman TG (1981). Skinfold and body density and their relation to body fatness: a review. Am J Hum Biol; 53: 181-225
28. Bland JM, Altman DG (1986). Statistical methods for assessing agreement between two methods of clinical measurements. Lancet, 12: 307-10
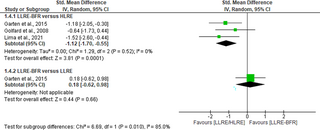
Efecto agudo del ejercicio de resistencia de baja carga con restricción del flujo sanguíneo sobre los biomarcadores de estrés oxidativo: una revisión sistemática y un metanálisis
Resumen Fondo El propósito de esta revisión fue analizar los efectos agudos del ejercicio de...

Efectos del entrenamiento de swing con pesas rusas sobre la demanda cardiorrespiratoria y metabólica en una competición simulada en jóvenes gimnastas artísticas
ResumenExaminamos los efectos de agregar un programa de entrenamiento de Kettlebell Swing (KB) al...
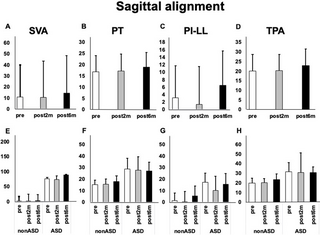
Efectos y limitaciones del ejercicio de control motor en el hogar para el dolor lumbar crónico: un estudio prospectivo de un solo centro
Resumen Diseño del estudio Estudio observacional prospectivo unicéntrico. Objetivo Investigar los...
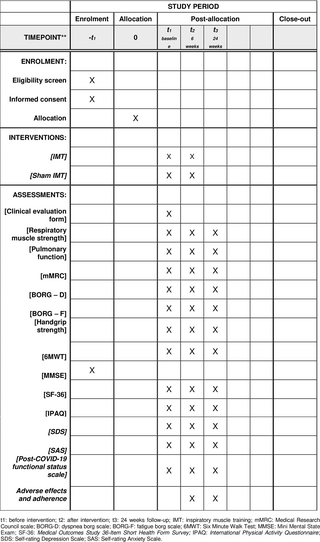
Eficacia del entrenamiento de los músculos inspiratorios domiciliario en pacientes post-covid-19: protocolo para un ensayo clínico aleatorizado
Resumen Introducción La evidencia actual sugiere la aparición de un nuevo síndrome (síndrome de...

Estimación de la carga relativa a partir de la velocidad del movimiento en el ejercicio de press de pecho sentado en adultos mayores
Resumen Apuntar Este estudio tuvo como objetivo i) determinar la relación carga-velocidad en el...